在前面几篇中分类问题和回归问题里涉及到的伯努利分布和高斯分布都是广义线性模型(Generative Linear Models.GLMs)的特例。下面将详细介绍广义线性模型。
1、指数族
我们可以将一些分布总结到一个指数族中。指数族可表示为:
η是指naturalparameter/canonical parameter,T (y)是指sufficientstatistic, a(η)是指logpartition function。T、a和b的选择决定了分布族,η的改变会得到这个分布族里的不同分布函数。
伯努利分布和高斯分布都是指数族分布的例子。首先伯努利分布可以如下表示:
因此可以得到以下结果:
这表明伯努利分布可以通过选择适当的T、a和b用指数族的形式表示。其次高斯分布可表示为:
同理可得以下结果:
2、构建广义线性模型
一般针对一个问题要用到广义线性模型,我们基本都遵循以下三个假设。
(1)y | x; θ ∼ ExponentialFamily(η).先根据数据假设y服从某一指数族分布。
(2)选择一个假设函数满足h(x) =E[y|x]。根据这个,我们可以预测x对应的y值或者进行分类。
(3)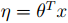
下面将通过最小二乘法和Logistic回归熟悉构建广义线性模型的步骤。
2.1 最小二乘法
最小二乘法针对的是连续型的数值。y满足高斯分布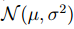
2.2 Logistic回归
伯努利分布是针对二元分类问题的指数族分布。y|x; θ ∼ Bernoulli(φ),从1、指数族中的分析可以知道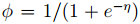
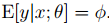
3、Softmax回归
当分类问题不再是二元而是k元的时候,即y∈{1,2,…,k}。我们可以利用构建广义线性模型来解决这个分类问题。具体步骤如下。
假设y服从指数族分布,φi = p(y = i; φ)并且可知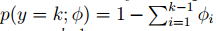
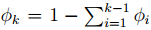

此外1{·}代表括弧里的条件为真式整个式子的值为1,否则为0。所以(T (y))i = 1{y = i}。从概率论的知识可知,E[(T (y))i] = P (y = i) = φi 。所以我们可以得到:
所以
所以
定义ηk =log(φk/φk) = 0,所以
所以
所以softmax函数可以如下表示:
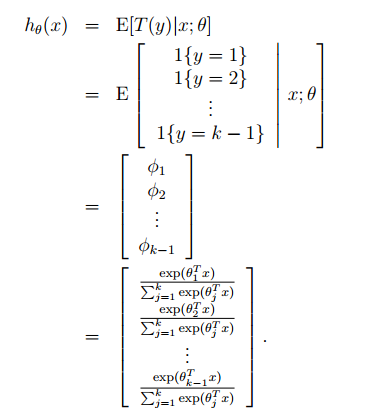
根据假设(3),并定义θk = 0,所以可以得到Softmax回归:
根据假设(2)可知
因此可知道最大似然概率的计算为:
而接下来要确定最大似然概率,从而去确定假设函数到最终确定分类结果。可以接着前面的梯度上升或者牛顿迭代法来求取。
这就是基本的利用广义线性模型求解的过程。确定y服从的分布,然后确定T、a、b、η,然后得到假设函数的基本模型,然后利用最大似然规律或者其他方法求得最贴近的参数值,从而能够得到最贴近真实的假设函数来解决问题。








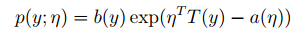
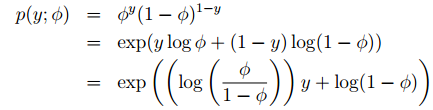
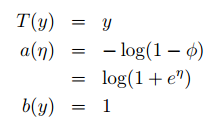
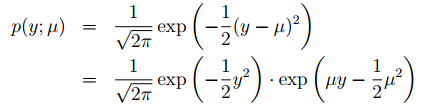

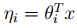
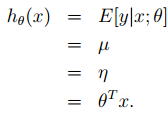
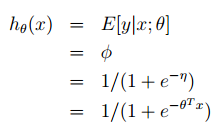
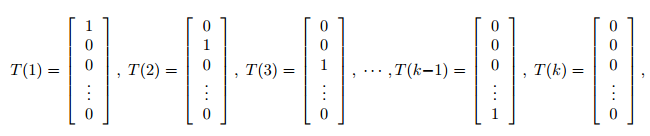
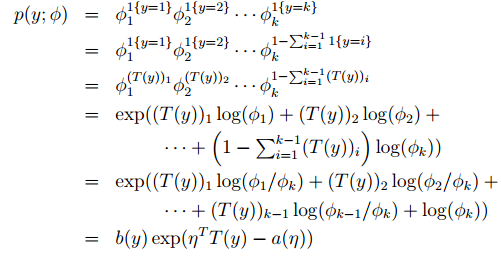
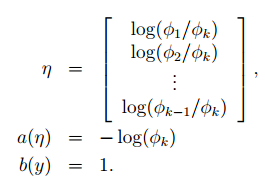
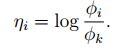
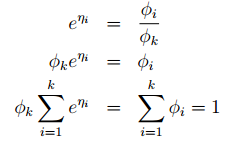
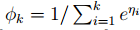
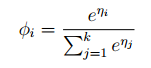
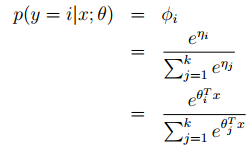
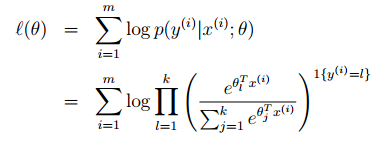















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








