全局空间自相关算法：Join Count

最新推荐文章于 2024-03-23 07:50:42 发布

虾神说D

最新推荐文章于 2024-03-23 07:50:42 发布

阅读量2.9w

点赞数 12

分类专栏： GIS 数据分析文章标签：空间统计算法空间自相关 Join Count MoransI

本文链接：https://blog.csdn.net/allenlu2008/article/details/49895387/

版权

127 篇文章 497 订阅

订阅专栏

124 篇文章 280 订阅

订阅专栏

ArcGIS里面，全局空间自相关只提供了一个Moran's I方法，当然要说一招鲜吃遍天也是可以的，不过关于全局自相关还是有不少其他的方法的，这次给大家介绍一种更加简单并且容易理解的全局空间自相关方法：Join Count方法。

这个方法最早是英国剑桥大学的著名地理学家AndrewD. Cliff 教授和美国乔治敦大学的J. Keith Ord提出，就是下面的两位老帅哥：

后面这个为J. KeithOrd更是厉害，以前说的 General G 指数也有他的一份。

Join Counts这种算法对比那些公式复杂到抓狂的各种算法来说，简单到让人眼前一亮，下面我们来看看他的原理：

首先从他的名字上来看，就能够猜出是怎么完的了。这个算法，就是对两个要素之间的连接类型进行计数，然后根据这个计数来判定聚类还是离散的。

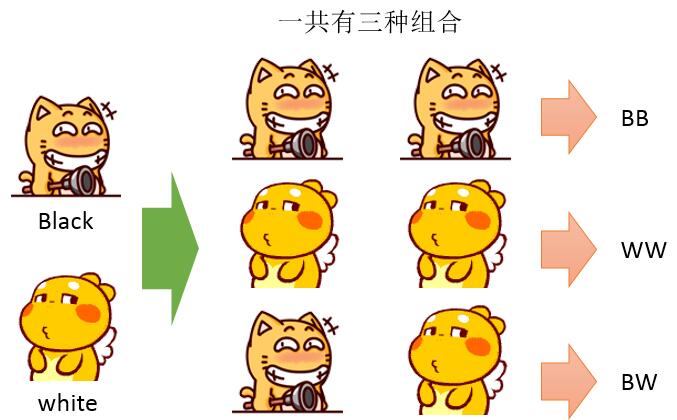
这种类似一种描述二进制之间关系的方式，如黑/白两种颜色，他们之间的关系就有三种：黑-黑（BB）、白-白（WW）、黑-白（BW）。

如下图：

三种情况的概率，就如下所示：（有数学恐惧症的同学请略过）

算出来之后，他们的预期值是：

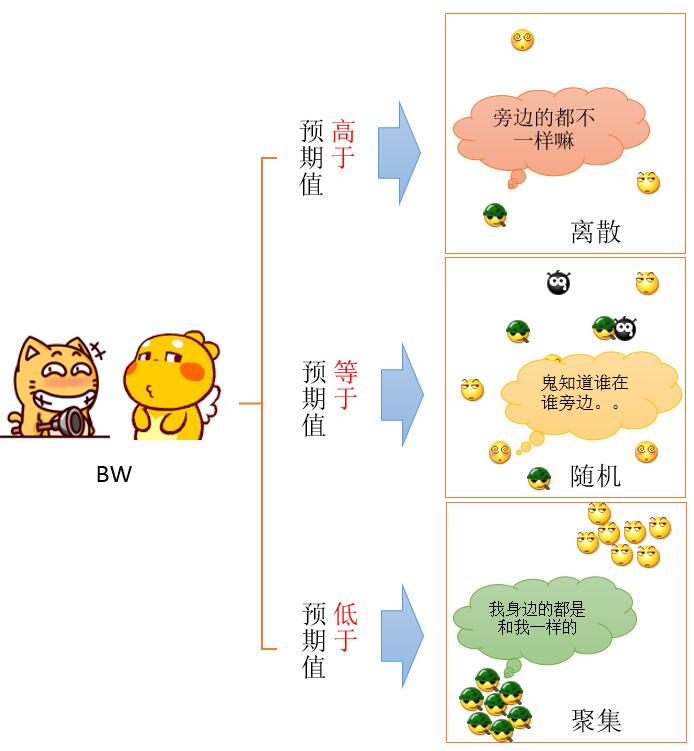
算出三种值来之后，就可以进行比较了，比较的结果如下：

如果BW比我们所期望的数值要低，表示正空间自相关。

如果BW比我们所期望的数值要高，表示负空间自相关。

如果BW比我们所期望的数值均等，表示随机。

如下图所示：

最后，我们来看看分布用我们最属性的Moran's I和join Counts两种方法计算出来的全局空间自相关的结果：

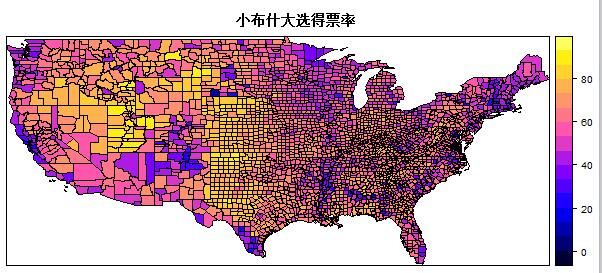
首先是数据，我们选用2004年美国大选中，小布什的得票率来计算，数据如下图：

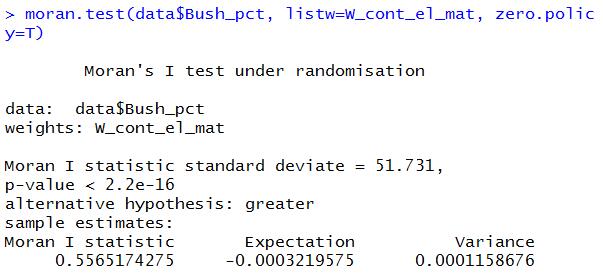
通过Moran's I方法技术出来的结果如下：

下面逐条解答一下上面的各项内容：

数据：data数据集里面的小布什得票数
空间权重（空间关系概念化）：这里是面数据，用的是共点共边就被认为是近邻，用的是“Queen's Case”（这点看不懂的，请去看白话空间统计之五：空间关系概念化（下）里面的描述）
Moran's I统计标准偏差：51.731(统计标准偏差：一种量度数据分布的分散程度之标准，用以衡量数据值偏离算术平均值的程度。标准偏差越小，这些值偏离平均值就越少，反之亦然。标准偏差的大小可通过标准偏差与平均值的倍率关系来衡量。)
p值：2.2e-16，置信度为99%以上，极高置信度区间，说明这份数据效果非常好。
alternative hypothesis（备择假设亦称研究假设，统计学的基本概念之一。假设检验中需要证实的有关总体分布的假设，它包含关于总体分布的一切使原假设不成立的命题。）：极大
Moran's I统计指数：0.5565174275
期望值：-0.0003219575
方差：0.0001158676

因为Moran's I的指数是在-1——1之间，越靠近1的，聚集趋势就越明显，所以根据以上数据，我们可以判定，小布什的得票获胜区域（或者失败区域）有明显的聚集趋势，也就是说，如果他在某个区域获胜，那么在旁边的区域也极有可能获胜，反之亦然。

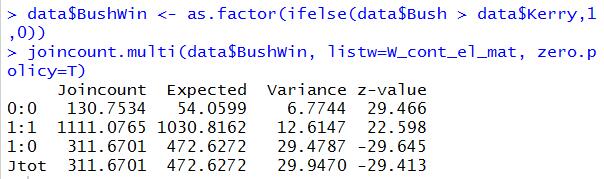
下面是通过Join Count方法进行计算的结果：

因为Join Count只能处理二值化数据，所以第一句就是将值化为二值化，布什获胜的，设置为1，失败的设置为0.

结论解读如下：

从上面的数据可以看出，BB和WW都明显出现了计数值远高于期望值，所以数据呈现聚类模式，其中BB的值方差要小于WW值的方差，所以小布什的获胜选区的聚类程度要略大于失败选区的聚类程度。

而BW的计数小于期望值，可以认为，不存在离散趋势了。

检验统计量表明，BB和WW都是正值，说明我们假设的值比较贴合实际运算结果，是一份比较可信的运算过程。

最后Jtot是所谓的“不同颜色”也就是说，离散偏随机的计数，可以看见与BW的值非常贴近，所以这份数据也表明了随机的可能也是比较低的。

关注