BIRCH算法---使用聚类特征树的多阶段算法

更多数据挖掘代码：https://github.com/linyiqun/DataMiningAlgorithm

介绍

BIRCH算法本身上属于一种聚类算法，不过他克服了一些K-Means算法的缺点，比如说这个k的确定，因为这个算法事先本身就没有设定有多少个聚类。他是通过CF-Tree，(ClusterFeature-Tree)聚类特征树实现的。BIRCH的一个重要考虑是最小化I/O，通过扫描数据库，建立一棵存放于内存的初始CF-树，可以看做多数据的多层压缩。

算法原理

CF聚类特征

说到算法原理，首先就要先知道，什么是聚类特征，何为聚类特征，定义如下：

CF = <n, LS, SS>

聚类特征为一个3维向量，n为数据点总数，LS为n个点的线性和，SS为n个点的平方和。因此又可以得到

x0 = LS/n为簇的中心，以此计算簇与簇之间的距离。

簇内对象的平均距离簇直径，这个可以用阈值T限制，保证簇的一个整体的紧凑程度。簇和簇之间可以进行叠加，其实就是向量的叠加。

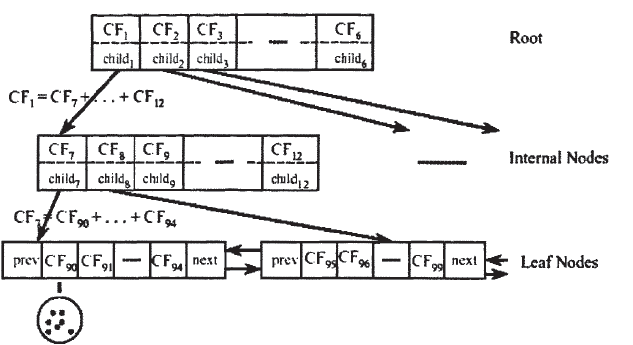
CF-Tree的构造过程

在介绍CF-Tree树，要先介绍3个变量，内部节点平衡因子B，叶节点平衡因子L，簇直径阈值T。B是用来限制非叶子节点的子节点数，L是用来限制叶子节点的子簇个数，T是用来限制簇的紧密程度的，比较的是D--簇内平均对象的距离。下面是主要的构造过程：

1、首先读入第一条数据，构造一个叶子节点和一个子簇，子簇包含在叶子节点中。

2、当读入后面的第2条，第3条，封装为一个簇，加入到一个叶子节点时，如果此时的待加入的簇C的簇直径已经大于T，则需要新建簇作为C的兄弟节点，如果作为兄弟节点，如果此时的叶子节点的孩子节点超过阈值L,则需对叶子节点进行分裂。分裂的规则是选出簇间距离最大的2个孩子，分别作为2个叶子，然后其他的孩子按照就近分配。非叶子节点的分裂规则同上。具体可以对照后面我写的代码。

3、最终的构造模样大致如此：

算法的优点：

1、算法只需扫描一遍就可以得到一个好的聚类效果，而且不需事先设定聚类个数。

2、聚类通过聚类特征树的形式，一定程度上保存了对数据的压缩。

算法的缺点：

1、该算法比较适合球形的簇，如果簇不是球形的，则聚簇的效果将不会很好。

算法的代码实现：