RSA算法从数学基础到实例全面解析

最新推荐文章于 2024-06-20 19:28:59 发布

原创

最新推荐文章于 2024-06-20 19:28:59 发布 · 7.6k 阅读

·

3

·

CC 4.0 BY-SA版权

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

文章标签：

#算法 #解密 #加密 #扩展 #python #function

本文详细介绍了RSA算法的基础，包括同余理论、欧拉函数、费马小定理与欧拉定理，以及扩展欧几里得算法。通过这些数学原理，阐述了密钥生成、加密和解密的过程，并提供了具体的实现步骤。

1、同余（合同式）

转载请注明http://blog.csdn.net/boksic 如有疑问欢迎留言

两个整数 $a$ ， $b$ ，若它们除以正整数 $m$ 所得的余数相等，则称 $a$ ， $b$ 对于模 $m$ 同余

记作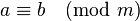 $a \equiv b \pmod{m}$

例如1≡13 (mod 12),可以理解为时钟上1点和13点的指针位置相同

重要性质

$a \equiv b \pmod{m} \Rightarrow \begin{cases} an \equiv bn \pmod{m}, \forall n \in \mathbb{Z} \\ a^n \equiv b^n \pmod{m}, \forall n \in \mathbb{N}^0\end{cases}$

例如1^5=1，13 ^5=371293=30941*12+1

即1^5≡1≡13 ^5(mod 12)

2、欧拉函数（Euler's totient function）

欧拉函数 $φ(n)$ 是少于或等于n的数中与n互质的数的数目，例如 $φ(9) = 6$ ，因为比9小的数中与9互质的有1, 2, 4, 5, 7,8六个数，所以9的欧拉函数为6。

计算方法：

将n分解为质数相乘的形式

$n = p_1^{k_1} \cdots p_r^{k_r}$ ，每个p_i

最低0.47元/天解锁文章

评论 1

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。