引言:Python是最好最热门的编程语言之一,以简单易学、应用广泛、类库强大而著称,是实现机器学习算法的首选语言。本文以人工神经网络的实战为例,证明需要深入理解算法的原理、优劣势等特点以及应用场景,以能达到应用自如的程度。
本文选自《Python大战机器学习:数据科学家的第一个小目标》。
感知机学习算法的原始形式
-
参数
■n:正类的样本点数量,也是负类的样本点数量。总的样本点数量为2n。 -
返回值:所有的样本点组成的数组,形状为(2*n,4)。数组中的每一行代表一个样本点,由其特征x和标记y组成。
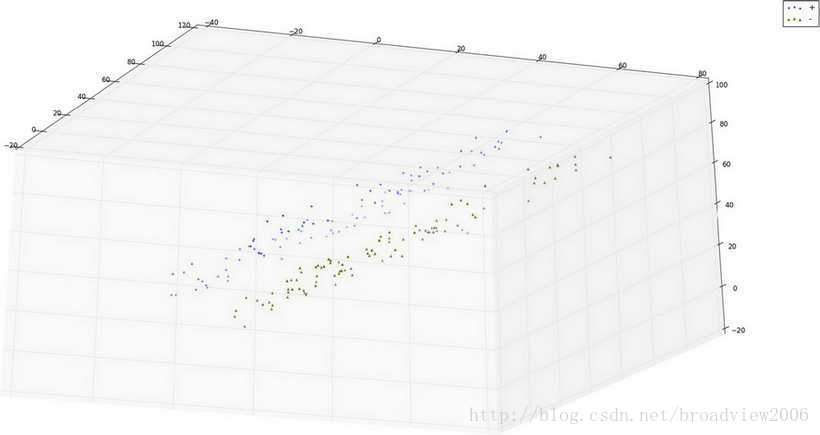
其过程为:首先在z轴坐标为20 的上方生成n个随机点作为正类,在z轴坐标为10 的下方生成n个随机点作为负类。此时在平面z= 10, z= 20 作为隔离带。然后45度旋转x坐标轴,再返回这些点在新坐标轴中的坐标。注意这里混洗了数据,否则会发现数据集的前半部分都是正类,后半部分都是负类,需要混洗数据从而让正负类交叉出现。
- 参数
■ax:一个Axes3D实例,负责绘制图形。
■samples:代表训练数据集的数组,形状为(N,n_features+1),其中N为样本点的个数,n_features代表特征数量(这里为3,表示三个特征)。
然后给出感知机学习算法的原始形式算法的函数(图形如下图所示):
perceptron_data
- 参数
■train_data:代表训练数据集的数组,形状为(N,n_features+1),其中N为样本点的个数,n_features代表特征数量(这里为3,表示三个特征)。
■eta:学习率。
■w_0:即w0,是一个列向量。
■b_0:即b0,是一个标量。
- 返回值:一个元组,成员为w,b 以及迭代次数。
其过程为:
- 最外层循环只有在全部分类正确的这种情况下退出
- 内层循环从前到后遍历所有的样本点。一旦发现某个样本点是误分类点,就更新w,b然后重新从头开始遍历所有的样本点。
由于需要绘制分离超平面,因此需要根据w,b 给出生成分离超平面的函数:
- 参数
■x:分离超平面上点的x坐标组成的数组。
■y:分离超平面上点的y坐标组成的数组。
■w:即w,超平面的法向量,它是一个列向量。
■b:即b,超平面的截距。
- 返回值:分离超平面上点的z坐标组成的数组。
其过程就是根据wxx+wyy+wzz+b=0这个方程求得的。
算法得到的w为[[-10.1] [-68.08433252][ 64.85174234]],分离超平面法向量为(-10.1,-68.08,64.85),它在y-z平面上的投影是一条直线,该直线的斜率为68.08/64.85=1.05,非常接近我们在生成数据时旋转45度角的设定。感知机学习算法的原始形式算法的函数perceptron_original 图形(如下图所示)。
本文选自《Python大战机器学习:数据科学家的第一个小目标》,点此链接可在博文视点官网查看此书。
想及时获得更多精彩文章,可在微信中搜索“博文视点”或者扫描下方二维码并关注。












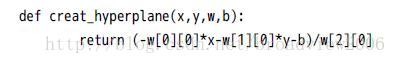



















 4647
4647

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








