机器学习降维方法

特征降维方法包括：Lasso，PCA，小波分析，LDA，奇异值分解SVD，拉普拉斯特征映射，SparseAutoEncoder，局部线性嵌入LLE，等距映射Isomap，Embedding。

1. LASSO通过参数缩减达到降维的目的。

LASSO(Least absolute shrinkage and selection operator, Tibshirani(1996)) 
该方法是一种压缩估计，通过构造一个罚函数得到一个较为精炼的模型，使得压缩一些系数，同时设定一些系数为零。英雌保留了子集收缩的优点，，是一种处理具有复共线性数据的有偏估计。Lasso 的基本思想是在回归系数的绝对值之和小于一个常数的约束条件下，使残差平方和最小化，从而能够产生某些严格等于 0 的回归系数，得到可以解释的模型。

2. 主成分分析PCA

PCA（Principal Component Analysis）是一种常用的数据分析方法。PCA通过线性变换将原始数据变换为一组各维度线性无关的表示，可用于提取数据的主要特征分量，常用于高维数据的降维。 
设有m条n维数据。

1）将原始数据按列组成n行m列矩阵X 
2）将X的每一行（代表一个属性字段）进行零均值化，即减去这一行的均值 
3）求出协方差矩阵C=\frac{1}{m}XX^\mathsf{T} 
4）求出协方差矩阵的特征值及对应的特征向量 
5）将特征向量按对应特征值大小从上到下按行排列成矩阵，取前k行组成矩阵P 
6）Y=PX即为降维到k维后的数据

PCA降维过程请参考http://www.cnblogs.com/zhangchaoyang/articles/2222048.html

3. 小波分析

小波分析有一些变换的操作降低其他干扰可以看做是降维。 
http://www.360doc.com/content/15/0613/14/21899328_477836495.shtml

4. 线性判别LDA

线性判别式分析（Linear Discriminant Analysis），简称为LDA。也称为Fisher线性判别（Fisher Linear Discriminant，FLD），是模式识别的经典算法，在1996年由Belhumeur引入模式识别和人工智能领域。

基本思想是将高维的模式样本投影到最佳鉴别矢量空间，以达到抽取分类信息和压缩特征空间维数的效果，投影后保证模式样本在新的子空间有最大的类间距离和最小的类内距离，即模式在该空间中有最佳的可分离性。

LDA与前面介绍过的PCA都是常用的降维技术。PCA主要是从特征的协方差角度，去找到比较好的投影方式。LDA更多的是考虑了标注，即希望投影后不同类别之间数据点的距离更大，同一类别的数据点更紧凑。

详细请参考http://www.cnblogs.com/zhangchaoyang/articles/2644095.html

5. 拉普拉斯映射

拉普拉斯特征映射将处于流形上的数据，在尽量保留原数据间相似度的情况下，映射到低维下表示。

求解广义特征向量，取前几个非零最小特值对应的特向，即为原数据在低维下的表示。 
资料来源于：http://blog.csdn.net/yujianmin1990/article/details/48420483

6. 深度学习SparseAutoEncoder

稀疏自编码就是用少于输入层神经元数量的隐含层神经元去学习表征输入层的特征，相当于把输入层的特征压缩了，所以是特征降维。 
详细请参考http://blog.csdn.net/whiteinblue/article/details/20639629

7. 矩阵奇异值分解SVD

在PCA算法中，用到了SVD，类似PCA，可以看成一类。

8. LLE局部线性嵌入

Locally linear embedding（LLE）是一种非线性降维算法，它能够使降维后的数据较好地保持原有流形结构。LLE可以说是流形学习方法最经典的工作之一。很多后续的流形学习、降维方法都与LLE有密切联系。

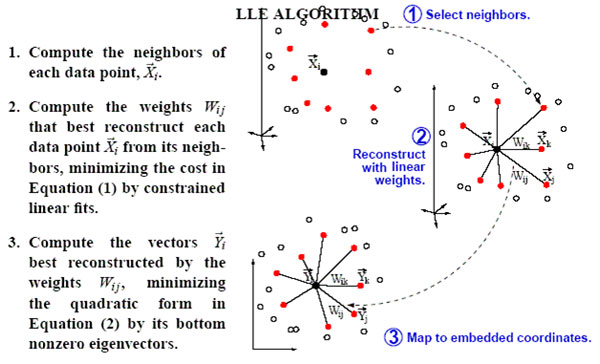
LLE算法认为每一个数据点都可以由其近邻点的线性加权组合构造得到。算法的主要步骤分为三步：(1)寻找每个样本点的k个近邻点；（2）由每个样本点的近邻点计算出该样本点的局部重建权值矩阵；（3）由该样本点的局部重建权值矩阵和其近邻点计算出该样本点的输出值。具体的算法流程如图2所示：

 

9. Isomap等距映射

Isomap是一种非迭代的全局优化算法，通过一种原本试用于欧式空间的算法MDS，达到降维的目的。

参考资料：

10.Embedding

word2vec, fm, nn

http://www.36dsj.com/archives/26723