| Time Limit: 3000MS | Memory Limit: 30000K | |
| Total Submissions: 2457 | Accepted: 1020 |
Description
One day a snail climbed up to a big tree and finally came to the end of a branch. What a different feeling to look down from such a high place he had never been to before! However, he was very tired due to the long time of climbing, and fell asleep. An unbelievable thing happened when he woke up ---- he found himself lying in a meadow and his house originally on his back disappeared! Immediately he realized that he fell off the branch when he was sleeping! He was sure that his house must still be on the branch he had been sleeping on. The snail began to climb the tree again, since he could not live without his house.
When reaching the first fork of the tree, he sadly found that he could not remember the route that he climbed before. In order to find his lovely house, the snail decided to go to the end of every branch. It was dangerous to walk without the protection of the house, so he wished to search the tree in the best way.
Fortunately, there lived many warm-hearted worms in the tree that could accurately tell the snail whether he had ever passed their places or not before he fell off.
Now our job is to help the snail. We pay most of our attention to two parts of the tree ---- the forks of the branches and the ends of the branches, which we call them key points because key events always happen there, such as choosing a path, getting the help from a worm and arriving at the house he is searching for.
Assume all worms live at key points, and all the branches between two neighboring key points have the same distance of 1. The snail is now at the first fork of the tree.
Our purpose is to find a proper route along which he can find his house as soon as possible, through the analysis of the structure of the tree and the locations of the worms. The only restriction on the route is that he must not go down from a fork until he has reached all the ends grown from this fork.
The house may be left at the end of any branches in an equal probability. We focus on the mathematical expectation of the distance the snail has to cover before arriving his house. We wish the value to be as small as possible.
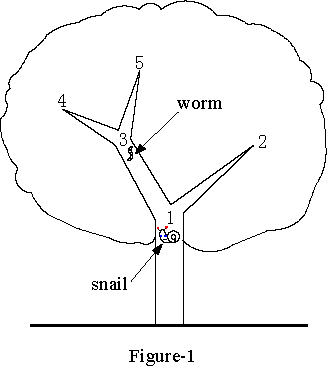
As illustrated in Figure-1, the snail is at the key point 1 and his house is at a certain point among 2, 4 and 5. A worm lives at point 3, who can tell the snail whether his house is at one of point 4 and 5 or not. Therefore, the snail can choose two strategies. He can go to point 2 first. If he cannot find the house there, he should go back to point 1, and then reaches point 4 (or 5) by point 3. If still not, he has to return point 3, then go to point 5 (or 4), where he will undoubtedly find his house. In this choice, the snail covers distances of 1, 4, 6 corresponding to the circumstances under which the house is located at point 2, 4 (or 5), 5 (or 4) respectively. So the expectation value is (1 + 4 + 6) / 3 = 11 / 3. Obviously, this strategy does not make full use of the information from the worm. If the snail goes to point 3 and gets useful information from the worm first, and then chooses to go back to point 1 then towards point 2, or go to point 4 or 5 to take his chance, the distances he covers will be 2, 3, 4 corresponding to the different locations of the house. In such a strategy, the mathematical expectation will be (2 + 3 + 4) / 3 = 3, and it is the very route along which the snail should search the tree.
When reaching the first fork of the tree, he sadly found that he could not remember the route that he climbed before. In order to find his lovely house, the snail decided to go to the end of every branch. It was dangerous to walk without the protection of the house, so he wished to search the tree in the best way.
Fortunately, there lived many warm-hearted worms in the tree that could accurately tell the snail whether he had ever passed their places or not before he fell off.
Now our job is to help the snail. We pay most of our attention to two parts of the tree ---- the forks of the branches and the ends of the branches, which we call them key points because key events always happen there, such as choosing a path, getting the help from a worm and arriving at the house he is searching for.
Assume all worms live at key points, and all the branches between two neighboring key points have the same distance of 1. The snail is now at the first fork of the tree.
Our purpose is to find a proper route along which he can find his house as soon as possible, through the analysis of the structure of the tree and the locations of the worms. The only restriction on the route is that he must not go down from a fork until he has reached all the ends grown from this fork.
The house may be left at the end of any branches in an equal probability. We focus on the mathematical expectation of the distance the snail has to cover before arriving his house. We wish the value to be as small as possible.
As illustrated in Figure-1, the snail is at the key point 1 and his house is at a certain point among 2, 4 and 5. A worm lives at point 3, who can tell the snail whether his house is at one of point 4 and 5 or not. Therefore, the snail can choose two strategies. He can go to point 2 first. If he cannot find the house there, he should go back to point 1, and then reaches point 4 (or 5) by point 3. If still not, he has to return point 3, then go to point 5 (or 4), where he will undoubtedly find his house. In this choice, the snail covers distances of 1, 4, 6 corresponding to the circumstances under which the house is located at point 2, 4 (or 5), 5 (or 4) respectively. So the expectation value is (1 + 4 + 6) / 3 = 11 / 3. Obviously, this strategy does not make full use of the information from the worm. If the snail goes to point 3 and gets useful information from the worm first, and then chooses to go back to point 1 then towards point 2, or go to point 4 or 5 to take his chance, the distances he covers will be 2, 3, 4 corresponding to the different locations of the house. In such a strategy, the mathematical expectation will be (2 + 3 + 4) / 3 = 3, and it is the very route along which the snail should search the tree.

Input
The input contains several sets of test data. Each set begins with a line containing one integer N, no more than 1000, which indicates the number of key points in the tree. Then follow N lines describing the N key points. For convenience, we number all the key points from 1 to N. The key point numbered with 1 is always the first fork of the tree. Other numbers may be any key points in the tree except the first fork. The i-th line in these N lines describes the key point with number i. Each line consists of one integer and one uppercase character 'Y' or 'N' separated by a single space, which represents the number of the previous key point and whether there lives a worm ('Y' means lives and 'N' means not). The previous key point means the neighboring key point in the shortest path between this key point and the key point numbered 1. In the above illustration, the previous key point of point 2 or 3 is point 1, while the previous key point of point 4 or 5 is point 3. This integer is -1 for the key point 1, means it has no previous key point. You can assume a fork has at most eight branches. The first set in the sample input describes the above illustration.
A test case of N = 0 indicates the end of input, and should not be processed.
A test case of N = 0 indicates the end of input, and should not be processed.
Output
Output one line for each set of input data. The line contains one float number with exactly four digits after the decimal point, which is the mathematical expectation value.
Sample Input
5 -1 N 1 N 1 Y 3 N 3 N 10 -1 N 1 Y 1 N 2 N 2 N 2 N 3 N 3 Y 8 N 8 N 6 -1 N 1 N 1 Y 1 N 3 N 3 N 0
Sample Output
3.0000 5.0000 3.5000
Source
Beijing 2004
题目大意:一只蜗牛起初幸福地谁在一个树叶子上,后来由于种种原因掉到树根了,可是壳还在上面,现在想要回到原始的叶子,问需要走的步数的最小期望值。
一直树上某些点有毛毛虫,当蜗牛爬到这里时,他们会告诉蜗牛掉落时经没经过这里,这样就可以节省一大部分可能的路程。
固定1为根,先输入节点数n,之后n行每行一个u char表示父亲编号(-1表示无父亲——根节点)和当前节点是否有毛毛虫(Y/N)
求最小期望,其实就是求最小的合计路程/路径数。路径数是固定的,也就是叶子数。
这样通过dp可以想办法求出对于每个节点为起点时,往下走的总路径长度。方法如下:
对于某个节点u 后面会有很多个孩子节点v0,v1,v2...
对于有虫子的节点,对于最终的贡献就是该节点往后的所有路程,并且对于后续不会有额外贡献。
对于没虫子的节点,遍历完它和它的分支后,如果还要遍历其余点,那么每多遍历一个叶子,都要再遍历一次这个节点后的所有叶子。也就是对于后续节点的遍历会有一个持续的贡献。而这个贡献其实就是从这个孩子节点往后的最长路线,也就是遍历完所有叶子后返回该节点的路径长度,这样有需要dp一个新值。
其次,每当多一个孩子时,需要累加2,也就是从父亲到孩子再返回父亲。同时,这个值需要累加到后续的遍历中。
不太怎么好想,反正我是WA了半天……是因为对于后续的贡献直接用子树的总贡献,但这样会导致累加许多路程,其实对于每个子树,对于后续的贡献只是遍历所有叶子的总路程,这个。。说的有点乱=。=
对于u的多个孩子的遍历顺序,我是搜的,。。很慢……
代码如下:
之后是一个排序版,一开始对于排序我也感觉很谜,。不太相信它的正确性。后来仔细想想确实很科学~
因为对于两个节点的先后顺序,其实与其余的点无关,因为不管这两个点的位置怎么样,其余点的最终贡献不会变。
而这两个点的相对位置,是看谁在前可以让多余的路程更少,也就是代码中的cmp函数来替代搜索~
题目大意:一只蜗牛起初幸福地谁在一个树叶子上,后来由于种种原因掉到树根了,可是壳还在上面,现在想要回到原始的叶子,问需要走的步数的最小期望值。
一直树上某些点有毛毛虫,当蜗牛爬到这里时,他们会告诉蜗牛掉落时经没经过这里,这样就可以节省一大部分可能的路程。
固定1为根,先输入节点数n,之后n行每行一个u char表示父亲编号(-1表示无父亲——根节点)和当前节点是否有毛毛虫(Y/N)
求最小期望,其实就是求最小的合计路程/路径数。路径数是固定的,也就是叶子数。
这样通过dp可以想办法求出对于每个节点为起点时,往下走的总路径长度。方法如下:
对于某个节点u 后面会有很多个孩子节点v0,v1,v2...
对于有虫子的节点,对于最终的贡献就是该节点往后的所有路程,并且对于后续不会有额外贡献。
对于没虫子的节点,遍历完它和它的分支后,如果还要遍历其余点,那么每多遍历一个叶子,都要再遍历一次这个节点后的所有叶子。也就是对于后续节点的遍历会有一个持续的贡献。而这个贡献其实就是从这个孩子节点往后的最长路线,也就是遍历完所有叶子后返回该节点的路径长度,这样有需要dp一个新值。
其次,每当多一个孩子时,需要累加2,也就是从父亲到孩子再返回父亲。同时,这个值需要累加到后续的遍历中。
不太怎么好想,反正我是WA了半天……是因为对于后续的贡献直接用子树的总贡献,但这样会导致累加许多路程,其实对于每个子树,对于后续的贡献只是遍历所有叶子的总路程,这个。。说的有点乱=。=
对于u的多个孩子的遍历顺序,我是搜的,。。很慢……
代码如下:
#include <iostream>
#include <cmath>
#include <vector>
#include <cstdlib>
#include <cstdio>
#include <cstring>
#include <queue>
#include <stack>
#include <list>
#include <algorithm>
#include <map>
#include <set>
#define LL long long
#define Pr pair<int,int>
#define fread() freopen("in.in","r",stdin)
#define fwrite() freopen("out.out","w",stdout)
using namespace std;
const int INF = 0x3f3f3f3f;
const int msz = 10000;
const int mod = 1e9+7;
const double eps = 1e-8;
struct Edge
{
int v,next;
};
int head[2333];
Edge eg[2333];
bool worm[2333];
bool vis[8];
//0存路径数 1存路程 2存最远路径
int dp[2333][3];
int ans;
int find(int *id,int ad,int hs,int tp)
{
if(hs == tp) return 0;
int mn = INF;
for(int i = 0; i < tp; ++i)
{
if(vis[i]) continue;
vis[i] = 1;
mn = min(mn,dp[id[i]][1]+ad*dp[id[i]][0]+find(id,ad+2+(worm[id[i]]? 0: dp[id[i]][2]),hs+1,tp));
vis[i] = 0;
}
return mn;
}
void dfs(int u)
{
dp[u][0] = dp[u][1] = dp[u][2] = 0;
if(head[u] == -1)
{
dp[u][0]++;
return;
}
int v;
int id[8];
int tp = 0;
for(int i = head[u]; i != -1; i = eg[i].next)
{
v = eg[i].v;
dfs(v);
id[tp++] = v;
dp[u][0] += dp[v][0];
if(!worm[v]) dp[u][2] += dp[v][2];
}
memset(vis,0,sizeof(vis));
dp[u][2] += tp*2;
dp[u][1] = find(id,1,0,tp);
//printf("%d:路径:%d 路程:%d worm:%c\n",u,dp[u][0],dp[u][1],worm[u]? 'Y': 'N');
//for(int i = 0; i < tp; ++i)
//printf("%d:路径:%d 路程:%d worm:%c\n",id[i],dp[id[i]][0],dp[id[i]][1],worm[id[i]]? 'Y': 'N');
}
int main()
{
//fread();
//fwrite();
int n,u;
char ch[2];
while(~scanf("%d",&n) && n)
{
memset(head,-1,sizeof(head));
for(int i = 1; i <= n; ++i)
{
scanf("%d%s",&u,ch);
if(i != 1)
{
eg[i].v = i;
eg[i].next = head[u];
head[u] = i;
worm[i] = (ch[0] == 'Y');
}
}
dfs(1);
printf("%.4f\n",dp[1][1]*1.0/dp[1][0]);
}
return 0;
}
之后是一个排序版,一开始对于排序我也感觉很谜,。不太相信它的正确性。后来仔细想想确实很科学~
因为对于两个节点的先后顺序,其实与其余的点无关,因为不管这两个点的位置怎么样,其余点的最终贡献不会变。
而这两个点的相对位置,是看谁在前可以让多余的路程更少,也就是代码中的cmp函数来替代搜索~
#include <iostream>
#include <cmath>
#include <vector>
#include <cstdlib>
#include <cstdio>
#include <cstring>
#include <queue>
#include <stack>
#include <list>
#include <algorithm>
#include <map>
#include <set>
#define LL long long
#define Pr pair<int,int>
#define fread() freopen("in.in","r",stdin)
#define fwrite() freopen("out.out","w",stdout)
using namespace std;
const int INF = 0x3f3f3f3f;
const int msz = 10000;
const int mod = 1e9+7;
const double eps = 1e-8;
struct Edge
{
int v,next;
};
int head[2333];
Edge eg[2333];
bool worm[2333];
bool vis[8];
//0存路径数 1存路程 2存最远路径
int dp[2333][3];
int ans;
bool cmp(int a,int b)
{
return dp[b][2]*dp[a][0] > dp[a][2]*dp[b][0];
}
void dfs(int u)
{
dp[u][0] = dp[u][1] = dp[u][2] = 0;
if(head[u] == -1)
{
dp[u][0]++;
return;
}
int v;
int id[8];
int tp = 0;
for(int i = head[u]; i != -1; i = eg[i].next)
{
v = eg[i].v;
dfs(v);
id[tp++] = v;
dp[u][0] += dp[v][0];
if(worm[v])
{
dp[v][2] = 0;
}
dp[v][2] += 2;
dp[u][2] += dp[v][2];
}
int tmp = 1;
sort(id,id+tp,cmp);
for(int i = 0; i < tp; ++i)
{
dp[u][1] += dp[id[i]][1]+tmp*dp[id[i]][0];
tmp += dp[id[i]][2];
}
//printf("%d:路径:%d 路程:%d worm:%c\n",u,dp[u][0],dp[u][1],worm[u]? 'Y': 'N');
//for(int i = 0; i < tp; ++i)
//printf("%d:路径:%d 路程:%d worm:%c\n",id[i],dp[id[i]][0],dp[id[i]][1],worm[id[i]]? 'Y': 'N');
}
int main()
{
//fread();
//fwrite();
int n,u;
char ch[2];
while(~scanf("%d",&n) && n)
{
memset(head,-1,sizeof(head));
for(int i = 1; i <= n; ++i)
{
scanf("%d%s",&u,ch);
if(i != 1)
{
eg[i].v = i;
eg[i].next = head[u];
head[u] = i;
worm[i] = (ch[0] == 'Y');
}
}
dfs(1);
printf("%.4f\n",dp[1][1]*1.0/dp[1][0]);
}
return 0;
}

























 99
99











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








