hdu4565 So Easy!(矩阵快速幂)

题意：

告诉你a,b,n,m,求

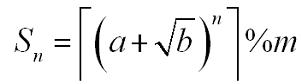
0<a,m<2^15 , (a-1)^2<b<a^2 , 0<b,n<2^31

解题思路：

    我们首先对（a+sqrt(b))^n进行处理， 由 a+sqrt(b))^n的展开式我们可以知道

(a+sqrt(b))^n = Xn + Yn * sqrt(b);

那么

( a + sqrt( b ) )^( n + 1 ) = ( a + sqrt( b ) ) * ( Xn + Yn * sqrt(b) ) = ( a * Xn + b * Yn ) + ( a * Yn + Xn ) * sqrt( b );

则

Xn +1 = ( a * Xn + b * Yn )

Yn +1 = ( a * Yn + Xn )

将其转化为矩阵，则

递推下去可以得到

所以

Xn = a * X 0 + b * Y 0;

Yn = X 0 + a * Y 0;

由于 (a-1)^2<b<a^2 ，

那么 0 < ( a - sqrt( b ) )^ n < 1

 又   ( a + sqrt( b ) )^ n + ( a - sqrt( b ) )^ n = 2 * Xn

那么 ( a + sqrt( b ) )^ n 向上取整的值就是 2 * Xn

最终

    Sn = （ 2 * Xn ）% m;

参考代码：

#include <iostream>
#include <math.h>
#include <stdio.h>
using namespace std;
typedef long long ll;
struct Matrix{
	ll mat[2][2];
};
Matrix mul(Matrix a,Matrix b,ll mod){
	Matrix ans;
	for (int i=0;i<2;i++){
		for (int j=0;j<2;j++){
			ans.mat[i][j]=0;
			for (int k=0;k<2;k++){
				ans.mat[i][j]=(ans.mat[i][j]+a.mat[i][k]*b.mat[k][j]);
				ans.mat[i][j]%=mod;
			}
		}
	}
	return ans;
}
Matrix Init(){
	Matrix ans;
	for (int i=0;i<2;i++){
		for (int j=0;j<2;j++){
			if (i==j)
				ans.mat[i][j]=1;
			else
				ans.mat[i][j]=0;
		}
	}
	return ans;
}
Matrix exp(Matrix a,ll k,ll m){
	Matrix ans=Init();
	while (k){
		if (k&1)
			ans=mul(ans,a,m);
		a=mul(a,a,m);
		k>>=1;
	}
	return ans;
}
int main(){
	Matrix M;
	ll a,b,n;
	ll m;
	while (~scanf("%lld%lld%lld%lld",&a,&b,&n,&m)){
		M.mat[0][0]=M.mat[1][1]=a;
		M.mat[0][1]=b;
		M.mat[1][0]=1;
		Matrix ans=exp(M,n,m);
		/*
		for (int i=0;i<2;i++){
			for (int j=0;j<2;j++)
				cout<<ans.mat[i][j]<<" ";
			cout<<endl;
		}
		*/
		ll x=ans.mat[0][0];

		cout<<(2*x)%m<<endl;
	}
	return 0;
}