ChrisRenke/DrawerArrowDrawable源码解析

最新推荐文章于 2024-05-16 10:08:06 发布

crazy__chen

最新推荐文章于 2024-05-16 10:08:06 发布

阅读量3.2k

点赞数 3

分类专栏：源码解析 android开发 Android控件源码解析

本文链接：https://blog.csdn.net/crazy__chen/article/details/46334843

版权

android开发同时被 3 个专栏收录

86 篇文章 2 订阅

订阅专栏

源码解析

23 篇文章 0 订阅

订阅专栏

Android控件源码解析

13 篇文章 8 订阅

订阅专栏

转载请注明出处http://blog.csdn.net/crazy__chen/article/details/46334843

源码下载地址http://download.csdn.net/detail/kangaroo835127729/8765757

这次解析的控件DrawerArrowDrawable是一款侧拉抽屉效果的控件，在很多应用上我们都可以看到(例如知乎)，控件的github地址为https://github.com/ChrisRenke/DrawerArrowDrawable

大家可以先来看一下控件的效果

这个控件的作者，也写过一篇文章对控件的制作过程做了说明，其中更多的是涉及箭头的变换具体算法，我在本文中将简化对算法的说明(因为比较复杂，我会提供给大家算法的思路)。如果大家对原文感兴趣，可以参考这个地址http://chrisrenke.com/drawerarrowdrawable/

另外还有一篇中文翻译http://www.eoeandroid.com/thread-561707-1-1.html?_dsign=e25beff0

下面我来说一下这个控件的具体制作方法。

首先我们可以看到，有一个侧拉抽屉的效果，这个效果是用android.support.v4包提供的android.support.v4.widget.DrawerLayout来实现的，对于这个控件，大家导入对应包，就可以使用。例如

<!-- Content -->
  <android.support.v4.widget.DrawerLayout
      android:id="@+id/drawer_layout"
      android:layout_width="match_parent"
      android:layout_height="0dp"
      android:layout_weight="1"
      >

    <TextView
        android:id="@+id/view_content"
        android:layout_width="match_parent"
        android:layout_height="match_parent"
        android:gravity="center"
        android:textColor="#000000"
        android:text="@string/content_hint"
        android:background="#ffffff"
        />

    <TextView
        android:id="@+id/drawer_content"
        android:layout_width="240dp"
        android:layout_height="match_parent"
        android:layout_gravity="start"
        android:gravity="center"
        android:text="@string/drawer_hint"
        android:textColor="@color/light_gray"
        android:background="@color/darker_gray"
        />

  </android.support.v4.widget.DrawerLayout>

上面的xml，其实就是定义了一个侧拉抽屉，其中在.DrawerLayout中的第一个控件，会被当成是抽屉，而第二个控件，会被当成主要内容。

由此可见，侧拉的效果是很容易实现(使用google提供的包)。

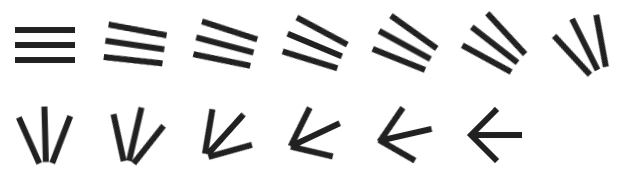
然而对比我们的DrawerArrowDrawable，会发现DrawerArrowDrawable有一个非常炫的效果，就是标题栏上的箭头变化。在初始状态，箭头是三条横线，当侧拉时，三条横线逐渐聚合成箭头，当侧拉返回时，又由箭头分散为三条横线。

本质上，这个箭头的实现，就是整个DrawerArrowDrawable的难点，大家可能一下子没有太好的思路。

我们先来看一下箭头变化的过程图

对于整个箭头整体，本质上是一个drawable,也就是说我们自定义一个drawable(这种方法我们在本专栏的其他文章也见过)，修改它的ondraw方法，来实现一些复制的动画效果。

对于DrawerArrowDrawable，我们先关注三条横线中的第一条，对于第一条横线，有首尾两个点(这个两个点决定了这条横线)。下面的说明都是针对第一条横线而言(其他横线的原理和第一条是一样的)

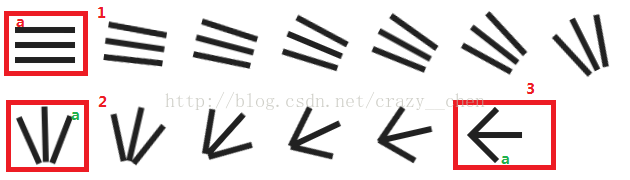
横线在初始状态，有首尾两个点，称为a,b。a，b在整个箭头变化过程中，所在位置不断变化，从而构成一条轨迹(a,b各自一条)

我们将这个箭头状态分成三部分，如下

对于1,2,3三个状态，我们只考察a点，对于a点而言，状态1，到状态2，可以形成一个轨迹，是一个贝塞尔曲线(什么是贝塞尔曲线，大家可以自行百度，简而言之就是由一系列控制点（至少一个），可以确定两点之间的一条平滑曲线)。

有人会问，凭什么确定这是一条贝塞尔曲线呢，其实我们没有办法确定，但是我们可以确定一条贝塞尔曲线，使之近似等于a点的运动过轨，也就是说我们是把a点的轨迹抽象成函数，然后通过这个函数，我们就可以确定轨迹上每一点的坐标了。注意，这里的因果关系要弄明白，是现有轨迹，后有曲线，这个控件的作者，也是根据实际的轨迹，推算出轨迹的函数表达式的。

Ok,那么我们也容易知道，状态2到状态3，a点的轨迹，是另外一条贝塞尔曲线

同理，b点整个过程的轨迹，也就是两条贝塞尔曲线，而两点确定一条直线，根据a,b两个的轨迹，我们就能确定横线的轨迹了。

其他横线同理。所以要实现箭头的变换效果，我们只要根据贝塞尔曲线，不断绘制这个三天横线就可以了。

那么，对应到具体的java代码，我们应该怎么实现呢？下面开始结合源码进行说明。

首先来看构造函数和初始化

public DrawerArrowDrawable(Resources resources, boolean rounded) {
	    this.rounded = rounded;
	    float density = resources.getDisplayMetrics().density;
	    float strokeWidthPixel = STROKE_WIDTH_DP * density;
	    halfStrokeWidthPixel = strokeWidthPixel / 2;
	
	    linePaint = new Paint(Paint.SUBPIXEL_TEXT_FLAG | Paint.ANTI_ALIAS_FLAG);
	    /* 当画笔样式为STROKE或FILL_OR_STROKE时，设置笔刷的图形样式，如圆形样式
	     * Cap.ROUND,或方形样式Cap.SQUARE
	     */	   
	    linePaint.setStrokeCap(rounded ? Cap.ROUND : Cap.BUTT);
	    //画笔颜色
	    linePaint.setColor(Color.BLACK);
	    //设置画笔的样式，为FILL，FILL_OR_STROKE，或STROKE，也就是画轮廓，而fill是填充  
	    linePaint.setStyle(Paint.Style.STROKE);
	    //设置空心的边框宽度
	    linePaint.setStrokeWidth(strokeWidthPixel);
	
	    int dimen = (int) (DIMEN_DP * density);
	    bounds = new Rect(0, 0, dimen, dimen);
	
	    Path first, second;
	    JoinedPath joinedA, joinedB;
	
	    // Top 第一条横线
	    first = new Path();
	    first.moveTo(5.042f, 20f);
	    //实现贝塞尔曲线,(x1,y1) 为控制点，(x2,y2)为控制点，(x3,y3) 为结束点
	    first.rCubicTo(8.125f, -16.317f, 39.753f, -27.851f, 55.49f, -2.765f);
	    second = new Path();
	    second.moveTo(60.531f, 17.235f);
	    second.rCubicTo(11.301f, 18.015f, -3.699f, 46.083f, -23.725f, 43.456f);	    
	    scalePath(first, density);
	    scalePath(second, density);
	    joinedA = new JoinedPath(first, second);
	
	    first = new Path();
	    first.moveTo(64.959f, 20f);
	    first.rCubicTo(4.457f, 16.75f, 1.512f, 37.982f, -22.557f, 42.699f);
	    second = new Path();
	    second.moveTo(42.402f, 62.699f);
	    second.cubicTo(18.333f, 67.418f, 8.807f, 45.646f, 8.807f, 32.823f);
	    scalePath(first, density);
	    scalePath(second, density);
	    joinedB = new JoinedPath(first, second);
	    topLine = new BridgingLine(joinedA, joinedB);
	
	    // Middle 第二条
	    first = new Path();
	    first.moveTo(5.042f, 35f);	    
	    first.cubicTo(5.042f, 20.333f, 18.625f, 6.791f, 35f, 6.791f);
	    second = new Path();
	    second.moveTo(35f, 6.791f);
	    second.rCubicTo(16.083f, 0f, 26.853f, 16.702f, 26.853f, 28.209f);
	    scalePath(first, density);
	    scalePath(second, density);
	    joinedA = new JoinedPath(first, second);
	
	    first = new Path();
	    first.moveTo(64.959f, 35f);
	    first.rCubicTo(0f, 10.926f, -8.709f, 26.416f, -29.958f, 26.416f);
	    second = new Path();
	    second.moveTo(35f, 61.416f);
	    second.rCubicTo(-7.5f, 0f, -23.946f, -8.211f, -23.946f, -26.416f);
	    scalePath(first, density);
	    scalePath(second, density);
	    joinedB = new JoinedPath(first, second);
	    middleLine = new BridgingLine(joinedA, joinedB);
	
	    // Bottom 第三条
	    first = new Path();
	    first.moveTo(5.042f, 50f);
	    first.cubicTo(2.5f, 43.312f, 0.013f, 26.546f, 9.475f, 17.346f);
	    second = new Path();
	    second.moveTo(9.475f, 17.346f);
	    second.rCubicTo(9.462f, -9.2f, 24.188f, -10.353f, 27.326f, -8.245f);
	    scalePath(first, density);
	    scalePath(second, density);
	    joinedA = new JoinedPath(first, second);
	
	    first = new Path();
	    first.moveTo(64.959f, 50f);
	    first.rCubicTo(-7.021f, 10.08f, -20.584f, 19.699f, -37.361f, 12.74f);
	    second = new Path();
	    second.moveTo(27.598f, 62.699f);
	    second.rCubicTo(-15.723f, -6.521f, -18.8f, -23.543f, -18.8f, -25.642f);
	    scalePath(first, density);
	    scalePath(second, density);
	    joinedB = new JoinedPath(first, second);
	    bottomLine = new BridgingLine(joinedA, joinedB);
	  }

上面的代码有点多，先看开始部分，发现是一些初始化属性的代码，做了画笔初始化的工作，使用bounds保存了drawable的大小信息。

注意到，还计算了当前屏幕的密度，这个密度非常重要。为什么呢？

根据上面的说法，作者是根据轨迹，计算出曲线的，但是这个曲线的具体方程，跟作者用来计算的屏幕大小是有关的。例如作者屏幕上，状态2，a点的坐标是(10,10)，那么在你的屏幕上，假设你的屏幕密度是作者的两倍，那么a的坐标，可能是(20,20)，那么计算出来的曲线方程就不一样了。

所以这里记录了你的屏幕密度，和作者的屏幕密度相比，然后放大相应的倍数就可以了。

从源码中我们可以看到这样两个属性

/** 
	   * Paths were generated at a 3px/dp density; this is the scale factor for different densities.
	   * 路径是在3px/dp密度下生成的，这将是不同屏幕密度的缩放因子
	   */
	  private final static float PATH_GEN_DENSITY = 3;
	
	  /** 
	   * Paths were generated with at this size for {@link DrawerArrowDrawable#PATH_GEN_DENSITY}.
	   * 在PATH_GEN_DENSITY密度下，将生成这个尺寸的路径 
	   */
	  private final static float DIMEN_DP = 23.5f;

这两个属性，就是作者的屏幕密度，和其密度下的尺寸大小，我们按比例缩放这个两个数字就可以了，下面会看到。

OK，初始化以后，开始设定曲线，我拿第一条横线做例子

// Top 第一条横线
	    first = new Path();
	    first.moveTo(5.042f, 20f);
	    //实现贝塞尔曲线,(x1,y1) 为控制点，(x2,y2)为控制点，(x3,y3) 为结束点
	    first.rCubicTo(8.125f, -16.317f, 39.753f, -27.851f, 55.49f, -2.765f);
	    second = new Path();
	    second.moveTo(60.531f, 17.235f);
	    second.rCubicTo(11.301f, 18.015f, -3.699f, 46.083f, -23.725f, 43.456f);	    
	    scalePath(first, density);
	    scalePath(second, density);
	    joinedA = new JoinedPath(first, second);
	
	    first = new Path();
	    first.moveTo(64.959f, 20f);
	    first.rCubicTo(4.457f, 16.75f, 1.512f, 37.982f, -22.557f, 42.699f);
	    second = new Path();
	    second.moveTo(42.402f, 62.699f);
	    second.cubicTo(18.333f, 67.418f, 8.807f, 45.646f, 8.807f, 32.823f);
	    scalePath(first, density);
	    scalePath(second, density);
	    joinedB = new JoinedPath(first, second);
	    topLine = new BridgingLine(joinedA, joinedB);

可以看到，首先new了一个first,然后moveTo()到一个位置（可想而知，这是状态1，a点的位置），然后调用rCubicTo()方法构造了贝塞尔曲线路径，这是一个三次贝塞尔曲线，关于rCubicTo()的具体用法，大家可以看api文档。这里（55.49f, -2.765f）对应的，就是状态2，a点的位置了，至于其他两个控制点，是由作者自己算出来的（计算方法上面已经说过了，就是模拟轨迹得到的）。

然后是second，其实就是状态2，到状态3了

接着调用scalePath()方法，其实是就是根据屏幕比例缩放了，上面已经提到过

/**
	   * Scales the paths to the given screen density. If the density matches the
	   * {@link DrawerArrowDrawable#PATH_GEN_DENSITY}, no scaling needs to be done.
	   * 根据屏幕密度扩大路径尺寸
	   */
	  private static void scalePath(Path path, float density) {
	    if (density == PATH_GEN_DENSITY) return;
	    Matrix scaleMatrix = new Matrix();
	    scaleMatrix.setScale(density / PATH_GEN_DENSITY, density / PATH_GEN_DENSITY, 0, 0);
	    path.transform(scaleMatrix);
	  }

最后，将两条路径合并成一个JoinedPath对象，由此可得，JoinedPath对象是保存了a从状态1到2的路径和a从状态2到3的路径

也即是JoinedPath保留了a的整个运动轨迹

/**
	   * Joins two {@link Path}s as if they were one where the first 50% of the path is {@code
	   * PathFirst} and the second 50% of the path is {@code pathSecond}.
	   * 合并两个路径，前50%为路径1，后50%为路径2
	   */
	  private static class JoinedPath {	
	    private final PathMeasure measureFirst;
	    private final PathMeasure measureSecond;
	    private final float lengthFirst;
	    private final float lengthSecond;
	
	    private JoinedPath(Path pathFirst, Path pathSecond) {
	    	//PathMeasure类用于提供路径上的点坐标
	    	measureFirst = new PathMeasure(pathFirst, false);
	    	measureSecond = new PathMeasure(pathSecond, false);
	    	lengthFirst = measureFirst.getLength();
	    	lengthSecond = measureSecond.getLength();
	    }
	
	    /**
	     * Returns a point on this curve at the given {@code parameter}.
	     * For {@code parameter} values less than .5f, the first path will drive the point.
	     * For {@code parameter} values greater than .5f, the second path will drive the point.
	     * For {@code parameter} equal to .5f, the point will be the point where the two
	     * internal paths connect.
	     * 根据参数(比例)返回曲线上的点
	     * 如果参数parameter小于0.5,使用第一条路径计算,大于0.5,使用第二条路径计算
	     * 等于0.5,该点为两条路径的连接点
	     */
	    private void getPointOnLine(float parameter, float[] coords) {
	      if (parameter <= .5f) {
	        parameter *= 2;
	        /*
	         * Pins distance to 0 <= distance <= getLength(), 
	         * and then computes the corresponding position and tangent. 
	         * Returns false if there is no path, or a zero-length path was specified, 
	         * in which case position and tangent are unchanged.
	         * 根据距离(该距离范围在0到路径长度之间),计算路径上相应点的坐标和tan三角函数值，分别存储在
	         * 后两个参数之中(后两个参数都是拥有两个元素的一维数组)	         	         
	         */
	        measureFirst.getPosTan(lengthFirst * parameter, coords, null);
	      } else {
	        parameter -= .5f;
	        parameter *= 2;
	        measureSecond.getPosTan(lengthSecond * parameter, coords, null);
	      }
	    }
	  }

有上面代码可以看到，JoinedPath中有两个PathMeasure对象，PathMeasure是android提供的，用来获取路径上点的坐标的一个类

例如我们有path路径a,长度是10（路径可能是曲线），我们用这个path创建一个PathMeasure对象，调用PathMeasure的getPosTan()方法，传入一个比例p(0-1),就可以得到在路径上，走了10*p距离的点的坐标。

那么对于a点，也就是说我们现在可以获得其轨迹上任意一点的坐标。

同理，对于b点

我们再次创建了first,second，然后合并出JoinedPath。

对于a,b两点的JoinedPath，我们又利用一个类来封装它们BridgingLine

topLine = new BridgingLine(joinedA, joinedB);

来看BridgingLine

/** 
	   * Draws a line between two {@link JoinedPath}s at distance {@code parameter} along each path.
	   * 根据两条路径上的点画一条直线 
	   */
	  private class BridgingLine {
	
	    private final JoinedPath pathA;
	    private final JoinedPath pathB;
	
	    private BridgingLine(JoinedPath pathA, JoinedPath pathB) {
	      this.pathA = pathA;
	      this.pathB = pathB;
	    }
	
	    /**
	     * Draw a line between the points defined on the paths backing {@code measureA} and
	     * {@code measureB} at the current parameter
	     * 根据当前参数，利用在两条路径上的两个点，画一条直线
	     */
	    private void draw(Canvas canvas) {
	      pathA.getPointOnLine(parameter, coordsA);
	      pathB.getPointOnLine(parameter, coordsB);
	      if (rounded) insetPointsForRoundCaps();
	      canvas.drawLine(coordsA[0], coordsA[1], coordsB[0], coordsB[1], linePaint);
	    }
	
	    /**
	     * Insets the end points of the current line to account for the protruding
	     * ends drawn for {@link Cap#ROUND} style lines.
	     * 
	     */
	    private void insetPointsForRoundCaps() {
	      vX = coordsB[0] - coordsA[0];
	      vY = coordsB[1] - coordsA[1];
	
	      magnitude = (float) Math.sqrt((vX * vX + vY * vY));
	      paramA = (magnitude - halfStrokeWidthPixel) / magnitude;
	      paramB = halfStrokeWidthPixel / magnitude;
	
	      coordsA[0] = coordsB[0] - (vX * paramA);
	      coordsA[1] = coordsB[1] - (vY * paramA);
	      coordsB[0] = coordsB[0] - (vX * paramB);
	      coordsB[1] = coordsB[1] - (vY * paramB);
	    }
	  }

BridgingLine没有太复杂的东西，其实就是提供了draw方法，用于画出a,b两点连成的横线。

到此位置，我们就可以画出a,b两点的横线了，但是a,b两个的坐标变化，是取决于parameter这个参数的

 pathA.getPointOnLine(parameter, coordsA);
	      pathB.getPointOnLine(parameter, coordsB);

那么这个参数又是什么决定的呢？

其实这个参数是我们主动传进去的，而这个参数大小，就等于侧拉抽屉的显示比例(当前显示面积，除以总面积)

这个是可想而知的，当这个侧拉抽屉被拉出来时，parameter应该等于1，表示去a,b点轨迹的最后一个点

而完全没有被拉出是，parameter应该等于0，表示去a,b点轨迹的第一个点

我们来看在外部怎么调用

final DrawerLayout drawer = (DrawerLayout) findViewById(R.id.drawer_layout);
        final ImageView imageView = (ImageView) findViewById(R.id.drawer_indicator);
        final Resources resources = getResources();
    
        drawerArrowDrawable = new DrawerArrowDrawable(resources);
        drawerArrowDrawable.setStrokeColor(resources.getColor(R.color.light_gray));
        imageView.setImageDrawable(drawerArrowDrawable);
    
        drawer.setDrawerListener(new DrawerLayout.SimpleDrawerListener() {
            @Override
            /*
             * Called when a drawer's position changes.//抽屉变化时调用
             * drawerView     The child view that was moved//被移动的子控件
             * slideOffset     The new offset of this drawer within its range, from 0-1//移动的比例 
             */
            public void onDrawerSlide(View drawerView, float slideOffset) {                
                offset = slideOffset;    
                // Sometimes slideOffset ends up so close to but not quite 1 or 0.
                //有时候移动停止时，slideOffset接近0或1,设置翻转
                if (slideOffset >= .995) {
                  flipped = true;
                  drawerArrowDrawable.setFlip(flipped);
                } else if (slideOffset <= .005) {
                  flipped = false;
                  drawerArrowDrawable.setFlip(flipped);
                }
            
                drawerArrowDrawable.setParameter(offset);                
        }
    });

从上面我们可以看到，我们为imageview设置了DrawerArrowDrawable对象，然后为DrawerLayout设置了一个监听器

对于这个监听器SimpleDrawerListener的onDrawerSlide()方法，当侧拉时，就会调用，传入slideOffset，也就是侧拉比例

可以知道slideOffset其实就是我们的parameter。

到此为止，这个箭头的效果就被我们实现了，接下只要在DrawerArrowDrawable的ondraw()方法里面，不断的绘制这三条曲线就好了

另外，这里做了一些近似处理，有时候移动停止时，slideOffset接近0或1,设置翻转

为什么要翻转呢，注意到，抽屉被拉出，和抽屉被缩入，箭头旋转的方向是不一样的，前者是0到180°，后者是180°到上360°

怎么实现呢，来看ondraw()方法就知道了

@Override 
	  public void draw(Canvas canvas) {
	    if (flip) {//是否翻转画布
	      canvas.save();
	      canvas.scale(1f, -1f, getIntrinsicWidth() / 2, getIntrinsicHeight() / 2);//中心点不变，y坐标对称
	    }
	
	    topLine.draw(canvas);
	    middleLine.draw(canvas);
	    bottomLine.draw(canvas);
	
	    if (flip) canvas.restore();
	  }

这个根据flip是否为真，从而决定是否翻转画布，翻转画布的效果的就是，使画布y坐标根据中心对称

对称以后，同样的效果0到180°,就会在画布上显示180°到上360°了，然后再讲画布恢复正常就可以了。

OK，DrawerArrowDrawable源码解析到这里就结束，看似简单的功能，却有复杂的逻辑。其实最复杂的逻辑在贝塞尔曲线的确定，本文提供了确定的思路，没有做具体的实现，大家可以参考控件原作者的文章。