【PA2014】【BZOJ3716】Muzeum

Description

吉丽的漫展有n件手办和m名警卫。建立平面直角坐标系，每个手办和警卫都可以看做一个点。警卫们的目光都朝着y轴负方向，且都有相同大小的视角。警卫可以看见自己视角内（包括边界上的点）的所有手办，不用考虑视线的遮挡。
你打算抢劫吉丽的漫展，但不可被警卫发现。为了实施这次抢劫计划，你可以事先贿赂某些警卫，让他们闭上眼睛。只要某件手办不在任何睁着眼睛的警卫的视野内，你就可以偷走它。你知道每件手办的价格，以及每位警卫需要接受多少钱的贿赂。你想知道自己的最大收益是多少。

Input

第一行两个整数n,m(1<=n,m<=200000)，分别表示手办的数量和警卫的数量。
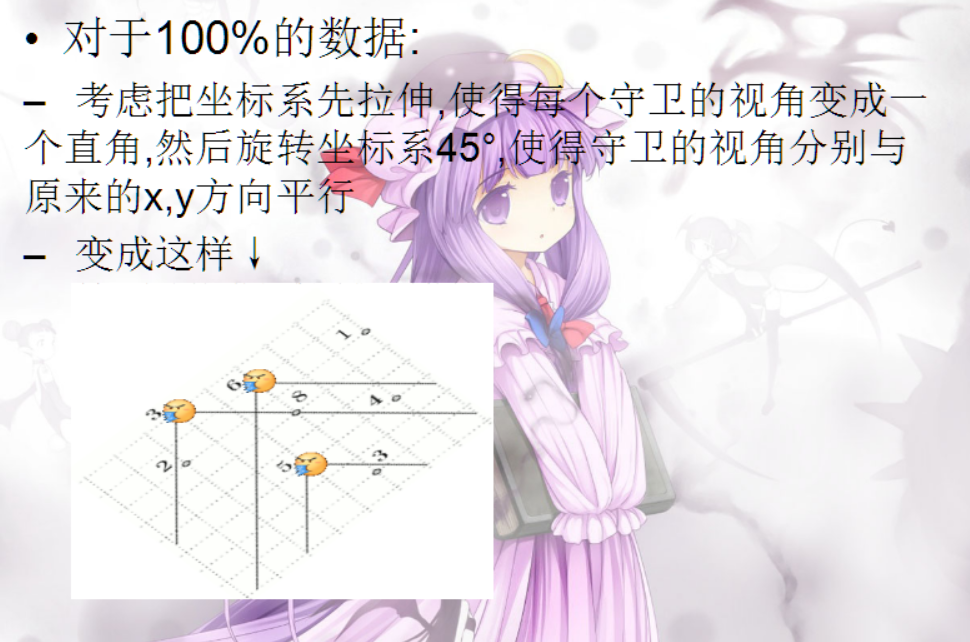
第二行两个整数w,h(1<=w,h<=10^9)，表示每个警卫的视角的一半的正切值是w/h。（见配图）
接下来n行，每行三个整数x[i],y[i],vi，表示手办的坐标为(x[i],y[i])，价格为v[i]。
接下来m行，格式同上，表示警卫的坐标为(x[i],y[i])，需接受贿赂的金额为v[i]。
保证每个点最多只有一个手办或一个警卫。

Output

输出仅一行表示最大收益。

Sample Input

5 3

2 3

2 6 2

5 1 3

5 5 8

7 3 4

8 6 1

3 8 3

4 3 5

5 7 6
Sample Output

6

样例解释：

贿赂3+6元，偷走2+8+4+1元，收益6元。

HINT

Source

鸣谢Jcvb

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<set>
#define MAXN 200010
#define GET (ch>='0'&&ch<='9')
#define LL long long
using namespace std;
int n,m;
LL w,h,x,y,v,ans;
struct Point
{
    LL x,y,v;
    bool operator <(const Point& a)const    {return x==a.x?y<a.y:x<a.x;}
}s[MAXN<<1];
struct node
{
    LL y,v;
    bool operator <(const node& a)const {return y<=a.y;}
};
void in(LL &x)
{
    char ch=getchar();x=0;LL flag=1;
    while (!GET)    flag=ch=='-'?-1:1,ch=getchar();
    while (GET) x=x*10+ch-'0',ch=getchar();x*=flag;
}
set<node>   S;
set<node>::iterator p;
int main()
{
    scanf("%d%d",&n,&m);in(w);in(h);
    for (int i=1;i<=n;i++)  in(x),in(y),in(v),x*=h,y*=w,s[i].x=x+y,s[i].y=y-x,s[i].v=v;
    for (int i=1;i<=m;i++)  in(x),in(y),in(v),x*=h,y*=w,s[i+n].x=x+y,s[i+n].y=y-x,s[i+n].v=-v;
    sort(s+1,s+n+m+1);
    for (int i=1;i<=n+m;i++)
        for (y=s[i].y,v=s[i].v;v;ans-=p->v,v+=p->v,S.erase(p))
        {
            p=S.lower_bound((node){y,0});
            if (p==S.end()||p->y!=y)
            {
                if (v>0)    {S.insert((node){y,v});ans+=v;break;}
                else    if (p==S.begin())   break;
                else    y=(--p)->y;
            }
        }
    cout<<ans<<endl;
}