机器学习之逻辑回归和softmax回归及代码示例

一、逻辑回归

在 机器学习之线性回归 中，我们可使用梯度下降的方法得到一个映射函数 $h_\theta(X)$ 来去贴近样本点，这个函数是对连续值的一个预测。

而逻辑回归是解决分类问题的一个算法，我们可以通过这个算法得到一个映射函数 $f：X → y$ ，其中 $X$ 为特征向量，$X = \{ x_0,x_1,x_2 ,…,x_n \}$，$y$ 为预测的结果。在逻辑回归这里，标签 $y$ 为一个离散值。

二、判定边界

当将训练集的样本以其各个特征为坐标轴在图中进行绘制时，通常可以找到某一个 判定边界 去将样本点进行分类。例如：

线性判定边界：

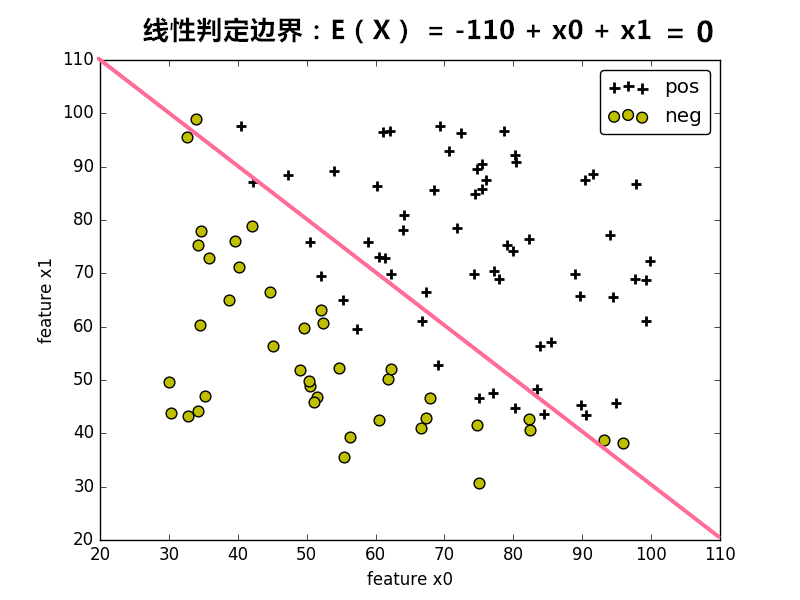
非线性判定边界：

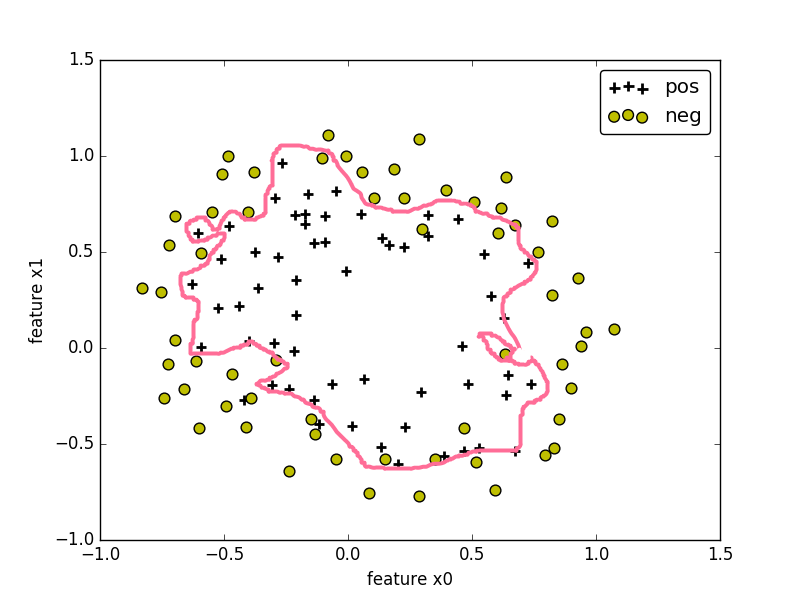
在图中，样本的标记类型有两种类型，一种为正样本，另一种为负样本，样本的特征 $x_0$ 和 $x_1$为坐标轴。根据样本的特征值，可将样本绘制在图上。

在图中，可找到某个 判定边界 来对不同标签的样本进行划分。根据这个判定边界，我们可以知道哪些样本是正样本，哪些样本为负样本。

因此我们可以通过学习得到一个方程 $E_\theta(X) = 0$ 来表示 判定边界，即 判定边界 为 $E_\theta(X) = 0$ 的点集。（可以看作是等高超平面）

$$E_\theta(X) = X^{T}\theta$$

其中 $\theta = \{ \theta_0,\theta_1,\theta_2,...,\theta_n\}$ ，为保留 $E_\theta(X) = 0$ 中的常数项，令特征向量 $X = \{ 1,x_1,x_2 ,…,x_n \}$。

为使得我们的边界可以非线性化，对于特征 $x_i$ 可以为特征的高次幂或相互的乘积。

对于位于判定边界上的样本，其特征向量 $X$ 可使得 Eθ(X)=0