算法-发明KMP算法的唐纳德·克努特是怎么想到失配函数next[j]的？

背景

字符串模式匹配，普通模式非常好理解，拿着模式串依次与主串做比较，知道完全匹配，但是这种算法，主串得不断地回溯，时间复杂度O(n*m)。

唐纳德·克努特

有没有降低时间复杂度的可能，唐纳德·克努特等人想到了一种办法不用使主串不停地回溯，而每次使模式串的某个字符与主串的待比较字符对齐，这个算法简称KMP。求解模式串的哪个字符该与这次比较的主串字符对齐，是KMP算法的核心，简称next函数或失配函数。这种算法求解复杂度降低到O（n+m）。

next函数语义

next[j]=k表达的意思是从模式串的 1~j-1 组成的子模式串，最长相同的前、后缀的长度为 k-1。举例说明，如下的字符串，next[6]=3，因为编号为6的字符c的最长前缀为编号为1的a ，编号为2的b 字符，最长后缀为编号为4的字符，编号为5的字符b，所以 k=3。

1	2	3	4	5	6	7	8
a	b	a	a	b	c	a	c

再看一下失配函数next[j]的严格定义，模式串字符的编码从1开始。

next函数分析

next 函数值仅取决于模式串本身而与相匹配的主串无关。从next函数的定义出发用递推的方法求next函数值。

由定义得知 next[1]=0，设next[j]=k，这表明在模式串中存在下列关系

"P1...Pk-1" = "Pj-k+1...Pj-1"

图形化显示（一条竖线表示一个字符）：

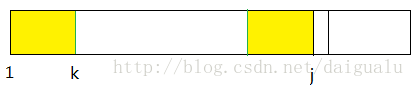
其中k为满足1 < k < j的某个值，并且不能存在k’ > k满足上个等式。此时 next[j+1]=? 分两种情况讨论，

1）若 Pk = Pj ，则 next[j+1] = next[j] + 1 ，即 k + 1 ，如下图显示：