改革春风吹满地,又到求职高峰期。简历撒遍无人理,自信绝不受打击。在浏览过各大软件公司面经之后,我发现一道很常见也很有趣的编程题目:
要将100元兑换为1元、5元、10元的零钱,请问有多少种兑换方法?
如果您跟我一样,喜欢挑战难度,愿意将问题改为“此题有多少种解法?”,那么本文应该会合您的口味。
方法一:
以程序员的眼光来看,我拿到这个问题的第一感觉就是递归。对于这100元,先用10元的零钱来换:
100 = 0*10 + R0 = 1*10 + R1 = 2*10 + R2 … = 10*10 + R10
其中RN是换完后剩余的钱数。然后再对RN用5元的零钱来换,以此类推。写成python程序如下:
# (global value) the list of coins.
# the order is arbitary.
COIN_LIST = (1, 5, 10)
def num_of_changes(money, coin_index):
current_coin = COIN_LIST[coin_index]
# if it is the last kind of coins,
# stop recursion and exame whether
# remaining money is divisible by this kind of coins.
if coin_index == len(COIN_LIST) - 1:
return int(money % current_coin == 0)
count = 0
# construct recursive chain by increasing coin_index,
# which means using different kinds of coins to parition
# the remaining money.
while money >= 0:
count += num_of_changes(money, coin_index + 1)
money -= COIN_LIST[coin_index]
return count
=========================
# usage:
>>> print num_of_changes(100, 0)
>>> 121
值得一提的是,COIN_LIST中的零钱种类不必排序,并不影响结果。num_of_changes函数相当通用,可以应付各种总钱数以及各类零钱的兑换。
方法二:
其实有初中以上数学背景的人,会立刻将此问题转化为求如下不定方程的非负整数解:
1*x + 5*y + 10*z = 100 (x,y,z >= 0)
认为下面将要介绍的是暴力穷举法(brute-force method)的读者们,请不要跳过此处。这是经典的线性丢番图方程(Linear Diophantine Equations),其标准解法为“扩展欧几里德算法”(Extended Euclidean Algorithm)。要解释这个算法就不得不提到欧几里德大人在公元前300年写的《几何原本》一书,其中记载了一种求两个数的最大公约数 (Greatest common divisor) 的算法。别看它古老,此算法的效率奇高,目前还无人能出其右(注:有些公司居然会在面试中考GCD算法,典型的背书题,实在无聊)。此方法也叫辗转相除法,其可行性依赖于恒等式:
gcd(a, b) == gcd(a mod b, b)
例如求GCD(1234, 567),分解步骤为:
(a) 1234 = 2 * 567 + 100 (b) 567 = 5 * 100 + 67 (c) 100 = 1 * 67 + 33 (d) 67 = 2 * 33 + 1 (e) 33 = 33 * 1 + 0
所以 GCD(1234, 567) = GCD(33, 1) = 1。但这个方法与解线性丢番图方程有什么联系呢?请考虑方程:
1234*x + 567*y = 1
我们将步骤(a)至(d)的运算倒推回去:
(d') 1 = 67 – 2 * 33 (c') = 67 – 2 * (100 – 1 * 67) (整理) = -2 * 100 + 3 * 67 (b') = -2 * 100 + 3 * (567 – 5 * 100) (整理) = 3 * 567 – 17 * 100 (a') = 3 * 567 – 17 * (1234 – 2 * 567) (整理) = -17 * 1234 + 37 * 567
注意到了吗? {x0 = -17, y0 = 37} 就是原方程的一个解。那么是否还有其他整数解呢?善用暴力穷举法的兄弟们请出手吧。你会很快发现规律:
{xn = -17 + 567*N, yn = 37 – 1234*N},其中N为任意整数
而对于更具一般性的方程:
1234*x + 567*y = k
其解系为
{ X = k*xn , Y = k*yn }, 其中k为非零任意整数
可以证明,用此方法,总是可以找到形如:
a*x + b*y = gcd(a, b) (假设a,b都不为0)
的丢番图方程的全部整数解:
{xn = x0 + b*N, yn = y0 – a*N},其中N为任意整数
而对于更一般的方程,
a*x + b*y = c (假设a,b都不为0)
设d = gcd(a, b),若c是d的整数倍,则全部整数解为:
{xn = c/d * x0 + b/d * N, yn = c/d * y0 – a/d * N},其中N为任意整数
若c不是d的整数倍,则此方程无整数解。值得注意的是,只要我们能找到此方程的一个解,那么就可以通过上式轻松的列举出无穷多个整数解,而且是全部的整数解。
对于多元的线性丢番图方程,只需将其分为一个个二元线性丢番图方程,各个击破再合并起来即可。例如:
a*x + b*y + c*z = d
不妨假设gcd(a,b,c)能够整除d,否则无解。先求解子方程:
a*X + b*Y = g = gcd(a,b)
之前已经提到,其全部整数解就是:
{Xn = X0 + b*N, Yn = Y0 – a*N},其中N为任意整数
下一步求解:
g*w + c*z = d
由于gcd(g, c) = gcd(a, b, c) = f,且f可以整除d,所以此方程一定有解:
{wm = d/f * w0 + c/f * M, zm = c/f * z0 – g/f * M},
其中M为任意整数, w0和z0为方程g*w + c*z = f的一个特解。将Xn, Yn带入得:
(a*Xn + b*Yn)*wm + c*zm = a*(Xn*wm) + b*(Yn*wm) + c*zm = d
所以:
{xn,m = Xn*wm , yn,m = Yn*wm , zn,m = zm } 其中N,M为任意整数.
就原问题1*x + 5*y + 10*z = 100而言,读者可以自己验证:
xn,m = (100 + 10*M)(1+5*N)
yn,m = -(100 + 10*M)*N
zn,m = -M
由于{x, y, z}为非负整数,所以要求出到底有多少个这样的解,则还是需要使用暴力穷举法。虽然绕了一大圈,解法退回到最原始的模样(请勿拍砖),但还是希望您能从多变量一般线性丢番图方程(Multiple-variable generalized diophantine equation)的解法中得到启示。
方法三:
| n | 划分方式 | p(n) |
| 1 | 1 | 1 |
| 2 | 2, 1+1 | 2 |
| 3 | 3, 2+1, 1+1+1 | 3 |
| 4 | 4, 3+1, 2+2, 2+1+1, 1+1+1+1 | 5 |
| 5 | 5, 4+1, 3+2, 3+1+1, 2+2+1, 2+1+1+1, 1+1+1+1+1 | 7 |
欧拉(Euler)在1748年前后对p(n)进行了的理论研究,并发现了如下生成函数:
式子左侧的无穷乘积可以展开成右侧的幂级数形式,其中级数各项的系数“生成”了p(n)。下面给出一个不太严格的示意性证明。考虑将1 / (1 – xn) 展开成幂级数:
当我们将左侧各式相乘,并仔细的对右侧相同指数的各项进行合并时,我们就会发现p(n)的确被生成出来了。例如对于x5:
其中每一项分别对应于5的一种划分方式:1+1+1+1+1,1+1+1+2,1+1+3,1+4,1+2+2,2+3,5。更一般的说,xa*b 意味着某一划分方式中的b个a相加,而每一个1 / (1 – xa)都对应于一种划分时可以选择的单位。所以,对于将100元兑换成1元、5元、10元的问题,我们可以通过求解下式的幂级数展开来获得,其中x100项的系数就是答案:
方法四:
可以想象,p(n)的值会随着n的增大而迅速膨胀,比如p(100) = 190,569,292。膨胀的速度到底有多快?这里给出一个p(n)的渐近公式:
上式由Hardy和Ramanujan在1917-1918年利用了复变函数论的方法得出。类似的,还记得大学时讲的斯特林公式吗?就是关于阶乘的渐进公式:
这两个渐进公式当n趋于∞时,约等号将变为等号。值得一提的是,式子的左侧都是整数,而右侧却包含了无理数:圆周率、自然对数、开方。真是太不可思议了!圆周率是怎么跟划分方式和阶乘扯到一块儿去的?也许这就是在我们离开这个世界的时候,第一个要询问上帝的事情。
对于像Mathematica语言这样的计算机代数系统,且当n比较小的时候,使用[方法三]求解还是可行的,但对于比较大的n,这绝非易事。所幸函数p(n)有一个由欧拉(Euler)发现的重要的递归公式:
p(n) = p(n-1) + p(n-2) - p(n-5) - p(n-7) + p(n-12) + p(n-15) - p(n-22) – p(n-26) + …,
并约定当n < 0时p(n) = 0,以及p(0) = 1。
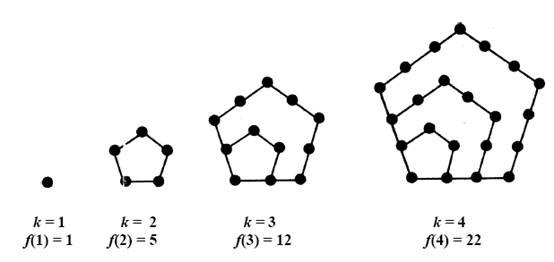
这个公式神秘之处在于其中出现的常数1, 2, 5, 7, 12, 15…,它们在数论中有一个形象的名字,五角数(pentagonal numbers)。五角数的几何定义来自于一个不断扩大的五边形,其中结点的数目就是五角数,其通式为:f(k) = k(3k – 1) / 2。通过数一数下图中黑点的数目就可以验证这个公式。
而对于剩下来的常数:2,7,15,26,我们可以定义负五角数:f(-k) = k(3k + 1) / 2。可惜它的几何意义目前还不得知。有了五角数的定义,我们就可以将Euler的递归公式改写为:
证明上式需要用到欧拉五角数定理(Euler's pentagonal number theorem),已经超出本文范围,但由于证明本身很有趣,我们在此给出一个概要。从下式出发:
读者可以通过乘出左侧前面几项来发现它跟五角数的关系:
注意到[方法三]中的Euler生成函数公式,正好是上式的倒数,所以:
展开后按x合并同类项得到:
由于x的取值是任意的,所以要想等式成立,必须x各项系数都为0。从而得到欧拉递归公式:
回到我们的分钱问题,同样可以用类似的办法得到。我们设q(n)为将n划分为1,5,10的函数,并令n < 0时,q(n) < 0;q(0) = 1则:
写成python代码:
q_map = {0:1}
def q(n):
if n < 0:
return 0
if n in q_map:
return q_map[n]
r = q(n-1)+q(n-5)+q(n-10)-q(n-6)-q(n-11)-q(n-15)+q(n-16)
q_map[n] = r
return r
# usage:
====================
>>> print q(100)
>>> 121
有心的读者可能注意到了 6 = 1+5, 11 = 1+10, 15 = 5+10, 16 = 1+5+10。就像划分方式与五角数之间的奇特联系一样,这里又意味着什么呢?尝试验证一下你的猜想,解释在p(n)的递归关系式中为何p(n-3), p(n-4), p(n-6)等项并未出现?很神奇不是吗?也许正是这些不期而遇的、意料不到的相关性,给看似枯燥的数学研究增添了无穷的乐趣。










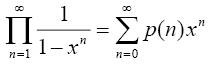
![clip_image002[12] clip_image002[12]](https://p-blog.csdn.net/images/p_blog_csdn_net/drshenlei/627110/o_clip_image002%5B12%5D_thumb.jpg)
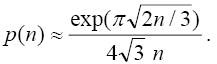
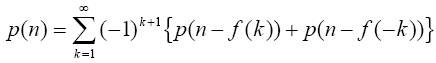
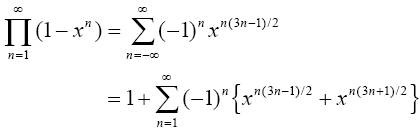
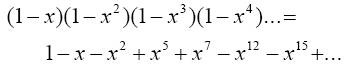
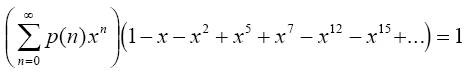
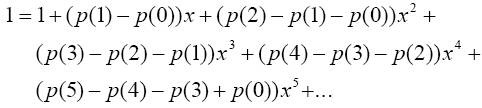
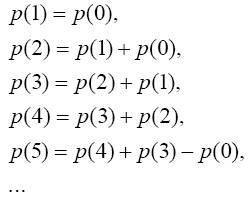
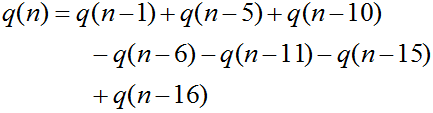














 1783
1783

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








