一,图的遍历基本理论
首先定义图的遍历(Traversing Graph):指从图中某一顶点出发访问图中其余顶点,且使每个顶点仅被访问一次。有两种常用的方法可用来搜索图:即深度优先搜索和广度优先搜索。它们最终都会到达所有连通的顶点。深度优先搜索通过栈来实现,而广度优先搜索通过队列来实现。
1,深度优先图搜索
(DFS,Depth-First-Search):
下面图中的动态图显示了深度优先搜索顶点被访问的顺序。
为了实现深度优先搜索,首先选择一个起始顶点并需要遵守三个规则:
(1) 如果可能,访问一个邻接的未访问顶点,标记它,并把它放入栈中。
(2) 当不能执行规则1时,如果栈不空,就从栈中弹出一个顶点。
(3) 如果不能执行规则1和规则2,就完成了整个搜索过程。
伪代码:
<span style="font-family:Times New Roman;font-size:18px;">procedure dfs(vertex v)
{
mark v as visited //标记顶点为已访问
for each w adjacent to v //将邻顶点变成新的当前顶点
{
if w unvisited//若这个新的当前节点没有被访问过
{
dfs(w) //递归调用
}
}
}</span>
2,广度优先图搜索
(BFS,Breadth First Search):
在深度优先搜索中,算法表现得好像要尽快地远离起始点似的。相反,在广度优先搜索中,算法好像要尽可能地靠近起始点。
它首先访问起始顶点的所有邻接点,然后再访问较远的区域。它是用队列来实现的。
下面图中的数字显示了广度优先搜索顶点被访问的顺序。
实现广度优先搜索,也要遵守三个规则:
(1) 访问下一个未来访问的邻接点,这个顶点必须是当前顶点的邻接点,标记它,并把它插入到队列中。
(2) 如果因为已经没有未访问顶点而不能执行规则1时,那么从队列头取一个顶点,并使其成为当前顶点。
(3) 如果因为队列为空而不能执行规则2,则搜索结束。
伪代码:
procedure BFS(vertex s)
{
create a queue Q //创建一个队列
enqueue s onto Q //顶点s进队
mark s as visited //
while Q is not empty
{
dequeue a vertex from Q into v
for each w adjacent to v
{
if w unvisited
{
mark w as visited
enqueue w onto Q
}
}
}
}
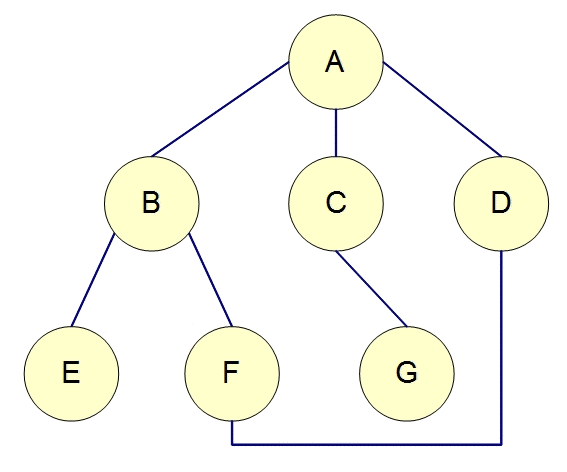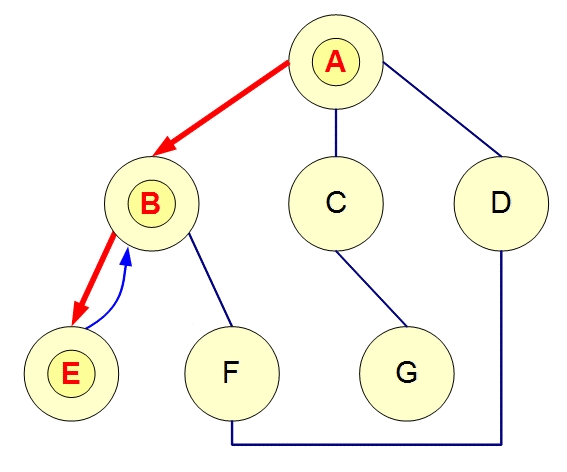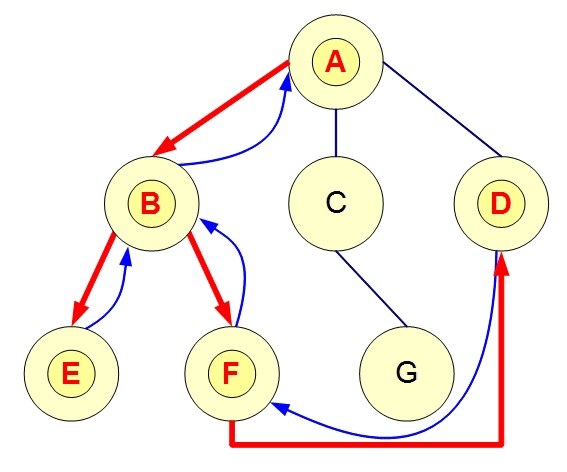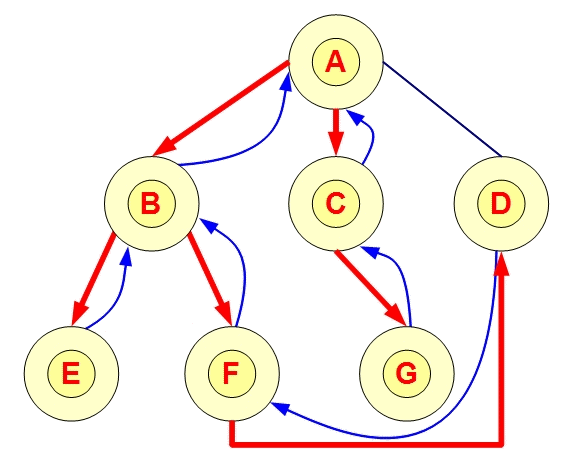
3,上文例图中,两者的搜索区别:
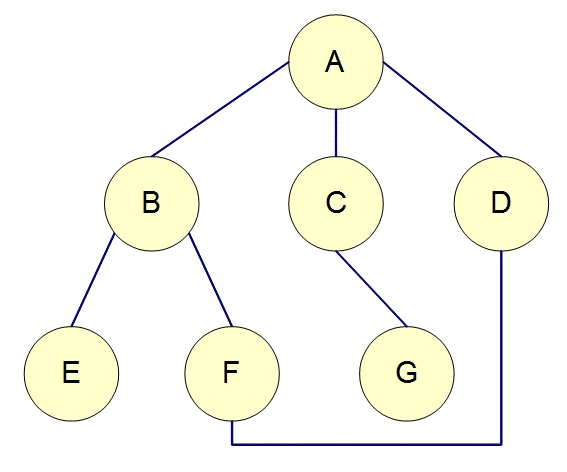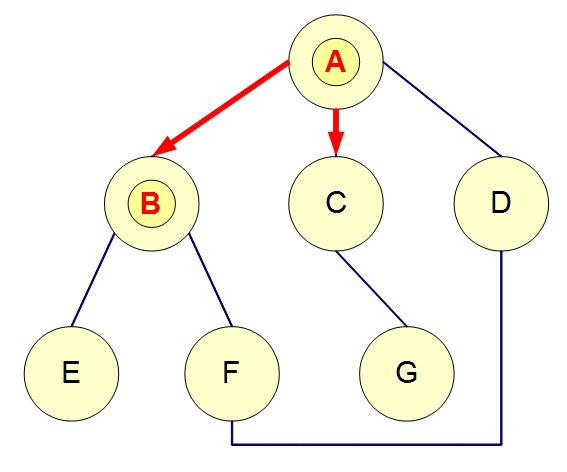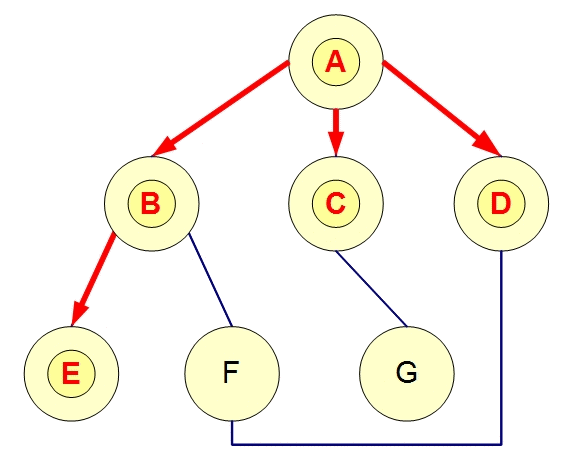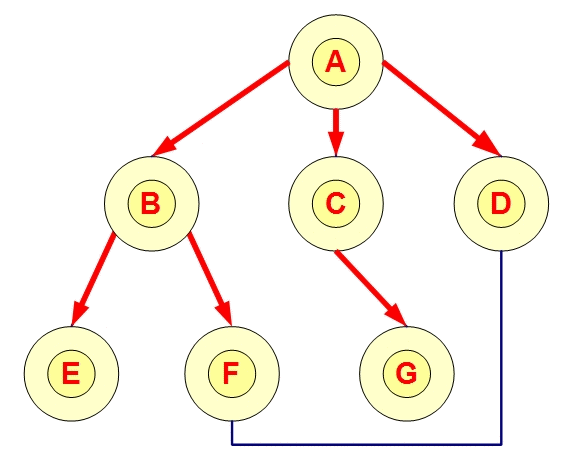
广度优先搜索顺序应该为: A-B-C-D-E-F-G
深度优先搜索顺序应该为:A-B-E-F-D-C-G
文字描述两者区别:
广度优先每次遍历完某一个顶点的所有相邻顶点,然后再从这些相邻额顶点中在选择一个顶点作为初始顶点重复上面的过程。
二,C++模板实现
(本程序构造的是一棵树,无任何回路)
1,Graph.h的代码如下:
#include "stdafx.h"
#include "iostream"
#include "queue"
using namespace std;
template<class DistType/*边的权值的类型*/>
class Edge//边的定义
{
public:
Edge(int dest, DistType weight)
{
m_nposTable=dest;
m_distWeight=weight;
m_pnext=NULL;
}
~Edge()
{
}
public:
int m_nposTable;//该边的目的顶点在顶点集中的位置
DistType m_distWeight;//边的权重值
Edge<DistType> *m_pnext;//下一条边(注意不是下一个顶点,因为m_nposTable已经知道了这个顶点的位置)
};
//声明
template<class NameType/*顶点集名字类型*/, class DistType/*距离的数据类型*/> class Graph;
template<class NameType/*顶点集名字类型*/, class DistType/*距离的数据类型*/>
class Vertex//顶点的定义
{
public:
Vertex()
{
padjEdge=NULL;
m_vertexName=0;
}
~Vertex()
{
Edge<DistType> *pmove = padjEdge;
while (pmove)
{
padjEdge = pmove->m_pnext;
delete pmove;
pmove = padjEdge;
}
}
private:
friend class Graph<NameType,DistType>;//允许Graph类任意访问
NameType m_vertexName;//顶点中的数据内容
Edge<DistType> *padjEdge;//顶点的邻边
};
template<class NameType/*顶点集名字类型*/, class DistType/*距离的数据类型*/>
class Graph
{
public:
Graph(int size = m_nDefaultSize/*图顶点集的规模*/)
{
m_pVertexTable = new Vertex<NameType, DistType>[size]; //为顶点集分配内存
if (m_pVertexTable == NULL)
{
exit(1);
}
m_numVertexs=0;
m_nmaxSize=size;
m_nnumEdges=0;
}
~Graph()
{
Edge<DistType> *pmove;
for (int i=0; i < this->m_numVertexs; i++)
{
pmove = this->m_pVertexTable[i].padjEdge;
if (pmove){
this->m_pVertexTable[i].padjEdge = pmove->m_pnext;
delete pmove;
pmove = this->m_pVertexTable[i].padjEdge;
}
}
delete[] m_pVertexTable;
}
int GetNumEdges()
{//获得边的数目
return m_nnumEdges/2;
}
int GetNumVertexs()
{//获得顶点数目
return m_numVertexs;
}
bool IsGraphFull() const
{ //图满的?
return m_nmaxSize == m_numVertexs;
}
//在顶点集中位置为v1和v2的顶点之间插入边
bool InsertEdge(int v1, int v2, DistType weight=m_Infinity);
//插入顶点名字为vertex的顶点
bool InsertVertex(const NameType vertex);
//打印图
void PrintGraph();
//顶点v到其他各个顶点的最短路径(包括自身)
void Dijkstra(int v, DistType *shotestpath);
//获取顶点集中位置为v1和v2的顶点之间边的权重值
DistType GetWeight(int v1, int v2);
//获得在顶点集中的位置为v的顶点的名字
NameType GetVertexValue(int v);
//用该顶点的名字来寻找其在顶点集中的位置
int GetVertexPosTable(const NameType vertex);
//深度搜索优先
void DFS(int v, int *visited);
void DFS();
//广度优先搜索
void BFS(int v, int *visited);
void BFS();
//获取第v个顶点的名字(或者说内容)
NameType GetVertexName(int v);
//获得顶点v的第一个相邻顶点,如果没有就返回-1
int GetFirst(int v);
//获得顶点v1的邻点v2后的邻点
int GetNext(int v1, int v2);
private:
Vertex<NameType, DistType> *m_pVertexTable; //顶点集
int m_numVertexs;//图中当前的顶点数量
int m_nmaxSize;//图允许的最大顶点数
static const int m_nDefaultSize = 10; //默认的最大顶点集数目
static const DistType m_Infinity = 65536; //边的默认权值(可以看成是无穷大)
int m_nnumEdges;//图中边的数目
};
//返回顶点vertexname在m_pVertexTable(顶点集)中的位置
//如果不在顶点集中就返回-1
template<class NameType, class DistType>
int Graph<NameType, DistType>::GetVertexPosTable(const NameType vertexname)
{
for (int i=0; i < this->m_numVertexs; i++)
{
if (vertexname == m_pVertexTable[i].m_vertexName)
{
return i;
}
}
return -1;
}
//打印图中的各个顶点及其链接的边的权重
template<class NameType, class DistType>
void Graph<NameType, DistType>::PrintGraph()
{
Edge<DistType> *pmove;
for (int i=0; i<this->m_numVertexs; i++)
{
cout << this->m_pVertexTable[i].m_vertexName << "->";
pmove = this->m_pVertexTable[i].padjEdge;
while (pmove)
{
cout << pmove->m_distWeight << "->" << this->m_pVertexTable[pmove->m_nposTable].m_vertexName << "->";
pmove = pmove->m_pnext;
}
cout << "NULL" << endl;
}
}
//获得在顶点集中的位置为v的顶点的名字
template<class NameType, class DistType>
NameType Graph<NameType, DistType>::GetVertexValue(int v)
{
if (v<0 || v>=this->m_numVertexs)
{
cerr << "查找的顶点位置参数有误,请检查!" <<endl;
exit(1);
}
return m_pVertexTable[v].m_vertexName;
}
//返回顶点v1和v2之间的边权值,
//如果没有直接相连(即不是一条边直接相连)则返回无穷大
template<class NameType, class DistType>
DistType Graph<NameType, DistType>::GetWeight(int v1, int v2)
{
if (v1>=0 && v1<this->m_numVertexs && v2>=0 && v2<this->m_numVertexs)
{
if (v1 == v2)
{
return 0;
}
Edge<DistType> *pmove = m_pVertexTable[v1].padjEdge;
while (pmove)
{
if (pmove->m_nposTable == v2)
{
return pmove->m_distWeight;
}
pmove = pmove->m_pnext;
}
}
return m_Infinity;
}
//顶点依次插入到分配好的顶点集中
template<class NameType, class DistType>
bool Graph<NameType, DistType>::InsertVertex(const NameType vertexname)
{
if (IsGraphFull())
{
cerr<<"图已经满,请勿再插入顶点!"<<endl;
return false;
}else
{
this->m_pVertexTable[this->m_numVertexs].m_vertexName = vertexname;
this->m_numVertexs++;
}
return true;
}
//在顶点集位置为v1和v2的顶点之间插入权值为weght的边(务必保持输入的准确性,否则.....)
template<class NameType, class DistType>
bool Graph<NameType, DistType>::InsertEdge(int v1, int v2, DistType weight)
{
if (v1 < 0 && v1 > this->m_numVertexs && v2 < 0 && v2 > this->m_numVertexs)
{
cerr<<"边的位置参数错误,请检查! "<<endl;
return false;
}
else
{
Edge<DistType> *pmove = m_pVertexTable[v1].padjEdge;
if (pmove == NULL)//如果顶点v1没有邻边
{ //建立顶点v1的第一个邻边(该邻边指明了目的顶点)
m_pVertexTable[v1].padjEdge = new Edge<DistType>(v2, weight);
m_nnumEdges++;//图中边的数目
return true;
}else//如果有邻边
{
while (pmove->m_pnext)
{
pmove = pmove->m_pnext;
}
pmove->m_pnext = new Edge<DistType>(v2, weight);
m_nnumEdges++;//图中边的数目
return true;
}
}
}
template<class NameType, class DistType>
void Graph<NameType, DistType>::Dijkstra(int v, DistType *shPath)
{
int num =GetNumVertexs();
int *visited = new int[num];
for (int i=0; i < num; i++)
{//初始化
visited[i] = 0;//未访问
shPath[i] = this->GetWeight(v, i);//顶点v(当前中间点)到各个相邻顶点的边权值,其他情况返回无穷大
}
visited[v] = 1;//第v个顶点初始化为被访问,并以他为中点点开始找最短路径
for (int i = 1; i < num; i++)
{
DistType min = this->m_Infinity;
int u=0;
//寻找新的中间点u,依据就是数组中权值最小的那个点的位置(且没被访问过)
for (int j=0; j < num; j++)
{
if (!visited[j])
{
if (shPath[j]<min)
{
min = shPath[j];//获得当前shPath数组中的最小边权重
u = j;//用u来记录获取最小值时的顶点位置,即新的中间点
}
}
}
visited[u] = 1;//已经确定的最短路径
//以u为中间点寻找顶点v到顶点w的最短路径
for (int w=0; w < num; w++)
{
DistType weight = this->GetWeight(u, w);//顶点u(当前中间点)到各个相邻顶点的边权值,其他情况返回无穷大
if (!visited[w] && weight != this->m_Infinity )
{
if ( shPath[u]+weight < shPath[w] )
{
shPath[w] = shPath[u] + weight;//更新顶点v到w的最短路径值
}
}
}
}
delete[] visited;
}
//获得顶点v1的邻点v2后的邻点
template<class NameType, class DistType>
int Graph<NameType, DistType>::GetNext(int v1, int v2)
{
if (-1 != v1)
{
Edge<DistType> *pmove = this->m_pVertexTable[v1].padjEdge;
while (NULL != pmove->m_pnext)
{
if (pmove->m_nposTable==v2)
{
return pmove->m_pnext->m_nposTable;
}
pmove = pmove->m_pnext;
}
}
return -1;
}
//从第v个顶点开始深度遍历
template<class NameType, class DistType>
void Graph<NameType, DistType>::DFS(int v, int *visited)
{
cout << "->" << this->GetVertexName(v);
visited[v] = 1;
int firstVertex = this->GetFirst(v);//获得顶点v的第一个相邻顶点,若没有则返回-1
while (-1 != firstVertex)
{
if (!visited[firstVertex])//如果没有访问过
{
cout << "->" << this->GetWeight(v, firstVertex);//获得顶点v及其邻点firstVertex之间的权值
DFS(firstVertex, visited);
}
firstVertex = this->GetNext(v, firstVertex);//获得顶点v的邻点firstVertex后的邻点,如果没有就返回-1
}
}
template<class NameType, class DistType>
void Graph<NameType, DistType>::DFS()
{
int *visited = new int[this->m_numVertexs];
for (int i=0; i<this->m_numVertexs; i++)
{
visited[i] = 0;
}
cout << "head";
DFS(0, visited);//从第一个顶点开始遍历
cout << "--->end";
}
template<class NameType, class DistType>
void Graph<NameType, DistType>::BFS()
{
int *visited = new int[this->m_numVertexs];
for (int i=0; i<this->m_numVertexs; i++)
{
visited[i] = 0;
}
cout << "head";
BFS(0, visited);//从第一个顶点开始遍历
cout << "--->end";
}
//从第v个顶点开始广度遍历
template<class NameType, class DistType>
void Graph<NameType, DistType>::BFS(int v, int *visited)
{
cout << "->" << this->GetVertexName(v);
visited[v]=1;
queue<int> que;//=new queue<int>[this->GetNumVertexs()];
que.push(v);//进队(队列的末端)
while (!que.empty())
{
v=que.front();//出队首元素
que.pop();//删除队首元素
int firstvertex=GetFirst(v);
while(firstvertex != -1)
{
if (!visited[firstvertex])
{
cout << "->" << this->GetWeight(v, firstvertex);//获得顶点v及其邻点firstVertex之间的权值
que.push(firstvertex);
visited[firstvertex]=1;
cout << "->" << this->GetVertexName(firstvertex);
}
firstvertex=GetNext(v,firstvertex);
}
}
}
//获得在顶点集中的位置为v的顶点的名字
template<class NameType, class DistType>
NameType Graph<NameType, DistType>::GetVertexName(int v)
{
if (v<0 || v>=this->m_numVertexs)
{
cerr << "查找的顶点位置参数有误,请检查!" <<endl;
exit(1);
}
return m_pVertexTable[v].m_vertexName;
}
//获得顶点v的第一个相邻顶点,如果没有就返回-1
template<class NameType, class DistType>
int Graph<NameType, DistType>::GetFirst(int v)
{
if (v<0 || v>=this->m_numVertexs)
{
return -1;
}
Edge<DistType> *ptemp = this->m_pVertexTable[v].padjEdge;
return m_pVertexTable[v].padjEdge ? m_pVertexTable[v].padjEdge->m_nposTable : -1;
}2,主程序代码如下:
// ConsoleAppMyGraph.cpp : 定义控制台应用程序的入口点。
//
#include "stdafx.h"
#include "Graph.h"
#include <iostream>
using namespace std;
int _tmain(int argc, _TCHAR* argv[])
{
Graph<char *, int> graph(7);
char *vertex[7] = {"【地大】", "【武大】", "【华科】", "【交大】", "【北大】", "【清华】", "【复旦】"};//顶点集
for (int i=0; i<7; i++)
{
graph.InsertVertex(vertex[i]);
}
cout<<"一,图的初始化(邻结表存储):======================================"<<endl;
graph.PrintGraph();
cout<<"图中顶点的数目:"<<graph.GetNumVertexs()<<endl;
cout <<endl;
int edge[][3] = {{0, 1, 43}/*地大到武大的距离*/, {0, 2, 12}, /*{1, 2, 38}*/ /*{2, 3 ,1325}*/
/*{3, 6, 55}*/ {4, 5, 34}, /*{4, 6, 248}*/{0,3,400},{2,6,314},{2,4,37}}; //分配距离
int len=sizeof(edge)/sizeof(edge[0]);
for (int i=0; i < len; i++)
{
graph.InsertEdge(edge[i][0], edge[i][1], edge[i][2]);
graph.InsertEdge(edge[i][1], edge[i][0], edge[i][2]);
}
cout<<"二,添加边后的图(无向图):=================================="<<endl;
graph.PrintGraph();
cout<<"图中边的数目(实际上是所示边数的两倍,因为是双向的):"<<graph.GetNumEdges()<<endl;
cout <<endl;
cout<<"三,Dijkstra法最短路径为:=========================="<<endl;
int shortestPath[7];//存储Dijkstra算法最短路径值
graph.Dijkstra(0, shortestPath);
for (int i=0; i<7; i++)
{
cout << graph.GetVertexValue(0) << "--->" << graph.GetVertexValue(i)
<< ": " << shortestPath[i] <<endl;
}
cout<<endl;
cout<<"四,图的遍历:=========================="<<endl;
cout<<"1,DFS深度优先遍历结果:"<<endl;
graph.DFS();
cout<<endl<<endl;
cout<<"2,BFS广度优先遍历结果:"<<endl;
graph.BFS();
cout<<endl<<endl;
system("color 0A");
system("pause");
return 0;
}3,测试结果如下:
参考资源
【1】《算法导论》
【2】《维基百科》
【3】http://www.cnblogs.com/rollenholt/archive/2012/04/09/2439055.html






















 6654
6654

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








