| 文章详细介绍了使用matlab实现无约束和约束最优化问题的方法和程序,及使用方法,包含黄金分割法、最速下降法、牛顿法、外点法、内点法,例子丰富. |
注:该文章首先在本人新浪博客发布,后来迁移过来公式图片就这样了,介意者可以查看:
1.某文库
2.新浪博客
报告按照优化方法:黄金分割法、最速下降法、牛顿法、外点法、内点法的顺序叙述,分为两篇,第一篇为无约束优化,第二篇为约束优化.
第一篇 无约束优化
1. 黄金分割法
黄金分割法又称0.618法,其基本思想是试探点函数值的比较,使含极小点的搜索区间不断缩小.该方法仅需计算函数值,适用范围广,使用方便.由于该方法思想简单,在此不给出具体算法流程,仅介绍思想和matlab实现的程序.
1.1 思想
在搜索区间内插入点
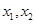
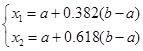
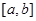
的大小,若
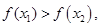

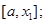
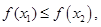
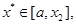
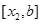
1.2 实现及结果
采用matlab 2011a实现,命名为golden,具体程序见附录golden.m文件.
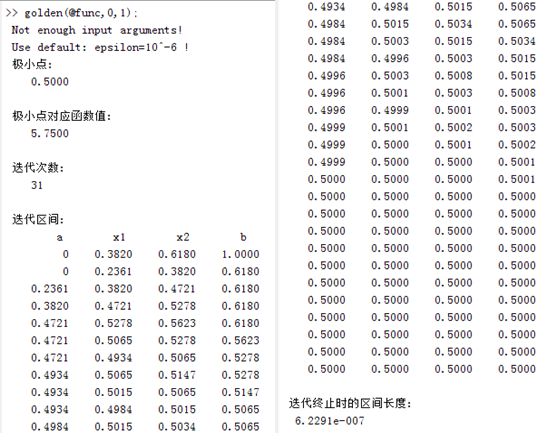
该程序的使用方法,请参见附录中golden.m文件中绿色部分,下面给出程序运行结果,其中目标函数为: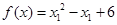
图1-1-1 黄金分割法运行结果
2. 最速下降法
最速下降法是求解无约束优化问题最简单和最古老的方法之一,时至今日已不再具有实用性,但它是研究其它无约束优化算法的基础.
最速下降法适合解决下述优化问题:
2.1 思想
无约束优化问题下降类算法的一般框架是,用不同的方式确定搜索方向和搜索步长,就得到不同的算法,最速下降法采用负梯度方向
作为搜索方向,由于该方向是函数值下降最快的方向,故称为最速下降法.
2.2 算法
最速下降法的算法如下:
2.3 实现及结果
采用matlab 2011a实现,具体程序见附录fast.m文件.
下面以上机题第一题为例介绍具体使用方法:
上机题1的优化目标函数为
首先分别建立两个文件即目标函数文件func.m和对应梯度文件gfunc.m内容分别如下:
func.m文件
function f = func( x )
% ---------------最速下降法、牛顿法用------------
f=(x(1)+10*x(2))^2+5*(x(3)-x(4))^2+(x(2)-2*x(3))^4+10*(x(1)-x(4))^4;
gfunc.m文件
function gf = gfunc( x )
%目标函数的梯度
gf=[2*(x(1)+10*x(2))+40*(x(1)-x(4))^3
20*(x(1)+10*x(2))+4*(x(2)-2*x(3))^3
10*(x(3)-x(4))-8*(x(2)-2*x(3))^3
-10*(x(3)-x(4))-40*(x(1)-x(4))^3];
然后在命令窗口输入:X0=[1 2 3 4]’,再输入:fast(@func,gfunc,X0);即可(加粗部分,X0为初始点,任意),运行结果如下:
(a)精度较高时的情况 (b)精度较低时的情况
图1-2-1 最速下降法运行结果
由于最速下降法收敛速度很缓慢,要达到较高精度,迭代的次数要很大,正如上图(a)所示,当设置的精度较高时(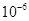
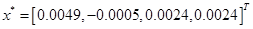
2.4 体会
Matlab的运算速度不太令人满意,当然有时程序的运算速度是和算法及编程实现者的水平密不可分的!
在最速下降法的实现过程中,刚开始使用subs函数计算函数值和一般的函数调用方式会大大降低程序的速度,几经修改后,得到了上面的程序,原来的程序迭代5000次需要30分钟不只,改进后的程序仅需不到10秒的时间,即使是要达到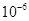
这其中,应用了函数句柄和匿名函数,其实它们就是为了使 feval 及借助于它的泛函指令工作更可靠;使“函数调用”像“变量调用”一样方便灵活;提高函数调用速度,特别在反复调用情况下更显效率;提高软件重用性,扩大子函数和私用函数的可调用范围;迅速获得同名重载函数的位置、类型信息.
函数句柄和匿名函数的操作符均为@,匿名函数是函数句柄的一种特殊用法,这里所得到的函数句柄变量不指向特定的函数(即不指向函数M文件中的函数名),而是指向一个函数表达式(具体表达式).在命令窗口中输入@func就是用了函数句柄将其传给objf变量,而step=golden(@(x)objf(X0+x*d),0,1,epsilon);则是通过匿名函数将函数传给golden程序,此两处的改变就大大提高了程序的运行速度!
3. 牛顿法
牛顿法也是一种经典的无约束优化方法,并且其收敛速度快,具有自适应的特点,至今仍受到人们的青睐.
3.1 思想
牛顿法的基本思想是用迭代点处的一阶导数(梯度)和二阶导数(Hesse阵)对目标函数进行二次函数近似,然后把二次模型的极小点作为新的迭代点,并不断重复这一过程,直至达到精度.
3.2 算法
牛顿法的算法如下:
Step2 计算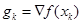
3.3 实现及结果
采用matlab 2011a实现,具体程序见附录Newton.m文件.
下面以上机题第一题为例介绍具体使用方法:
上机题1的优化目标函数为
仍然使用最速下降法中建立的func.m文件,在命令窗口中输入(加粗部分):X0=[1 2 3 4]’;Newton(@func,X0);即可按默认的精度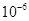
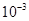
(a)采用默认精度 (b)精度为0.001
图1-3-1 牛顿法运行结果
牛顿法收敛速度快,正如上图(a)所示,达到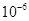
3.4 体会
由于牛顿法收敛速度快,且人工求目标函数的梯度、Hesse矩阵,有时较为繁杂,故算法实现时,实现了自动求梯度和Hesse矩阵,这样便在程序的易用性和时间复杂度两者间得到了很好的折中.
第二篇 约束优化
求解约束优化问题的经典算法是罚函数法,其基本思想是:根据约束条件的特点将其转化为某种惩罚函数加到目标函数中去,从而将约束优化问题转化为一系列的无约束优化问题来求解。
1. 外点法
外点法适合求解如下约束优化问题:
但本次实验仅需求解如下约束优化问题:
而且,等式约束也可以转化为不等式约束!
1.1 思想方法
构造罚函数
和增广目标函数
其中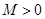
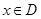
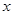
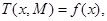
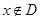
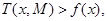
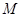
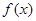
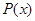
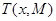
1.2 算法
外点法的算法如下:
1.3 实现及结果
采用matlab 2011a实现,无约束优化采用牛顿法,即直接调用第一篇中的Newton函数,具体程序见附录EPM.m文件.
程序中的Min=Newton(@augf,Xk,epsilon);是无约束优化函数的调用,参数augf为增广目标函数文件名,故还需建立该文件,详见附录augf.m文件.
augf.m中还涉及到(调用)了两个函数:func.m和constrains.m,前者为目标函数文件,与前面的func.m一样,只是目标函数不同而已,后者为约束函数,详见附录constrains.m文件.
现举两个例子,来说明程序运行方法及运行结果.
例1求解以下约束优化问题
建立func.m文件和constrains.m文件如下:
func.m文件
function f = func( x )
f=(1/3)*(x(1)+1)^3+x(2);
end
constrains.m文件
function g= constrains( x )
g(1)=x(1)-1;%约束1
g(2)=x(2);%约束2
end
然后修改augf.m文件中不等式约束的个数变量inequN=2、去掉外点法罚函数部分的注释并注释掉内点法对应部分(augf.m文件中有详细说明);保存后在命令窗口输入(粗体部分):EPM([-1 -1]');或EPM([-1 -1]',10,2);运行结果分别如下图(a)、(b)所示:
(a)采用默认值的结果 (b)M=10,r=2时的结果
图2-1-1 例1外点法运行结果
本例的实际最优解就是[1,0],可见程序运行正确,由上图可知增大M和r的初值可加快收敛速度.
例2求解以下约束优化问题
建立func.m文件和constrains.m文件如下:
func.m文件
function f = func( x )
f=x(1)^3+x(2)^2;
end
constrains.m文件
function g= constrains( x )
g=x(1)+x(2)-1;
end
然后修改augf.m文件中不等式约束的个数变量inequN=1、去掉外点法罚函数部分的注释并注释掉内点法对应部分(augf.m文件中有详细说明);保存后在命令窗口输入(粗体部分):EPM([2 -2]');或EPM([2 -2]',10,2);运行结果分别如下图(a)、(b)所示:
(a)采用默认值的结果 (b)M=10,r=2时的结果
图2-1-2 例2外点法运行结果
本例没有实际最优解,但有局部最优解,可见程序运行正确,由上图可知增大M和r的初值可加快收敛速度.
2. 内点法
内点法一般只适用于求解如下约束优化问题:
2.1 思想
内点法也属于罚方法的范畴,其基本思想是保持每一个迭代点![]() 是可行域D内的点,可行域的边界被筑起一道很高的“围墙”作为障碍,当迭代点靠近边界时,增广目标函数的值骤然增大,以示“惩罚”,并阻止迭代点穿过边界.因此内点法也成为内罚函数法或障碍函数法.
是可行域D内的点,可行域的边界被筑起一道很高的“围墙”作为障碍,当迭代点靠近边界时,增广目标函数的值骤然增大,以示“惩罚”,并阻止迭代点穿过边界.因此内点法也成为内罚函数法或障碍函数法.
2.2 算法
内点法的算法如下:
2.3 结果
采用matlab 2011a实现,无约束优化采用牛顿法,即直接调用第一篇中的Newton函数,具体程序见附录IPM.m文件.
程序中用到的augf.m文件、func.m文件、constrains.m文件与外点法用到的为同一文件,使用时只需注释掉另外一部分并取消内点法部分的注释即可.
仍以外点法中的两个例子为例,来说明程序运行方法及运行结果.
只需修改augf.m文件中不等式约束的个数变量inequN=2、去掉内点法罚函数部分的注释并注释掉外点法对应部分(augf.m文件中有详细说明);保存
对于例1,在命令窗口输入(粗体部分):IPM([2 2]');或IPM([2 2]',20,0.5);运行结果分别如下图(a)、(b)所示:
(a)采用默认值的结果 (b)M=20,c=0.5时的结果
图2-2-1 例1外点法运行结果
本例的实际最优解就是[1,0],可见程序运行正确,由上图可知增大M和c的初值可加快收敛速度.
对于例2,在命令窗口输入(粗体部分):IPM([1 2]');或IPM([1 2]',20,0.3);运行结果分别如下图(a)、(b)所示:
(a)采用默认值的结果 (b)M=20,c=0.3时的结果
图2-2-2 例2外点法运行结果
本例没有实际最优解,但有局部最优解,可见程序运行正确,由上图可知增大M和c的初值可加快收敛速度.
附录 源程序清单
1. func.m文件:
function f = func( x )
%--------目标函数------
% ------liuzhi------
%------2012/11/12------
% 输出:目标函数表达式
% 提示:注释:Ctrl + R 取消注释:Ctrl + T
% 提示:注释(取消注释)一行,请将光标置于该行任意位置,使用上述快捷键
% 提示:注释(取消注释)多行,请选中多行(不需全选),使用上述快捷键
% 提示:注意保存!!!
% ----以下为 无约束优化 部分的目标函数----
% ---------------黄金分割法用------------
% f=x(1)^2-x(1)+6;
% ---------------最速下降法、牛顿法用------------
% f=(x(1)+10*x(2))^2+5*(x(3)-x(4))^2+(x(2)-2*x(3))^4+10*(x(1)-x(4))^4;
% ----以下为 约束优化 部分的目标函数----
% ----对应 约束函数 见 constrains.m 文件----
f=(1/3)*(x(1)+1)^3+x(2);
% f=2*x(1)+3*x(2);
% f=x(1)^3+x(2)^2;
end
2. gfunc.m文件:
function gf = gfunc( x )
%目标函数的梯度
% ------liuzhi------
%------2012/11/12------
%输出:目标函数的梯度表达式
gf=[2*(x(1)+10*x(2))+40*(x(1)-x(4))^3
20*(x(1)+10*x(2))+4*(x(2)-2*x(3))^3
10*(x(3)-x(4))-8*(x(2)-2*x(3))^3
-10*(x(3)-x(4))-40*(x(1)-x(4))^3];
end
3. constrains.m文件:
function g= constrains( x )
%------------约束函数--------------
% 不等式约束,也很容易加入等式约束
% 提示:注释:Ctrl + R 取消注释:Ctrl + T
% 提示:注释(取消注释)一行,请将光标置于该行任意位置,使用上述快捷键
% 提示:注释(取消注释)多行,请选中多行(不需全选),使用上述快捷键
% 提示:注意保存!!!
%---对应目标函数 f=(1/3)*(x(1)+1)^3+x(2) 的不等式约束---
g(1)=x(1)-1;%约束1
g(2)=x(2);%约束2
%---对应目标函数 f=2*x(1)+3*x(2); 的不等式约束---
% g=1-2*x(1)^2-x(2)^2;
%---对应目标函数 f=x(1)^3+x(2)^2; 的不等式约束---
% g=x(1)+x(2)-1;
end
4. augf.m文件:
function af = augf( x )
%-----增广目标函数--------
% ------liuzhi------
%------2012/12/12--------
% 此函数用来得到增广目标函数
% 使用 外点法 时,请注释掉 内点法 部分
% 使用 内点法 时,请注释掉 外点法 部分
% 提示:注释:Ctrl + R 取消注释:Ctrl + T
% 提示:注释(取消注释)一行,请将光标置于该行任意位置,使用上述快捷键
% 提示:注释(取消注释)多行,请选中多行(不需全选),使用上述快捷键
% 提示:注意保存!!!注意修改 inequN 的值!!!
global M inequN penf; %penalty function %注意修改 inequN 的值!!!
% M:惩罚(/障碍)因子;inequN:不等式约束个数;penf:罚(/障碍)函数
inequN=2; %注意修改 inequN 的值!!!
penf=0;
g=constrains(x);%不等式约束
%---------以下为外点罚函数------------
% global Xk;
% G=constrains(Xk);%计算各约束条件在 Xk 处的值,以便得到罚函数
% for i=1:inequN
% if(G(i)<0)
% penf=penf+g(i)*g(i);
% end
% end
%---------以下为内点障碍函数------------
for i=1:inequN
%penf=penf-log(g(i));
penf=penf+1/g(i);
end
%---------以下为增广目标函数------------
af=func(x)+M*penf;
end
5. golden.m文件:
function [min,fmin,k,G,dx] = golden(objf,a,b,epsilon)
%---------------------黄金分割法(一维)------------------------
% --------liuzhi---------
%----------------------2012/11/12-----------------------------
%-------------------------------------------------------------
%
%@@@ function:[min,fmin,k,I,dx] = golden(objf,a,b,epsilon) @@@
%
%输入:objf:目标函数(一维),a,b是搜索区间端点,
% epsilon:精度(默认为:10^-6).
%输出:min:极小点,fmin:极小点对应函数值,
% k:迭代次数,I:迭代区间,dx:.
%--------------------------------------------------------------
%
%使用方法:
% 1.先建立名为func的.m文件,在里面写入表达式,举例如下:
% function f = func( x )
% f=x(1)^2-x(1)+6;
% end
% 2.在命令窗口中
% (1)输入:
% golden(@func,0,1,0.0001);
% 程序自动输出所有输出参数;
% (2)输入:
% golden(@func,0,1);
% 程序按照默认的epsilon计算,并自动输出所有输出参数;
% (3)
% 如果输入的命令中输出参数不为0,则按照从左至右的顺序输
% 出n个参数,但命令结尾不能加‘;’号.
% 如输入:min=golden(@func,0,1),则输出:
% Not enough input arguments!
% Use default: epsilon=10^-6 !
%min =
% 0.5000
%--------------------------------------------------------------
% function [min,fmin,k,G,dx] = golden(objf,a,b,epsilon)
if nargin==3
epsilon = 0.000001;
disp(' Not enough input arguments!');
disp(' Use default: epsilon=10^-6 !');
elseif nargin<3
error(' Not enough input arguments!');
end
x1=a+0.382*(b-a);
x2=a+0.618*(b-a);
objf1=objf(x1);
objf2=objf(x2);
k=1; I(k,:)=[a,x1,x2,b];
while abs(b-a)>epsilon
if objf1>objf2 %在[x1,b]
a=x1; x1=x2;
objf1=objf2;
x2=a+0.618*(b-a);
objf2=objf(x2);
else %在[a,x2]
b=x2; x2=x1;
objf2=objf1;
x1=a+0.382*(b-a);
objf1=objf(x1);
end
k=k+1;
I(k,:)=[a,x1,x2,b];
end
dx=abs(b-a);
min=(a+b)/2;
fmin=objf(min);
if nargout==0
disp(' 极小点:');
disp(min);
disp(' 极小点对应函数值:');
disp(fmin);
disp(' 迭代次数:');
disp(k);
disp(' 迭代区间:');
disp(' a x1 x2 b');
disp(I);
disp(' 迭代终止时的区间长度:');
disp(dx);
end
end
6. fast.m文件:
%---------------------最速下降法(步长采用0.618法)--------------
% --------liuzhi---------
%------------------------2012/11/12---------------------------
%-------------------------------------------------------------
%
%@@@ function:[ Min,Fmin,k ]=golden(objf,gobjf,X0,epsilon) @@@
%
%输入:objf:目标函数; gobjf:目标函数的梯度函数,
% X0:搜索起始点; epsilon:精度(默认为:10^-6).
%输出:Min:极小点,
% Fmin:极小点对应函数值矩阵,
% k:迭代次数.
%-------------------------------------------------------------%
%
%使用方法:
% 1.先建立名为func的.m文件,在里面写入表达式,举例如下:
% function f = func( x )
% f=100*(x(1)^2-x(2))^2+(x(1)-1)^2;
% end
% 再建立名为gfunc的.m文件,在里面写入func的梯度表达式,如下:
% function f = gfunc( x )
% gf=[400*x(1)*(x(1)^2-x(2))+2*(x(1)-1)
% -200*(x(1)^2-x(2))];
% end
% 2.在命令窗口中
% 首先输入:X0=[1,2]' 接着
% (1)输入:
% fast(@func,@gfunc,X0,0.0001);
% 程序自动输出所有输出参数,如下:
% 极小点:
% 1.0001
% 1.0002
%
% 极小点对应函数值:
% 1.1837e-008
%
% 迭代次数:
% 1452
% (2)输入:
% fast(@func,@gfunc,X0);
% 程序按照默认的epsilon计算,并自动输出所有输出参数;
% (3)
% 如果输入的命令中,输出参数不为0,则按照从左至右的顺序输
% 出n个参数,但命令结尾不能加‘;’号.
% 如输入:min=fast(@func,@gfunc,X0) 则输出:
% Not enough input arguments!
% Use default: epsilon=10^-6 !
%min =
% 1.0000
% 1.0000
%function [ Min,fmin,k ] = fast( objf,gobjf,X0,epsilon )
%--------------------------------------------------------------
function [ Min,fmin,k ] = fast( objf,gobjf,X0,epsilon )
disp(' --------最速下降法(步长采用0.618法)--------');
if nargin==3
epsilon = 0.000001;
disp(' Not enough input arguments!');
disp(' Use default: epsilon=10^-6 !');
elseif nargin<3
error(' Not enough input arguments!');
end
syms x;
k=0;maxk=50000;
d=-gobjf(X0);
while(norm(d)>epsilon)
step=golden(@(x)objf(X0+x*d),0,1,epsilon);
%d=d/norm(d);
X0=X0+step*d;
k=k+1;
d=-gobjf(X0);
end
Min=X0;
fmin=objf(X0);
if norm(d)>epsilon
disp(' 未达到精度!');
end
if nargout==0
disp(' 极小点:');
disp(Min);
disp(' 极小点对应函数值:');
disp(fmin);
disp(' 迭代次数:');
disp(k);
end
end
7. Newton.m文件:
%-----------------牛顿法------------------%
% --------liuzhi---------
%---------------2012/11/16----------------%
%-----------------------------------------%
%输入:objf:目标函数,X0:搜索起始点,
% epsilon:精度(默认为:10^-6);
%输出:Min:极小点,fmin极小点对应函数值,
% k:迭代次数
%-----------------------------------------%
function [ Min,fmin,k ] = Newton( objf,X0,epsilon )
if nargin==2
epsilon = 0.000001;
disp(' Not enough input arguments! epsilon=10^-6');
elseif nargin<2
error(' Not enough input arguments!');
end
syms x x1 x2 x3 x4 x5 x6 x7 x8;
n=length(X0);
y=[x1 x2 x3 x4 x5 x6 x7 x8];
for i=1:n
v(i)=y(i);
end
k=0;
gobjf=jacobian(objf(v),v);%求梯度
Hess=jacobian(gobjf,v);%求Hesse矩阵
G=subs(gobjf,v,X0)';
while(norm(G)>epsilon)
H=subs(Hess,v,X0);
delta=-inv(H)*G;
X0=X0+delta;
G=subs(gobjf,v,X0)';
k=k+1;
end
Min=X0;fmin=objf(X0);
if nargout==0
disp(' 极小点:');
disp(Min);
disp(' 极小点对应函数值:');
disp(fmin);
disp(' 迭代次数:');
disp(k);
end
end
8. EPM.m文件:
% -----------------外点法------------------%
% --------liuzhi---------
% ---------------2012/12/12----------------%
% -----------------------------------------%
% function [ Min,fmin,k ] = EPM( X0,M1,r,epsilon )
% 输入:X0:搜索起始点,M1:初始惩罚因子(默认为:1),
% r:惩罚因子变化的倍数(默认为:2),
% epsilon:精度(默认为:10^-6);
% 输出:Min:极小点,fmin:极小点对应函数值,
% k:迭代次数
function [ Min,fmin,k ] = EPM( X0,M1,r,epsilon )
global M inequN Xk;
% M:惩罚因子;inequN:不等式约束个数
disp(' --------外点法--------');
if nargin==3
epsilon = 0.000001;
disp(' Not enough input arguments! epsilon=10^-6');
elseif nargin<3
disp(' Use default: M1=1 !');
disp(' Use default: r=2 !');
disp(' Use default: epsilon=10^-6 !');
M1=1;r=2;epsilon = 0.000001;
elseif nargin<1
error(' Not enough input arguments!');
end
M=M1;
if M<=0
error(' M大于零!');
end
if r<=1
error(' r大于1 !');
end
k=1;
stop=0;%外点法中止条件
Xk=X0;
while(stop==0)
Min=Newton(@augf,Xk,epsilon);
Xk=Min;
g=constrains(Xk);
for i=1:inequN %外点法中止条件
if(-g(i)<=epsilon)
stop=1;
else
stop=0;break;
end
end
M=M*r;
k=k+1;
end
fmin=func(Min);
if nargout==0
disp(' 极小点:');
disp(Min);
disp(' 极小点对应函数值:');
disp(fmin);
disp(' 迭代次数:');
disp(k);
end
end
9. IPM.m文件:
% -----------------内点法------------------%
% --------liuzhi---------
% ---------------2012/12/20----------------%
% -----------------------------------------%
% function [ Min,fmin,k] = IPM( X0,M1,c,epsilon )
% 输入:X0:搜索起始点,M1:初始惩罚因子(默认为:10),
% c:惩罚因子变化的倍数(默认为:0.7),
% epsilon:精度(默认为:10^-6);
% 输出:Min:极小点,fmin极小点对应函数值,
% k:迭代次数
function [ Min,fmin,k ] = IPM( X0,M1,c,epsilon )
disp(' --------内点法--------');
if nargin==3
epsilon = 0.000001;
disp(' Not enough input arguments! epsilon=10^-6');
elseif nargin<3
disp(' Use default: M1=10 !');
disp(' Use default: c=0.7 !');
disp(' Use default: epsilon=10^-6 !');
M1=10;c=0.7;epsilon = 0.000001;
elseif nargin<1
error(' Not enough input arguments!');
end
global M penf;
% M:障碍因子;inequf:障碍函数
k=1;
M=M1;
if M<=0
error(' M大于零!');
end
if(c>=1 || c<=0)
error(' c大于0小于1 !');
end
stop=1;%内点法中止条件,初始化为:1
while(stop>epsilon)
Min=Newton(@augf,X0,epsilon );
X0=Min;
M=M*c;
k=k+1;
stop=M*penf;%内点法中止条件:障碍函数准则
end
fmin=func(Min);
if nargout==0
disp(' 极小点:');
disp(Min);
disp(' 极小点对应函数值:');
disp(fmin);
disp(' 迭代次数:');
disp(k);
end
end
对于优化问题:![clip_image171[4] clip_image171[4]](https://i-blog.csdnimg.cn/blog_migrate/ec148d05de8794a78ae9f08a6ea0cacb.jpeg) 是无最优解的,这是因为:
是无最优解的,这是因为:
那么
故此函数无最小值。
很显然上式的值很小,计算器求得:-5828756399,








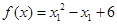
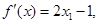
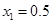
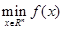
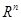
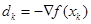
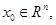
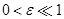

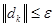
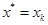
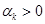
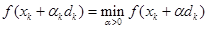
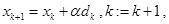
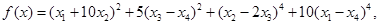

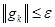
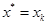
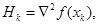
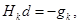
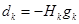

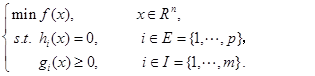
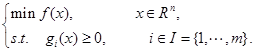
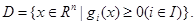
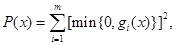
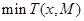
![clip_image126[4] clip_image126[4]](https://i-blog.csdnimg.cn/blog_migrate/27f98513fe94dcf75423c5cc98ed88f8.jpeg)
![clip_image129[4] clip_image129[4]](https://i-blog.csdnimg.cn/blog_migrate/8cc77f9e814f1ae87bbb13e423ed8075.jpeg)
![clip_image131[4] clip_image131[4]](https://i-blog.csdnimg.cn/blog_migrate/6042cca13cb30206ee9c17e4b39862de.jpeg)
![clip_image134[4] clip_image134[4]](https://i-blog.csdnimg.cn/blog_migrate/f6caa7f1d1975936ff1d87a7009b8923.jpeg)
![clip_image084[7] clip_image084[7]](https://i-blog.csdnimg.cn/blog_migrate/eefb015282f3bed4611802e69a82a831.jpeg)
![clip_image166[4] clip_image166[4]](https://i-blog.csdnimg.cn/blog_migrate/df11961c214dfaee79fc5581fc13a13d.jpeg)
![clip_image169[4] clip_image169[4]](https://i-blog.csdnimg.cn/blog_migrate/7ef56fef3320ced4296b733d1ad1a11f.jpeg)
![clip_image181[4] clip_image181[4]](https://i-blog.csdnimg.cn/blog_migrate/76e0747c375a5f6575a6feed5133cfc9.jpeg)
![clip_image193[4] clip_image193[4]](https://i-blog.csdnimg.cn/blog_migrate/023404dc94a9217af13deee37728a92c.jpeg)
![clip_image195[4] clip_image195[4]](https://i-blog.csdnimg.cn/blog_migrate/8a33709005d442573058fd63a64f86c9.jpeg)














 2089
2089

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








