条件数表征函数相对于输入的微小变化而变化的快慢程度。输入被轻微扰动而迅速改变的函数对于科学计算来说可能是有问题的,因为输入中的舍入误差可能导致输出的巨大变化。
大多数深度学习算法都涉及某种形式的优化。优化指的是改变x以最小化或最大化某个函数f(x)的任务。我们通常以最小化f(x)指代大多数最优化问题。最大化可经由最小化算法最小化-f(x)来实现。
我们把要最小化或最大化的函数称为目标函数(objective function)或准则(criterion)。当我们对其进行最小化时,我们也把它称为代价函数(cost function)、损失函数(loss function)或误差函数(error function)。梯度下降法的核心,是最小化目标函数。
导数f’(x)代表f(x)在点x处的斜率。换句话说,它表明如何缩放输入的小变化才能在输出获得相应的变化:f(x+ε)≈f(x)+εf’(x)。因此导数对于最小化一个函数很有用,因为它告诉我们如何更改x来略微地改善y。例如,我们知道对于最够小的ε来说,f(x-εsign(f’(x)))是比f(x)小的。因此我们可以将x往导数的反方向移动一小步来减少f(x)。这种技术被称为梯度下降(gradient descent)。
当f’(x)=0,导数无法提供往哪个方向移动的信息。f’(x)=0的点称为临界点(critical point)或驻点(stationary point)。一个局部极小点(local minimum)意味着这个点的f(x)小于所有邻近点,因此不可能通过移动无穷小的步长来减少f(x)。一个局部极大点(local maximum)意味着这个点的f(x)大于所有邻近点,因此不可能通过移动无穷小的步长来增大f(x).有些临界点既不是最小点也不是最大点。这些点被称为鞍点(saddle point)。
临界点是斜率为零的点。这样的点可以是局部极小点(local minimum),其值低于相邻点;局部极大点(local maximum),其值高于相邻点;或鞍点,同时存在更高和更低的相邻点。
使f(x)取得绝对的最小值(相对所有其他值)的点是全局最小点(global minimum)。函数可能只有一个全局最小点或存在多个全局最小点,还可能存在不是全局最优的局部极小点。在深度学习的背景下,我们要优化的函数可能含有许多不是最优的局部极小点,或者还有很多处于非常平坦的区域内的鞍点。尤其是当输入是多维的时候,所有这些都将使优化变得困难。因此,我们通常寻找使f非常小的点,但这在任何形式意义下并不一定是最小。
当存在多个局部极小点或平坦区域时,优化算法可能无法找到全局最小点。在深度学习的背景下,即使找到的解不是真正最小的,但只要它们对应于代价函数显著低的值,我们通常就能接受这样的解。
针对具有多维输入的函数,我们需要用到偏导数(partial derivative, 在数学中,一个多变量的函数的偏导数是它关于其中一个变量的导数,而保持其它变量恒定(相对于全导数,在其中所有变量都允许变化)。函数f关于变量x的偏导数写为f’x或 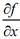
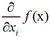
在u(单位向量)方向的方向导数(directional derivative)是函数f在u方向的斜率。换句话说,方向导数是函数f(x+αu)关于α的导数(在α=0时取得)。使用链式法则,我们可以看到当α=0时, 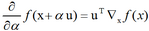
其中θ是u与梯度的夹角。将‖u‖2=1代入,并忽略与u无关的项,就能简化得到 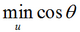
最速下降建议新的点为x’=x-ε▽xf(x)。其中ε为学习率(learning rate),是一个确定步长大小的正标量。我们可以通过几种不同的方式选择ε。普遍的方式是选择一个小常数。有时我们通过计算,选择使方向导数消失的步长。还有一种方法是根据几个ε计算f(x-ε▽xf(x)),并选择其中能产生最小目标函数值的ε。这种策略被称为线搜索。
最速下降在梯度的每一个元素为零时收敛(或在实践中,很接近零时)。在某些情况下,我们也许能够避免运行该迭代算法,并通过解方程▽xf(x)=0直接跳到临界点。
虽然梯度下降被限制在连续空间中的优化问题,但不断向更好的情况移动一小步(即近似最佳的小移动)的一般概念可以推广到离散空间。递增带有离散参数的目标函数被称为爬山(hill climbing)算法。
梯度下降法(Gradient descent):是一个一阶最优化算法,通常也称为最速下降法。要使用梯度下降法找到一个函数的局部极小值,必须向函数上当前点对应梯度(或者是近似梯度)的反方向的规定步长距离点进行迭代搜索。如果相反地向梯度正方向迭代进行搜索,则会接近函数的局部极大值点,这个过程则称为梯度上升法。
梯度下降方法基于以下的观察:如果实值函数F(x)在点a处可微(导数)且有定义,那么函数F(x)在a点沿着梯度(在单变量的实值函数的情况,梯度只是导数,或者,对于一个线性函数,也就是线的斜率。梯度一词有时用于斜度,也就是一个曲面沿着给定方向的倾斜程度。)相反的方向-▽F(a)下降最快。
梯度下降法的缺点包括:(1)、靠近极小值时速度减慢;(2)、直线搜索可能会产生一些问题;(3)、可能会”之字型”地下降。
批量梯度下降法(Batch Gradient Descent, BGD):是梯度下降法最原始的形式,它的具体思路是在更新每一参数时都使用所有的样本来进行更新。优点:全局最优解,易于并行实现;缺点:当样本数目很多时,训练过程会很慢。
随机梯度下降法(Stochastic Gradient Descent, SGD):由于批量梯度下降法在更新每一个参数时,都需要所有的训练样本,所以训练过程会随着样本数量的加大而变得异常的缓慢。随机梯度下降法正是为了解决批量梯度下降法这一弊端而提出的。随机梯度下降是通过每个样本来迭代更新一次。SGD伴随的一个问题时噪音较BGD要多,使得SGD并不是每次迭代都向着整体最优化方向。优点:训练速度快;缺点:准确度下降,并不是全局最优,不易于并行实现。
小批量梯度下降法(Mini-batch Gradient Descent, MBGD):MBGD在每次更新参数时使用b个样本。
BGD在每次迭代时使用全部样本;SGD在每次迭代时使用1个样本;MBGD在每次迭代时使用b个样本。
梯度下降优化算法包括:Momentum、NAG、Adagrad、RMSprop、Adam等。
待后面介绍线性回归时会给出梯度下降法的C++实现。










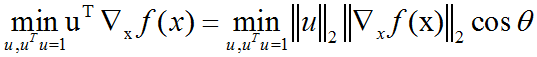














 320
320











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








