计算快速汉明距离

汉明距离，作为一种衡量特征距离的计算方法，在很多场合都有应用，其主要思想是找到两个特征之间的差异大小，也可以说是相似性。

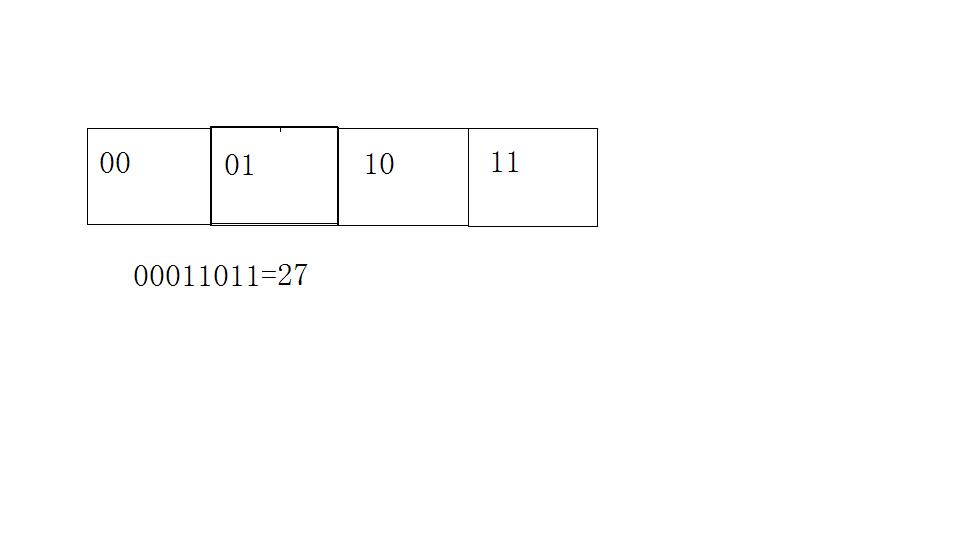
我是在图像处理中用到的，项目中需要计算图像梯度方向，我选择了四个方向，这样就可以用二位二进制表示，分别为 0,1,2,3，也就是 00,01,10,11，这四种情况。这样，我就可以可以把，例如四个临近点，对应梯度特征合并为一个特征向量，如图

只需要一个字节的大小空间就可以表示一个特征。那么，我来用这个特征描述两张图， 假设A，B，就得到了两个特征，featureA，featureB，在假设图像大小为100*100的8bit灰度图像，选择水平方向的四个像素，那么我就可以得到 100*25个单字节的描述特征。接下来，我要怎么衡量这两张图是不是相似，就要用到汉明距离（其他距离也可以，这里直说汉明距离）。如果两个图像在这种特征下是相似的，那意味着他们特征的对应比特位应该是尽可能多的一致，也就是说，featureA ^ featureB ，特征的异或结果中1 的个数尽可能的少。这就涉及到，我们如何计算1的个数。这在leetcode和剑指offer等书中都有类似笔试面试题。

常规解法就是移位判断是不是1，是则计数，需要注意，应该要判断给定数（这里用tmp表示）的符号，否则可能死循环。

int CountOne(int tmp)
{
int count=0;
if(0==tmp)
return count;
else if(tmp>0)
{
    while(tmp)
  {
  if(tmp&1)
    ++count;
  tmp=tmp>>1;
  }
}
else
{
tmp=-tmp;
count=1;
while(tmp)
  {
  if(tmp&1)
    ++count;
  tmp=tmp>>1;
  }
}
return count;
}

这样还是不方便，我们可以不对tmp移位：

int CountOneVersion2(int tmp)
{
int flag=1;
int count=0;
while(flag)
{
if(flag&tmp)
++count;
flag=flag<<1;
}
return count;
}

这样就少去了判断符号的麻烦。

还有一种解法，那就是考虑到tmp每次减一后，最后一位1都会发生变化，这样我们把剩下的保留，下次再减一，知道tmp为零位置，这样就可以知道其中1的个数。

int CountOneVersion3(int n)
{
int count=0;
while(n)
{
++count;
n=n&(n-1);
}
return count;
}

以上是采用移位的方法，我们还可以不用移位，那就是下面的快速汉明距离计算的问题。我们先取三个数，这里考虑unsigned char 型，也就一个字节的情况。分别是 AA=85,即01010101，BB=51，即00110011，CC=15，即00001111；主要思想就是计算1的和，(1)一行是计算相邻两个位置的和，得到的结果最多需要两位，然后(2)一行在计算相邻四个位置的和，计算结果最多需要四位.(3)一行再把高四位和低四位相加，得到的就是1的个数。

unsigned char A,B,Ch,D;
const unsigned char AA = 85;
const unsigned char BB = 51;
const unsigned char CC = 15;

  A = tmp; B = A&AA; Ch = (A>>1)&AA;//(1)
  D = B+Ch; B = D &BB; Ch = (D>>2)&BB;//(2)
  D = B+Ch; B = D & CC; Ch = (D>>4)&CC;//(3)
ss += B+Ch;

应为是在硬件上实现，所以每个时钟周期都要计较，要做性能优化，通过这样的位运算，能够显著提升速度，这种计算单元重复度相当高，所以性能会提升很多。

今天突然想到了，就总结一下，不自己写出来，永远记不住，记不清。

有不当之处，请指正！