动态树-LCT-bzoj2002弹飞绵羊

我的第一篇博客给LCT（Link-Cut Tree）^_

动态树要求我们维护一个由若干棵子结点无序的有根树组成的森林。 要求这个数据结构支持对树的分割，合并，对某个点到它的根的路径的某些操作, 以及对某个点的子树进行的某些操作。其中解决问题使用最多的是LCT，这里就主要介绍一下LCT吧。

其实动态树主题思想跟树链剖分差不多，非常频繁的使用了Splay。

类似树链剖分的定义：
PreferredChild：如果结点v的子树中, 最后被访问的结点在子树w中, 这里w是v的儿子, 那么就称w是v的PreferredChild
PreferredEdge：每个点到它的PreferredChild的边称作PreferredEdge
PreferredPath：由PreferredEdge连接成的不可再延伸的路径称为 PreferredPath

一颗LCT
容易得出整棵树就被划分成了若干条 PreferredPath。对每条 PreferredPath， 用这条路上的点的深度作为关键字, 用一棵平衡树来维护它（一般使用Splay，理论上Treap也可以，可是我从没有看见有人这样做过）。然后这棵平衡树就被叫做AuxiliaryTree。我们把AuciliaryTree中深度最小的节点的父亲节点称为PathParent。

Link-Cut Trees 就是将要维护的森林中的每棵树 T 表示为若干个 AuxiliaryTree， 并通过PathParent将这些AuxiliaryTree连接起来的数据结构

图解
^

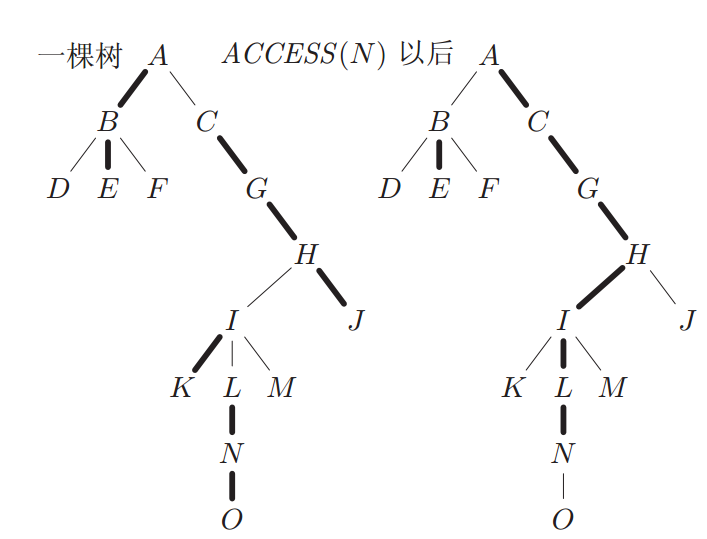
基本操作
首先是它最基本的操作 access(x)。
一旦我们调用access(x)，那么从点x到根结点的路径就成为一条新的 PreferredPath。 如果路径上的某个节点u不是它的父亲v的PreferredChild， 那么我们要将v的PreferredChild变为u ， 原本包含v的PreferredPath/AuxiliaryTree将不再包含节点v及其之上的部分。

其他操作
-find_root(x)操作-即找到节点x所在树的根节点。
先access(x)，然后将x Splay到所在AuxiliaryTree的根节点。找到这棵AuxiliaryTree最左端的点即可。

-cut(x)操作-即断开x与其父亲节点的边。
先access(x)，然后将x Splay到所在AuxiliaryTree的根节点。断开x和父亲节点的边。

-link(v,w)操作-让v成为w的新的儿子。其中v是一棵树的根结点，并且v和w是不同的两棵树中的结点。
先访问v，然后修改v所属的AuxiliaryTree的PathParent为w，然后再次访问v。

下面是LCT的一道例题 bzoj2002弹飞绵羊
题目大意 ：n个装置编号为0-n-1，每个装置一个值表示一旦到这个装置上就会往后弹的步数，要求最少跳多少步能从输入的第x号节点弹出去。

做法 ：若可以从i弹到j则连一条从j到i的边，若弹飞了，则连一条从0到i的边。

#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
using namespace std;
const int maxn=200010;
int fa[maxn],size[maxn],ch[maxn][2];
int n;
void maintain(int x){
    size[x]=size[ch[x][0]]+size[ch[x][1]]+1;
}
bool isroot(int x){
    return ch[fa[x]][0]!=x && ch[fa[x]][1]!=x;
}
void rotate(int x){
    int y=fa[x],z=fa[y];
    int l,r;
    if(ch[y][0]==x) l=0;
    else l=1;
    r=l^1;
    if(!isroot(y)){
        if(ch[z][0]==y) ch[z][0]=x;
        else ch[z][1]=x;
    }
    fa[x]=z;
    fa[y]=x;
    fa[ch[x][r]]=y;
    ch[y][l]=ch[x][r];
    ch[x][r]=y;
    maintain(y);
}
void splay(int x){
    while(!isroot(x)){
        int y=fa[x],z=fa[y];
        if(!isroot(y)){
            if(x==ch[y][0] ^ y==ch[z][0]) rotate(x);
            else rotate(y);
        }
        rotate(x);
    }
    maintain(x);
}
void access(int x){
    int t=0;
    while(x){
        splay(x);
        ch[x][1]=t;
        maintain(x);
        t=x;
        x=fa[x];
    }
}
void cut(int x){
    access(x);
    splay(x);
    ch[x][0]=fa[ch[x][0]]=0;
}
void link(int x,int y){
    cut(x);
    fa[x]=y;
    maintain(x);
}
int main(){
    int i,x,y,tmp;
    scanf("%d",&n);
    for(i=1;i<=n;i++){
        scanf("%d",&tmp);
        fa[i]=i+tmp>n?0:i+tmp;
        size[i]=1;
    }
    int q;
    scanf("%d",&q);
    for(i=1;i<=q;i++){
        scanf("%d%d",&x,&y);
        y++;
        if(x==1){
            access(y);
            splay(y);
            printf("%d\n",size[ch[y][0]]+1);
        }else{
            scanf("%d",&x);
            link(y,y+x>n?0:y+x);
        }
    }
    return 0;
}

^_^