logistic 函数（logistic function）

今天看SVM（支持向量机），开始先引入了logistic函数，虽然给出了一公式，但好奇logistic函数啥东东啊，为啥叫logistic呢，搜索ing。

       说简单些，logistic函数其实就是这样一个函数：

                                                                                       

非常简单吧，这个函数的曲线如下所示：

                                                                           

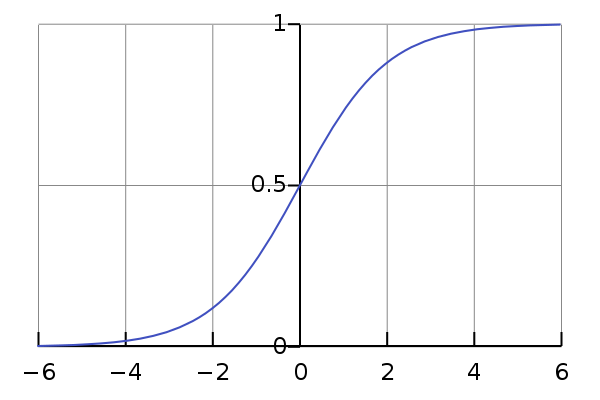
很像一个“S”型吧，所以又叫 sigmoid曲线（S型曲线）。

%%%%%%%%%%%%%%%%一下为进一步了解，普通工科学生会用就行了%%%%%%%%%%%%%%%%%%%%%

上面只是作为一般使用时了解的即可，但实际上这个函数可是大有来头：

        逻辑斯谛方程即微分方程：

                                  。

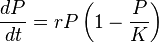         当一个物种迁入到一个新生态系统中后，其数量会发生变化。假设该物种的起始数量小于环境的最大容纳量，则数量会增长。该物种在此生态系统中有天敌、食物、空间等资源也不足（非理想环境），则增长函数满足逻辑斯谛方程，图像呈S形，此方程是描述在资源有限的条件下种群增长规律的一个最佳数学模型。在以下内容中将具体介绍逻辑斯谛方程的原理、生态学意义及其应用。

        这还要追溯到1838年，一个比利时的数学家叫Pierre-François Verhulst（1804-1849）的人，他那个时候研究人口增长的课题，提出了人口增长不但和现有人口相关，还和可用资源有关，即有一个人口的承载量，首先将营养关系反映到种群数学模型方面，是它首先导出了后来被广泛称为逻辑斯谛的方程，最初发表的时候叫Verhulst方程。但在当时并没有引起大家的注意，直到1920年两位美国人口学家Pearl和Reed在研究美国人口问题时，再次提出这个方程，才开始流行，故现在文献中通常称之为Verhulst-Pearl阻碍方程。其所以又称为逻辑斯谛方程是因为其有某种逻辑推理的含义。按现在的用语来说，它是一个说理模型，实际上是反映营养对种群增长的一种线性限制关系的说理模型。

1963年，洛伦兹发现确定性系统的随机性为，并且发现了这种随机行为对初值的敏感性。1975年，美籍华人学者李天岩和数学家约克发表“周期中蕴含着混沌”的著名文章，揭示从有序到混沌的演化过程。这些内容都包含在逻辑斯谛差分方程中。1976年R.梅在英国《自然》杂志上发表了研究逻辑斯谛方程的成果—《表现非常复杂的动力学的简单数学模型》，引起学术界极大关注，内容已远远超越了生态学领域，揭示出逻辑斯谛方程深处蕴藏的丰富内涵。

将上面的方程解出来（这个学过高等数学的人都会吧，很简单的），可以得到：

其中为初始值，很眼熟吧，变变形，是不是就类似开头提出的logistic函数了，唯一不同的事系数有所变化。

 

更多具体的内容大家可以参考维基百科：http://en.wikipedia.org/wiki/Logistic_function

或者百度搜索关键词“逻辑斯谛方程”，成堆的结果就出来了