算法分析:
螺旋矩阵用二维数组表示,坐标(x,y),即(x轴坐标,y轴坐标)
顺时针螺旋的方向是->右,下,左,上,用数值表示即是x加1格(1,0),y加1格(0,1),x减1格(-1,0),y减1格(0,-1)
坐标从(0,0)开始行走,当超出范围或遇到障碍时切换方向
螺旋矩阵用二维数组表示,坐标(x,y),即(x轴坐标,y轴坐标)
顺时针螺旋的方向是->右,下,左,上,用数值表示即是x加1格(1,0),y加1格(0,1),x减1格(-1,0),y减1格(0,-1)
坐标从(0,0)开始行走,当超出范围或遇到障碍时切换方向
经过上面的分析,思路很清晰了,千言不如一码。
import itertools
def spiral(n,m):
_status = itertools.cycle(['right','down','left','up'])#用于状态周期性的切换
_movemap = {
'right':(1,0),
'down':(0,1),
'left':(-1,0),
'up':(0,-1),
}
pos2no = dict.fromkeys([(x,y) for x in range(n) for y in range(m)])
_pos = (0,0)
_st = next(_status)
for i in range(1,n*m+1):
_oldpos = _pos
_pos = tuple(map(sum,zip(_pos,_movemap[_st])))#根据状态进行移动
if (_pos not in pos2no) or (pos2no[_pos]):#当超出范围或遇到障碍时切换方向
_st = next(_status)
_pos = tuple(map(sum,zip(_oldpos,_movemap[_st])))
pos2no[_oldpos] = i
return pos2no
def display_spiral(n,m):
pos2no = spiral(n,m)
for i in range(m):
for j in range(n):
print pos2no[(j,i)],'\t',
print '\n'
print '-'*30
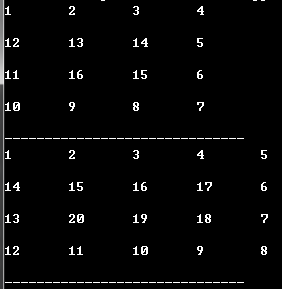
display_spiral(4,4)
display_spiral(5,4)









 本文介绍了一种使用Python实现螺旋矩阵的算法。通过定义状态切换和移动映射来控制矩阵元素的填充顺序,确保了矩阵元素按照顺时针螺旋的方式递增。文章提供了完整的代码示例并展示了如何显示生成的螺旋矩阵。
本文介绍了一种使用Python实现螺旋矩阵的算法。通过定义状态切换和移动映射来控制矩阵元素的填充顺序,确保了矩阵元素按照顺时针螺旋的方式递增。文章提供了完整的代码示例并展示了如何显示生成的螺旋矩阵。
















 1736
1736

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








