线性回归
原文地址:http://blog.csdn.net/hjimce/article/details/45418645
作者:hjimce
假设对于输入数据X(x1,x2……xn),输出数据y,对于线性回归我的简单理解就是线性拟合。因为为之前就对拟合这个词比较熟悉,对于最小二乘也是比较熟悉的。对于输入数据X,输出数据y,线性回归的基础公式为:
其中x1,x2……xn表示的是数据X的特征,而x0=1是固定的。我们希望根据已经给定的m个数据集data,求解出未知的参数,θ0,、θ1、θ2…。其实求解这个公式最简单的办法就是最小二乘。根据已给定的m个数据,我们可以列出m个方程组:
公式简化为:
如果m=n那么方程组刚好有唯一的解,如果m>n那么就要用最小二乘的公式求解超静定方程组了。以上的公式可以叫做均匀权的线性回归公式,因为每个数据点构造的方程组的权重都一样,如果每个数据点的权重不一样,那么就叫做加权的线性回归了,此时公式演化为:
这里重点讲解如何用梯度下降法求解,因为梯度下降法可以说是机器学习算法中的基础,学好梯度下降法,后面神经网络、逻辑回归这些就变得相对简单了。
现在先开始推导梯度下降法。定义代价函数为:
其中:
这里需要说明的是上标表示数据点的号码,下表表示参数的编号。
我们希望代价函数J(θ)最小化,即:
而求解这个函数的极小值,就需要对函数J(θ)求偏导,然后令个个偏导方程为0:
其中:
然后联立这n个方程组,求解可得个个参数,其实最后联立出来求解结果,就是最小二乘的求解方法了。梯度下降法与最小二乘的求解方法不一样,梯度下降法是一个迭代公式:
其中公式中的符号“:”表示迭代更新的意思。
因此梯度下降法最后求解公式为:
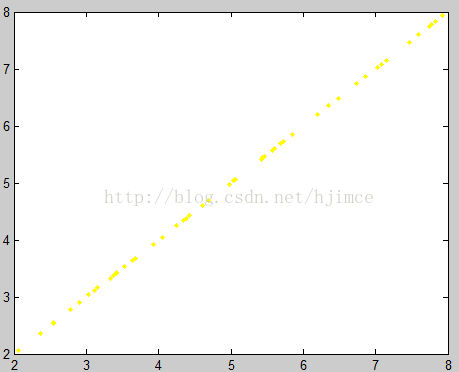
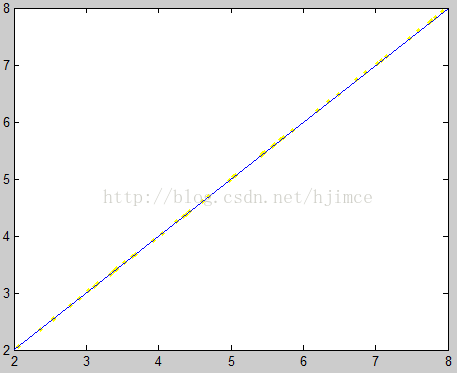
接着根据公式进行求解,matlab的代码如下:
原数据 拟合结果
*********原创文章,版权所有,转载请注明原文地址******************








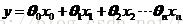
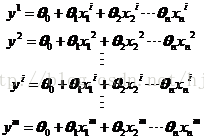


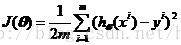
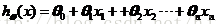
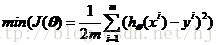
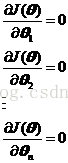

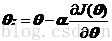
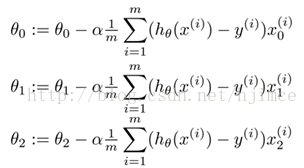
















 8691
8691

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








