1. 欧式距离Euclidean distance&&闵式距离Minkowsk distance&&绝对距离
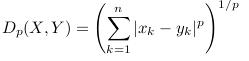
优点:平移旋转不变,
缺点:各分量之间的相关以及量纲相关
2. 马氏距离(Mahalanobis distance)
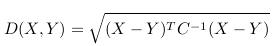
(1)优点:排除变量相关性干扰:在特征提取方面若不同特征之间相关性较大的话,用欧式距离会使得相关部分的特征值被放大。若在特征描述上需要保持每个独立特征的权重相同,则可用马氏距离。举例:现有特征组合(n1,n2,n3)可以通过主成分分析得到(m1,m2)两个相互独立的特征组合,欧式距离是n1,n2,n3权重值相同,而马氏距离是保持对于m1,m2权重值相同。
(2)优点:量纲无关,平移旋转无关,例如:Y(1)求的是X(1,:)与X(2,:)的马氏距离,Y(2)求的是X(1,:)与X(3,:)的马氏距离,依次类推
X =
1 2
1 3
2 2
3 1
Y = pdist(X,'mahal')
2.3452 2.0000 2.3452 1.2247 2.4495 1.2247
Y = pdist(X,'euclidean')
1.0000 1.0000 2.2361 1.4142 2.8284 1.4142
X =
0.1000 0.2000
0.1000 0.3000
0.2000 0.2000
0.3000 0.1000
Y = pdist(X,'mahal')
2.3452 2.0000 2.3452 1.2247 2.4495 1.2247
Y = pdist(X,'euclidean')
0.1000 0.1000 0.2236 0.1414 0.2828 0.1414
(3)协方差逆矩阵的作用:类似于加权。相关程度大的特征权重小。协方差矩阵通过总体样本计算,是不同计算特征之间的协方差。
(4)相同的两个样本放在不同的总体样本中马氏距离不同。
(5)若总体样本数小于特征数则协方差矩阵不可逆,不能用马氏距离。
3. 皮尔逊相关系数(Pearson correlation coefficient)
在马氏距离中用到协方差求不同特征之间的相关度
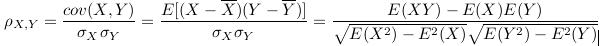
(1)p描述的是两个变量间线性相关强弱的程度。p的取值在-1与+1之间,若p>0,表明两个变量是正相关,即一个变量的值越大,另一个变量的值也会越大;若p<0,表明两个变量是负相关,即一个变量的值越大另一个变量的值反而会越小。p的绝对值越大表明相关性越强,要注意的是这里并不存在因果关系。若p=0,表明两个变量间不是线性相关,但有可能是其他方式的相关(比如曲线方式)
(2)相对于欧式距离,皮尔逊相关系数pcc能修正过大数据,pcc是判断两组数据与最佳拟合线拟合程度的一种度量。若两组数据之差始终保持一致,则相关性较大。
如在《集体智慧编程》中下图,Gene与Mick为用户,分别对图上几个电影进行评分,并得到两组评分数据,再拟合出最佳拟合线为图中虚线。
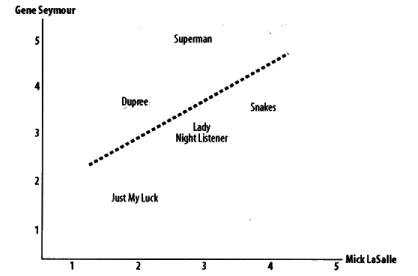
两组数据[1 2 3 4][2 3 4 5]
x =
1 2 3 4
2 3 4 5
pdist(x,'correlation')=0
pdist(x,'euclidean')=2
4. 汉明距离Hamming distance
两组数据[1 2 3 4][12 13 14 15]
x =
1 2 3 4
12 13 14 15
pdist(x,'correlation')=0
pdist(x,'euclidean')=22
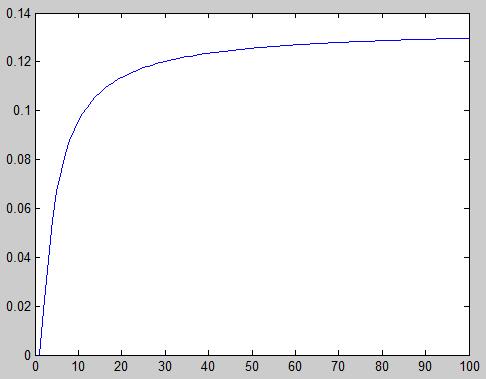
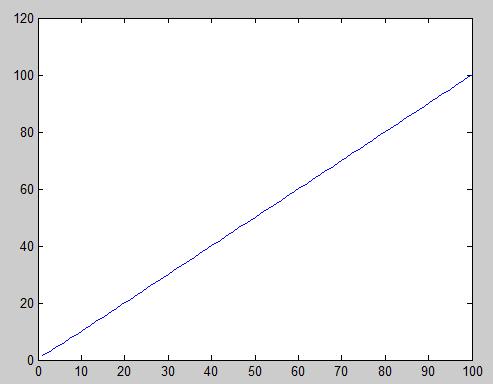
两组数据[1 2 3][2 3 m] m=4:103;证明修正夸大数据功能
皮尔逊系数在增大到夸大部分会有收敛过程,而欧氏距离没有
两个等长字符串之间的汉明距离是两个字符串对应位置的不同字符的个数
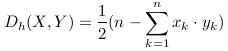
汉明距离就是表示X,Y取值不同的分量数目,上公式只适用分量只取-1或1的情况
5.Tanimoto系数(又称广义Jaccard系数)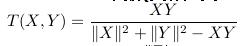
通常应用于X为布尔向量,即各分量只取0或1的时候。此时,表示的是X,Y的公共特征的占X,Y所占有的特征的比例。
A=[1,2,3,4]
B=[1,2,5]
C = A & B = [1,2]
T = Nc / ( Na + Nb -Nc) = len(c) / ( len(a) + len(b) - len(c)) = 2 / (4+3-2) = 0.4
实际上就是集合交集与并集的比。
7.余弦相似度(cosine similarity)
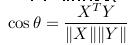
就是两个向量之间的夹角的余弦值。
应用场合:通常应用于X为布尔向量,即各分量只取0或1的时候。此时,和Tanimoto类似,是X,Y公共特征数目的测量。
优点:不受坐标轴旋转,放大缩小的影响。
还有一个调整余弦相似度(Adjusted Cosine Similarity),和余弦相似度的计算不同的是,X,Y在减去用户平均评分向量后再代入余弦相似度公式中计算。
调整余弦相似度和余弦相似度,皮尔逊相关系数在推荐系统中应用较多。在基于项目的推荐中,GroupLens有篇论文结果表明调整余弦相似度性能要优于后两者。??
8.巴氏距离
在统计学中,巴氏距离(巴塔恰里雅距离 / Bhattacharyya distance)用于测量两离散概率分布。它常在分类中测量类之间的可分离性。
在同一定义域X中,概率分布p和q的巴氏距离定义如下:其中(2)离散概率分布和(3)连续概率分布

BC是巴氏系数(Bhattacharyya coefficient)。
9. hausdroff距离
Hausdorff距离是描述两组点集之间相似程度的一种量度,它是两个点集之间距离的一种定义形式:假设有两组集合A={a1,…,ap},B={b1,…,bq},则这两个点集合之间的Hausdorff距离定义为H(A,B)=max(h(A,B),h(B,A)) (1)
其中,
h(A,B)=max(a∈A)min(b∈B)‖a-b‖ (2)
h(B,A)=max(b∈B)min(a∈A)‖b-a‖ (3)
‖·‖是点集A和B点集间的距离范式(如:L2或Euclidean距离).






















 1806
1806

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








