By: 潘云登
Date: 2009-7-21
Email: intrepyd@gmail.com
Homepage: http://blog.csdn.net/intrepyd
Copyright: 该文章版权由潘云登所有。可在非商业目的下任意传播和复制。
对于商业目的下对本文的任何行为需经作者同意。
1. 本文内容对应《算法导论》(第2版)》第13章。
2. 主要介绍了使二叉查找树保持平衡的红黑树,以及保持红黑树性质的旋转、插入和删除操作。其中,插入和删除操作较为复杂,画图分析每一种情况将有助于理解。
3. 希望本文对您有所帮助,也欢迎您给我提意见和建议。
4. 本文包含以下内容:
² 红黑树的性质
² 旋转操作
² 插入操作
² 删除操作
当二叉查找树出现不平衡,树的高度较高时,二叉查找树所支持的动态集合操作的性能可能不比用链表好。红黑树(red-black tree)是许多平衡的查找树中的一种。它保持二叉查找树性质,同时在每个结点上增加一个存储位表示结点的颜色。通过对任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有一条路径会比其它路径长出两倍,因而是接近平衡的。可以证明,一棵有n个结点的红黑树的高度至多为2 lg(n+1)。
一棵二叉查找树如果满足下面的红黑性质,则为一棵红黑树:1)每个结点或是红的,或是黑的;2)根结点是黑的;3)每个叶结点(NULL)是黑的;4)如果一个结点是红的,则它的两个儿子都是黑的;5)对每个结点,从该结点到其子孙结点的所有路径上包含相同数目的黑结点。这种黑结点的个数称为该结点的黑高度bh。
这里,叶结点(NULL)实际上是之前介绍的树结构的叶结点的子结点,该子结点指针通常赋值为NULL。为了方便处理边界条件,可以采用一个哨兵nil统一表示此类NULL结点,包括树根结点的父结点。哨兵nil的颜色为黑色。
| typedef struct node { int key; int color; struct node *left; struct node *right; struct node *parent; } rbt_node; |
红黑树的查询操作与二叉查找树相同,如关键字查询、最大关键字结点、最小关键字结点、前趋结点和后继结点等。但是,二叉查找树的插入和删除操作可能破坏红黑树性质。为保持红黑树性质,就要改变树中某些结点的颜色及指针结构。指针结构的修改是通过旋转操作来完成的。旋转操作是一种能保持二叉查找树性质的查找树局部操作,分为左旋和右旋。当在某个结点x上做左旋操作时,x为子树的根,假设它的右子结点y不是nil。在左旋之后,y成为子树新的根,x成为y的左子结点,而y的左子结点成为x的右子结点。可以看到,左旋是以某个结点到其右子结点之间的链为支轴进行。
| void left_rotate(rbt_node **root, rbt_node *x_node) { rbt_node *y_node=&nil;
y_node = x_node->right; x_node->right = y_node->left; /*将y的左子树作为x的右子树*/ if(y_node->left != &nil) y_node->left->parent = x_node; y_node->parent = x_node->parent; /*链接x的父结点和y*/ if(x_node->parent == &nil) *root = y_node; else if(x_node == x_node->parent->left) x_node->parent->left = y_node; else x_node->parent->right = y_node; y_node->left = x_node; /*使x成为y的左子结点*/ x_node->parent = y_node; } |
右旋与左旋类似。它以某个结点到其左子结点之间的链为支轴进行。当在某个结点x上做右旋操作时,x为子树的根,假设它的左子结点y不是nil。在右旋之后,y成为子树新的根,x成为y的右子结点,而y的右子结点成为x的左子结点。
| void right_rotate(rbt_node **root, rbt_node *x_node) { rbt_node *y_node=&nil;
y_node = x_node->left; x_node->left = y_node->right; /*将y的右子树作为x的左子树*/ if(y_node->right != &nil) y_node->right->parent = x_node; y_node->parent = x_node->parent; /*链接x的父结点和y*/ if(x_node->parent == &nil) *root = y_node; else if(x_node == x_node->parent->left) x_node->parent->left = y_node; else x_node->parent->right = y_node; y_node->right = x_node; /*使x成为y的右子结点*/ x_node->parent = y_node; } |
红黑树的插入操作以二叉查找树的插入操作为基础,加上一个辅助过程,用以对结点进行重新着色并旋转,从而保持红黑树性质。首先,新插入的结点z总是被着上红色。插入操作只可能破坏红黑树的性质2)或性质4),并且只会有一个性质被破坏。如果违反性质2),则发生的原因是z是根而且是红的。如果违反性质4),则原因是z和z.parent都是红的。第一种情形,只要将z重新着上黑色。第二种情形,需要分六种情况讨论。前三种与后三种相互对称,区别在于z的父结点是其祖父结点的左子结点还是右子结点。情况1)与情况2)3)的区别在于z的父结点的兄弟结点(叔叔)的颜色有所不同。所有三种情况中,z的祖父结点总是黑的,这由性质4)保证,因为z的父结点是红的。
情况1)z的叔叔y为右子结点,是红的。这时,z为当前节点,z的父结点z.parent和叔叔y都是红的,z的祖父是黑的。可以将z的父亲和叔叔都着上黑色以解决z和z.parent都是红色的问题,将z的祖父着上红色以保持性质5)。然后,把z的祖父当作当前结点,再次检查z的父结点是否为红的。换句话说,上述循环的终止条件是z的父结点为黑色。这时,z为红色,如果z的父亲为nil(黑色),即z为树根,性质2)被违反,只要将z着上黑色便可加以修正。新插入结点为树根的情况与此相同。
情况2)z的叔叔y为右子结点,是黑的,而且z是右子结点。将z设为z的父结点(z上升一层),然后对z做一次左旋操作(z下降一层),将情况2)转变为情况3)。这时,仍然只有性质4)被破坏。由于z的层数不变,z的祖父的身份保持不变。
情况3)z的叔叔y为右子结点,是黑的,而且z是左子结点。这时,z的左右子树、z的父亲的右子树,以及z的祖父的右子树(以z的叔叔为子树的根),它们的黑高度相同,性质5)成立,只有性质4)在z和z的父结点之间被破坏。通过将z的父亲着成黑色,将z的祖父着成红色,并且对z的祖父执行一次右旋操作,可以修正性质4)。所有红黑树性质得以保持,循环终止条件(z的父结点为黑的)成立。由于z原先的祖父现在成为z父结点的右子结点,树的高度减小1,这正是红黑树保持平衡的关键所在。
情况4)z的叔叔y为左子结点,是红的。与情况1)相同,将z的父亲和叔叔都着上黑色以解决z和z.parent都是红色的问题,将z的祖父着上红色以保持性质5)。然后,把z的祖父当作当前结点,再次检查z的父结点是否为红的。
情况5)z的叔叔y为左子结点,是黑的,而且z是左子结点。将z设为z的父结点(z上升一层),然后对z做一次右旋操作(z下降一层),将情况2)转变为情况6)。
情况6)z的叔叔y为左子结点,是黑的,而且z是右子结点。将z的父亲着成黑色,将z的祖父着成红色,并且对z的祖父执行一次左旋操作。所有红黑树性质得以保持。
| void rb_insert(rbt_node **root, rbt_node *z_node) { rbt_node *x_node=&nil, *y_node=&nil;
x_node = *root; while(x_node != &nil) { y_node = x_node; if(z_node->key < x_node->key) x_node = x_node->left; else x_node = x_node->right; } z_node->parent = y_node; if(y_node == &nil) *root = z_node; else if(z_node->key < y_node->key) y_node->left = z_node; else y_node->right = z_node;
z_node->left = z_node->right = &nil; z_node->color = RED; rb_insert_fixup(root, z_node); }
static void rb_insert_fixup(rbt_node **root, rbt_node *z_node) { rbt_node *y_node=&nil;
while(z_node->parent->color == RED) { if(z_node->parent == z_node->parent->parent->left) { y_node = z_node->parent->parent->right; if(y_node->color == RED) { z_node->parent->color = BLACK; /*case 1*/ y_node->color = BLACK; /*case 1*/ z_node->parent->parent->color = RED; /*case 1*/ z_node = z_node->parent->parent; /*case 1*/ } else { if(z_node == z_node->parent->right) { z_node = z_node->parent; /*case 2*/ left_rotate(root, z_node); /*case 2*/ } z_node->parent->color = BLACK; /*case 3*/ z_node->parent->parent->color = RED; /*case 3*/ right_rotate(root, z_node->parent->parent); /*case 3*/ } } else { y_node = z_node->parent->parent->left; if(y_node->color == RED) { z_node->parent->color = BLACK; /*case 4*/ y_node->color = BLACK; /*case 4*/ z_node->parent->parent->color = RED; /*case 4*/ z_node = z_node->parent->parent; /*case 4*/ } else { if(z_node == z_node->parent->left) { z_node = z_node->parent; /*case 5*/ right_rotate(root, z_node); /*case 5*/ } z_node->parent->color = BLACK; /*case 6*/ z_node->parent->parent->color = RED; /*case 6*/ left_rotate(root, z_node->parent->parent); /*case 6*/ } } } (*root)->color = BLACK; } |
红黑树的删除操作同样建立在二叉查找树的删除操作基础上。如果删除结点y是红色的,则当y被删除后,红黑树性质仍然得以保持。如果y是黑色的,则调用一个辅助函数,用来改变结点的颜色并做旋转,从而保持红黑树性质。该辅助函数的一个输入参数x是y的唯一子结点(回顾二叉查找树的删除操作),或者当y没有子结点时,x为哨兵nil。
首先,来看一下,y是黑色所产生的三个问题:1)如果y原来是根结点,而y的一个红色的子结点成为新的根,这就违反了性质2);2)如果x和y.parent(现在为x的父结点)都是红的,将违反性质4);3)删除y将导致先前包含y的任何路径上黑结点个数少1,因此,性质5)被y的一个祖先破坏了。至于前两个问题,根据性质5),可以肯定x的兄弟结点一定是哨兵nil,因此,只要让x重新着上黑色,即可保持所有的红黑树性质。
辅助函数将使用整个循环结构,重点解决问题3)。补救这个问题的一个办法是把结点x视为还有额外的一重黑色。也就是说,如果将任意包含结点x的路径上黑结点个数加1,则性质5)成立。因此,如果x为红色,将其着上黑色即可;如果x为黑色,则将它的额外的黑色沿树上移,直到1)x指向一个红色结点,将其着上黑色,或2)x为根结点,简单地消除那个、额外的黑色,或3)做必要的旋转和颜色修改,原则是保证从子树的根到每棵子树之间的黑结点并不被变换所改变。可以看到,在整个循环过程中,x总是指向具有双重黑色的那个非根结点。
循环过程中,需要分别处理八种不同情况:
情况1)x为左子结点,x的兄弟w是红色的。因为w原先是x的黑色父结点的兄弟,根据性质5),w必定有两个黑色子结点且不为nil。将w着上黑色,将x和w的父结点着上红色,并且对该父结点做一次左旋操作。这时,原先的w成为子树的根,各条路径上的黑结点个数没有被改变。同时,原先x的父亲仍然是x的父亲,但是颜色变成红色。原先w的黑色左子结点,成为新的x的兄弟结点w。情况1)转换为情况2)、3)或4)。
情况2)x为左子结点,x的兄弟w是黑色的,而且w的两个孩子都是黑色的。由于w及其两个子结点都是黑色的,可以从x和w上去掉一重黑色,从而x只有一重黑色而w为红色。为了补偿去掉的这重黑色,可以在原来是红色或黑色的x.parent上新增一重额外黑色,然后以x.parent为新的x来重复循环。可以看到,如果以情况1)进入情况2),则新结点x是红黑色的,满足循环终止条件。然后,将x着上黑色,使得子树的所有路径上的黑结点个数得到补偿。
情况3)x为左子结点,x的兄弟w是黑色的,w的左孩子是红色的,右孩子是黑色的。可以交换w和其左孩子的颜色,并对w进行右旋操作,而红黑性质仍然保持。现在x的新兄弟w是一个有红色右子结点的黑结点,情况3)转换成为情况4)。
情况4)x为左子结点,x的兄弟w是黑色的,而且w的右孩子是红色的。可以将x父结点的颜色赋给w,然后将x父结点和w的右子结点着上黑色,对x的父结点进行一次左旋操作。这时,原先x的父结点着上了额外的黑色,而且它先前的颜色并没有丢失,由新的子树的根(也是原先的w)所继承,同时,原先w的黑色被转交给它的右子结点,性质5)被修复且没有其它的性质被破坏。将x置为整棵红黑树的根后,结束循环。
情况5)-8)与插入操作一样,只要将情况1)-4)中的左右概念(包括左右子结点和左旋右旋操作)相对调即可。
| /* * 返回被删除的结点 */ rbt_node * rb_delete(rbt_node **root, rbt_node *z_node) { rbt_node *x_node=&nil, *y_node=&nil;
if(z_node->left==&nil || z_node->right==&nil) y_node = z_node; else y_node = tree_successor(z_node); if(y_node->left != &nil) x_node = y_node->left; else x_node = y_node->right; x_node->parent = y_node->parent; if(y_node->parent == &nil) *root = x_node; else if(y_node == y_node->parent->left) y_node->parent->left = x_node; else y_node->parent->right = x_node; if(y_node != z_node) /*y_node is node's successor*/ z_node->key = y_node->key;
if(y_node->color == BLACK) rb_delete_fixup(root, x_node);
return y_node; }
static void rb_delete_fixup(rbt_node **root, rbt_node *x_node) { rbt_node *w_node=&nil;
while(x_node!=*root && x_node->color==BLACK) { if(x_node==x_node->parent->left) { w_node = x_node->parent->right; if(w_node->color == RED) { w_node->color = BLACK; /*case 1*/ x_node->parent->color = RED; /*case 1*/ left_rotate(root, x_node->parent); /*case 1*/ w_node = x_node->parent->right; /*case 1*/ } if(w_node->left->color==BLACK && w_node->right->color==BLACK) { w_node->color = RED; /*case 2*/ x_node = x_node->parent; /*case 2*/ } else { if(w_node->right->color == BLACK) { w_node->left->color = BLACK; /*case 3*/ w_node->color = RED; /*case 3*/ right_rotate(root, w_node); /*case 3*/ w_node = x_node->parent->right; /*case 3*/ } w_node->color = x_node->parent->color; /*case 4*/ x_node->parent->color = BLACK; /*case 4*/ w_node->right->color = BLACK; /*case 4*/ left_rotate(root, x_node->parent); /*case 4*/ x_node = *root; /*case 4*/ } } else { w_node = x_node->parent->left; if(w_node->color == RED) { w_node->color = BLACK; /*case 5*/ x_node->parent->color = RED; /*case 5*/ right_rotate(root, x_node->parent); /*case 5*/ w_node = x_node->parent->left; /*case 5*/ } if(w_node->right->color==BLACK && w_node->left->color==BLACK) { w_node->color = RED; /*case 6*/ x_node = x_node->parent; /*case 6*/ } else { if(w_node->left->color == BLACK) { w_node->right->color = BLACK; /*case 7*/ w_node->color = RED; /*case 7*/ left_rotate(root, w_node); /*case 7*/ w_node = x_node->parent->left; /*case 7*/ } w_node->color = x_node->parent->color; /*case 8*/ x_node->parent->color = BLACK; /*case 8*/ w_node->left->color = BLACK; /*case 8*/ right_rotate(root, x_node->parent); /*case 8*/ x_node = *root; /*case 8*/ } } } x_node->color = BLACK; } |
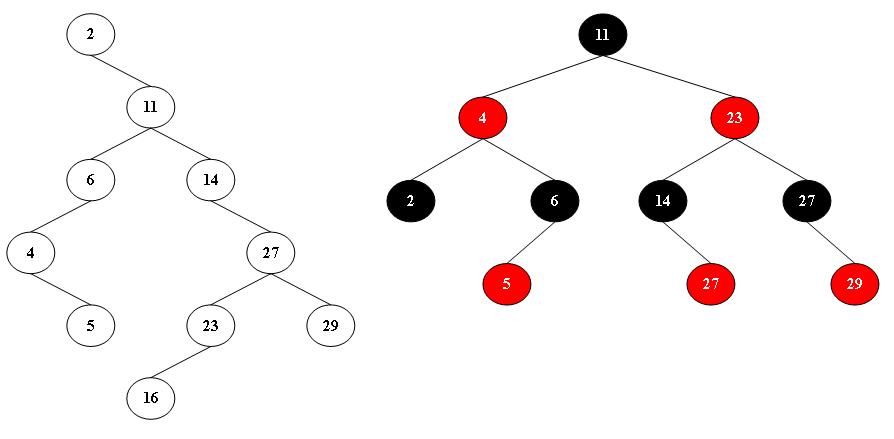
对于整数序列<2, 11, 14, 6, 4, 27, 5, 23, 29, 16>,分别用二叉查找树和红黑树的插入操作生成的树结构如下图所示。






















 3710
3710

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








