WPF中两条路径渐变的探讨

最新推荐文章于 2024-03-27 20:51:11 发布

大可山人

最新推荐文章于 2024-03-27 20:51:11 发布

阅读量7.1k

点赞数

分类专栏： C#类 WPF研究 GDI+图形类文章标签： wpf path c 算法

本文链接：https://blog.csdn.net/johnsuna/article/details/1790519

版权

C#类同时被 3 个专栏收录

186 篇文章 4 订阅

订阅专栏

GDI+图形类

123 篇文章 2 订阅

订阅专栏

WPF研究

116 篇文章 9 订阅

订阅专栏

我们在WPF中，偶尔也会涉及到两条路径作一些“路径渐变 ”。

先看看比较简单的情形：
如下图(关键点用红色圆点加以标识)：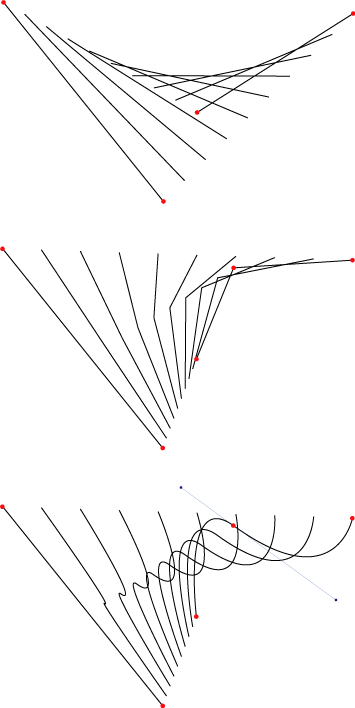
路径渐变PathBlending
（图1）

上面图1中的第1幅图可以说是最简单的路径渐变了，它由两条直线为基础，中间以插值方式作了两条直线间的渐变（插入路径数量为8，加上原始两条直线，最终共得到10条直线）。

图1中的第2幅图是将第1幅图中的右边直线从中间折起（我们称之为“拐点”），然后以此两路径（一条直线，一条折线）为基础，同样插入渐变路径条数为8,共得到10条路径，我们看到，由于拐点的作用，中间的八条路径逐渐呈现不同的拐角的折线。

图1中的第3幅图则是将第2幅的拐点变成了平滑弯曲的曲线（我们称之为“贝塞尔曲线”，关键点使用红圆点标识,贝塞尔控制点使用蓝色小圆点标识并用蓝色细线连接起来），同样插入渐变径径的条数为8，最终得到10条路径。我们发现，中间的渐变线也渐变成平滑曲线。

现在的问题是，如何实现两条给定路径的渐变呢？此问题亦可理解为：如何找到渐变线中的路径关键点及贝尔塞曲线控制点的坐标及相关点的类型（是直线拐点，中间关键点，或者是贝塞尔曲线的控制点）？

再来看看更复杂的情形：

下图2是两条曲线路径（一条红色曲线，一条是黑色曲线），我们将要说说以它们为基础的渐变。

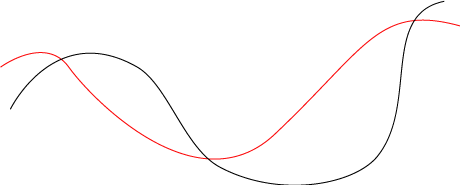
两条曲线路径
（图2）

下图3是两条路径渐变后的结果（插值路径数量为2）：

PathBlending_Blent
（图3）

为了更清晰地示意，下图4特别标示出了路径关键点（红点圆点）及贝塞尔曲线控制点（蓝色小圆点及细线）。

带关键点的路径渐变示意图
（图4）

路径渐变分析图
（图5 可以确定的是：两条路径的首/尾点渐变时得到的中间点也在两首/尾点的连接直线上并且呈均匀分布，如上图的①②、③④所示，其他的关键点/控制点则需要根据两条路径及渐变插值数量而变化）

之所以说图2至图4复杂，是因为不仅有线的形状渐变（注意两条路径的关键点的个数也是不一样的，红线为4个关键点，黑线为5个关键点），还有颜色的渐变（从红色变成为黑色）。

至此，如何找到多关键点、多控制点渐变的算法以及颜色如何进行渐变都成了新问题。

此问题解决了，下面这种更复杂的效果也就迎刃而解了：

图5 复杂曲线的渐变效果

先抛出问题，各位可以发表意见。

最后贴上图2，图3的XAML代码：

图2的XAML代码：
<Viewbox Width="459.847656" Height="184.886719"
xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation"
xmlns:x="http://schemas.microsoft.com/winfx/2006/xaml">
<Canvas Width="459.847656" Height="184.886719">

<Path StrokeThickness="1.000000" Stroke="#fffa0e0b" StrokeMiterLimit="1.000000" Data="F1 M 0.295898,66.248535 C 0.295898,66.248535 44.894531,33.529785 68.517578,66.316895 C 92.140137,99.104004 197.243164,206.331055 274.625000,133.188477 C 366.679688,46.227051 378.309570,2.718750 459.714844,25.067383"/>

<Path StrokeThickness="1.000000" Stroke="#ff000000" StrokeMiterLimit="1.000000" Data="F1 M 10.119141,108.246094 C 10.119141,108.246094 53.936523,18.998535 136.617188,66.040527 C 167.621582,83.681641 183.833008,147.156250 219.471191,166.218750 C 278.868164,197.991211 354.396484,184.117188 377.431641,155.072266 C 417.988281,103.937500 380.077148,13.126953 443.849609,0.490234"/>
</Canvas>
</Viewbox>

图3的XAML代码：
<Viewbox Width="459.847656" Height="184.885742"
xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation"
xmlns:x="http://schemas.microsoft.com/winfx/2006/xaml">
<Canvas Width="459.847656" Height="184.885742">

<Path StrokeThickness="1.000000" Stroke="#fffa0e0b" StrokeMiterLimit="1.000000" Data="F1 M 0.295898,66.248535 C 0.295898,66.248535 44.894531,33.529785 68.517578,66.316895 C 92.140137,99.104004 197.243164,206.331055 274.625000,133.188477 C 366.679688,46.227051 378.309570,2.718750 459.714844,25.067383"/>


<Path StrokeThickness="1.000000" Stroke="#ffa53d2c" StrokeMiterLimit="1.000000" Data="F1 M 3.570313,80.247559 C 3.570313,80.247559 37.239258,49.992188 64.153320,64.566406 C 77.456543,71.770020 104.818848,89.162598 138.143066,109.947266 C 176.041016,133.784180 213.795410,160.521484 256.240234,144.198242 C 298.073242,128.110352 340.344727,110.023438 361.418945,87.477051 C 396.536133,49.690430 399.673828,11.891602 454.426758,16.875000"/>
<Path StrokeThickness="1.000000" Stroke="#ff523930" StrokeMiterLimit="1.000000" Data="F1 M 6.844727,94.247070 C 6.844727,94.247070 32.607910,68.570313 59.788574,62.816406 C 76.693848,59.237793 103.965820,67.975586 137.380371,87.994141 C 171.875000,108.659180 201.500000,143.897461 237.855469,155.208984 C 287.819336,170.753906 347.370117,147.070313 369.425781,121.274414 C 407.261719,76.813965 389.875977,12.509277 449.137695,8.682617"/>


<Path StrokeThickness="1.000000" Stroke="#ff000000" StrokeMiterLimit="1.000000" Data="F1 M 10.119141,108.246094 C 10.119141,108.246094 53.936523,18.998535 136.617188,66.040527 C 167.621582,83.681641 183.833008,147.156250 219.471191,166.218750 C 278.868164,197.991211 354.396484,184.117188 377.431641,155.072266 C 417.988281,103.937500 380.077148,13.126953 443.849609,0.490234"/>
</Canvas>
</Viewbox>