KMP算法,是由Knuth,Morris,Pratt共同提出的模式匹配算法,其对于任何模式和目标序列,都可以在线性时间内完成匹配查找,而不会发生退化,是一个非常优秀的模式匹配算法。但是相较于其他模式匹配算法,该算法晦涩难懂,第一次接触该算法的读者往往会看得一头雾水,主要原因是KMP算法在构造跳转表next过程中进行了多个层面的优化和抽象,使得KMP算法进行模式匹配的原理显得不那么直白。本文希望能够深入KMP算法,将该算法的各个细节彻底讲透,扫除读者对该算法的困扰。
KMP算法对于朴素匹配算法的改进是引入了一个跳转表next[]。以模式字符串abcabcacab为例,其跳转表为:
| j | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| pattern[j] | a | b | c | a | b | c | a | c | a | b |
| next[j] | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 5 | 0 | 1 |
举例说明,如下是使用上例的模式串对目标串执行匹配的步骤
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| b | a | b | c | b | a | b | c | a | b | c | a | a | b | c | a | b | c | a | b | c | a | c | a | b | c |
| a | b | c | a | b | c | a | c | a | b | ||||||||||||||||
| a | b | c | a | b | c | a | c | a | b | ||||||||||||||||
| a | b | c | a | b | c | a | c | a | b | ||||||||||||||||
| a | b | c | a | b | c | a | c | a | b | ||||||||||||||||
| a | b | c | a | b | c | a | c | a | b | ||||||||||||||||
| a | b | c | a | b | c | a | c | a | b |
next跳转表,在进行模式匹配,实现模式串向后移动的过程中,发挥了重要作用。这个表看似神奇,实际从原理上讲并不复杂,对于模式串而言,其前缀字符串,有可能也是模式串中的非前缀子串,这个问题我称之为前缀包含问题。以模式串abcabcacab为例,其前缀4 abca,正好也是模式串的一个子串abc(abca)cab,所以当目标串与模式串执行匹配的过程中,如果直到第8个字符才匹配失败,同时也意味着目标串当前字符之前的4个字符,与模式串的前4个字符是相同的,所以当模式串向后移动的时候,可以直接将模式串的第5个字符与当前字符对齐,执行比较,这样就实现了模式串一次性向前跳跃多个字符。所以next表的关键就是解决模式串的前缀包含。当然为了保证程序的正确性,对于next表的值,还有一些限制条件,后面会逐一说明。
如何以较小的代价计算KMP算法中所用到的跳转表next,是算法的核心问题。这里我们引入一个概念f(j),其含义是,对于模式串的第j个字符pattern[j],f(j)是所有满足使pattern[1...k-1] = pattern[j-(k-1)...j - 1](k < j)成立的k的最大值。还是以模式串abcabcacab为例,当处理到pattern[8] = 'c'时,我们想找到'c'前面的k-1个字符,使得pattern[1...k-1] = pattern[8-(k-1)...7],这里我们可以使用一个笨法,让k-1从1到6递增,然后依次比较,直到找到最大值的k为止,比较过程如下
| k-1 | 前缀 | 关系 | 子串 |
| 1 | a | == | a |
| 2 | ab | != | ca |
| 3 | abc | != | bca |
| 4 | abca | == | abca |
| 5 | abcab | != | cabca |
| 6 | abcabc | != | bcabca |
| j | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| pattern[j] | a | b | c | a | b | c | a | c | a | b |
| next[j] | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 5 | 0 | 1 |
| f(j) | 0 | 1 | 1 | 1 | 2 | 3 | 4 | 5 | 1 | 2 |
如果 pattern[j] != pattern[f(j)],next[j] = f(j);
如果 pattern[j] = pattern[f(j)],next[j] = next[f(j)];
当要求f(9)时,f(8)和next[8]已经可以得到,此时我们可以考察pattern[next[8]],根据前面对于next值的计算方式,我们知道pattern[8] != pattern[next[8]]。我们的目的是要找到pattern[9]的包含前缀,而pattern[8] != pattern[5],pattern[1...5]!=pattern[4...8]。我们继续考察pattern[next[5]]。如果pattern[8]
= pattern[next[5]],假设next[5] = 3,说明pattern[1...2] = pattern[6...7],且pattern[3] = pattern[8],此时对于pattern[9]而言,就有pattern[1...3]=pattern[6...8],我们就找到了f(9) = 4。这里我们考察的是pattern[next[j]],而不是pattern[f(j)],这是因为对于next[]而言,pattern[j] != pattern[next[j]],而对于f()而言,pattern[j]与pattern[f(j)]不一定不相等,而我们的目的就是要在pattern[j]
!= pattern[f(j)]的情况下,解决f(j+1)的问题,所以使用next[j]向前回溯,是正确的。
现在,我们来总结一下next[j]和f(j)的关系,next[j]是所有满足pattern[1...k - 1] = pattern[(j - (k - 1))...j -1](k < j),且pattern[k] != pattern[j]的k中,k的最大值。而f(j)是满足pattern[1...k - 1] = pattern[(j - (k - 1))...j -1](k < j)的k中,k的最大值。还是以上例的模式来说,对于第7个元素,其f(j) = 4, 说明pattern[7]的前3个字符与模式的前缀3相同,但是由于pattern[7] = pattern[4], 所以next[7] != 4。
通过以上这些,读者可能会有疑问,为什么不用f(j)直接作为KMP算法的跳转表呢?实际从程序正确性的角度讲是可以的,但是使用next[j]作为跳转表更加高效。还是以上面的模式为例,当target[n]与pattern[7]发生匹配失败时,根据f(j),target[n]要继续与pattern[4]进行比较。但是在计算f(8)的时候,我们会得出pattern[7]
= pattern[4],所以target[n]与pattern[4]的比较也必然失败,所以target[n]与pattern[4]的比较是多余的,我们需要target[n]与更小的pattern进行比较。当然使用f(j)作为跳转表也能获得不错的性能,但是KMP三人将问题做到了极致。
我们可以利用f(j)作为媒介,来递推模式的跳转表next。算法如下:
inline void BuildNext(const char* pattern, size_t length, unsigned int* next)
{
unsigned int i, t;
i = 1;
t = 0;
next[1] = 0;
while(i < length + 1)
{
while(t > 0 && pattern[i - 1] != pattern[t - 1])
{
t = next[t];
}
++t;
++i;
if(pattern[i - 1] == pattern[t - 1])
{
next[i] = next[t];
}
else
{
next[i] = t;
}
}
//pattern末尾的结束符控制,用于寻找目标字符串中的所有匹配结果用
while(t > 0 && pattern[i - 1] != pattern[t - 1])
{
t = next[t];
}
++t;
++i;
next[i] = t;
}
程序中,9到27行的循环需要特别说明一下,我们发现在循环开始之后,就没有再为t赋新值,也就是说,对于计算next[j]时的t值,在计算next[j+1]时,还会用得着。实际这时的t的就等于f(j)。还是以上例的目标串为例,当j等于1,我们可以得出t = f(2) = 1。使用归纳法,当计算完next[j]后,我们假设此时t=f(j),此时第11~14行的循环就是要找到满足pattern[k] = pattern[j]的最大k值。如果这样的k存在,对于pattern[j+1]而言,其前k个元素,与模式的前缀k相同。此时的t+1就是f(j+1)。这时我们就要判断pattern[j+1]和pattern[t](t = t+1)的关系,然后求出next[j+1]。这里需要初始条件next[1] = 0。
利用跳转表实现字符串匹配的算法如下:
unsigned int KMP(const char* text, size_t text_length, const char* pattern, size_t pattern_length, unsigned int* matches)
{
unsigned int i, j, n;
unsigned int next[pattern_length + 2];
BuildNext(pattern, pattern_length, next);
i = 0;
j = 1;
n = 0;
while(pattern_length + 1 - j <= text_length - i)
{
if(text[i] == pattern[j - 1])
{
++i;
++j;
//发现匹配结果,将匹配子串的位置,加入结果
if(j == pattern_length + 1)
{
matches[n++] = i - pattern_length;
j = next[j];
}
}
else
{
j = next[j];
if(j == 0)
{
++i;
++j;
}
}
}
//返回发现的匹配数
return n;
}
该算法在原有基础上进行了扩展,在原模式串末尾加入了一个“空字符”,“空字符”不等于任何的可输入字符,当目标串匹配至“空字符”时,说明已经在目标字符串中发现了模式,将模式串在目标串中的位置,加入matchs[]数组中,同时判定为匹配失败,并根据“空字符”的next值,跳转到适当位置,这样算法就可以识别出字符串中所有的匹配子串。
最后,对KMP算法的正确性做一简要说明,还是以上文的模式串pattern和目标串target为例,假设已经匹配到第3部的位置,且在target[13]处发现匹配失败,我们如何决定模式串的滑动步数,来保证既要忽略不必要的多余比较,又不漏过可能的匹配呢?
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | |
| target | b | a | b | c | b | a | b | c | a | b | c | a | a | b | c | a | b | c | a | b | c | a | c | a | b | c |
| pattern | a | b | c | a | b | c | a | c | a | b |
对于例子中的情况,显然向后移动多于3个字符有可能会漏过target[9...18]这样的的可能匹配。但是为什么向后移动1个或者2个字符是不必要的多余比较呢?当target[13]与pattern[8]匹配失败时,同时也意味着,target[6...12]
= pattern[1...7],而next[8]=5,意味着,pattern[1...4] = pattern[4...7],pattern[1...5]
!= pattern[3...7],pattern[1...6]
!= pattern[2...7]。如果我们将模式串后移1个字符,使pattern[7]与target[13]对齐,此时target[7...12]相当于pattern[2...7],且target[7...12]与pattern[1..6]逐个对应,而我们已经知道pattern[1...6]
!= pattern[2...7]。所以不管target[13]是否等于pattern[7],此次比较都必然失败。同理向前移动2个字符也是多余的比较。由此我们知道当在pattern[j]处发生匹配失败时,将当前输入字符与pattern[j]和pattern[next[j]]之间的任何一个字符对齐执行的匹配尝试都是必然失败的。这就说明,在模式串从目标串头移动到目标串末尾的过程中,除了跳过了必然失败的情况之外,没有漏掉任何一个可能匹配,所以KMP算法的正确性是有保证的。
后记:
- 首先要感谢Knuth-Morris-Pratt那篇光辉的论文《Fast Pattern Matching In Strings》,让我们在字符串处理的道路上看得更远。本文的例子和思路,均完全来自这篇论文,论文后面还对KMP算法的时间复杂度进行了彻底的分析。
- KMP算法是一个高度优化的精妙算法,所以初涉该算法的时候,不要指望一蹴而就,一下子就将KMP算法理解透,而是应该循序渐进,逐步加深理解。据说该算法是Knuth,Morris,Pratt三人分别独立发现的,我斗胆揣测一下该算法的演进历程。首先应该是发现了模式串前缀的自包含问题,然后是提出了f(j)的概念,然后是搞定了如何计算f(j),然后提出了next[j]的概念,然后搞定了如何用f(j)计算next[j+1],然后是只用f(j)做中间结果直接算出next[j+1]。之所以我会这么猜测,主要是因为next跳转表的概念和生成算法太高端,中间经历了多个转换,极难一步到位想出来这么搞。所以我们也应该按照这个流程来学习KMP算法,而如何计算f(j)则是整个算法的精髓所在。
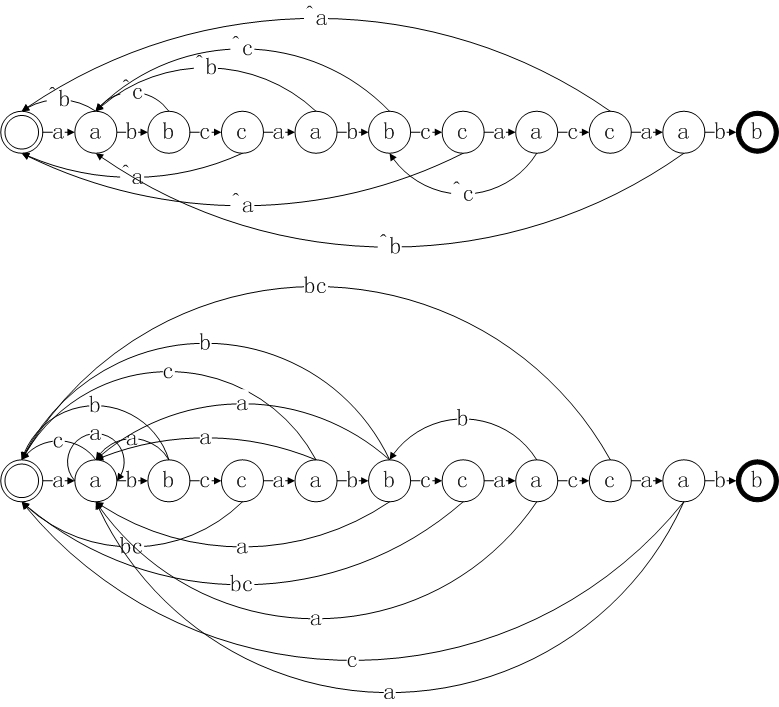
- 实际上,KMP算法中所用到的跳转表next是一个简化了的DFA,对于DFA而言,其跳转和输入的字符集有关,而KMP算法中的跳转表,对于模式串中的当前位置j-1,只有两种跳转方式pattern[j],和^pattern[j],所以KMP算法的跳转功能要弱于DFA,但是其构建速度,又大大快于DFA,在花费较小代价的同时,取得了逼近DFA的效果。下面是对于文中使用的模式串生成跳转表(上)和DFA的比较,显然DFA要复杂的多(这个是我手画的如果有画错的地方,请读者不吝赐教)。
 深入理解KMP算法:模式匹配的高效之道
深入理解KMP算法:模式匹配的高效之道





















 1万+
1万+










