对于给定的集合A{a1,a2,...,an},其中的n个元素互不相同,如何输出这n个元素的所有排列(全排列)。
递归算法
这里以A{a,b,c}为例,来说明全排列的生成方法,对于这个集合,其包含3个元素,所有的排列情况有3!=6种,对于每一种排列,其第一个元素有3种选择a,b,c,对于第一个元素为a的排列,其第二个元素有2种选择b,c;第一个元素为b的排列,第二个元素也有2种选择a,c,……,依次类推,我们可以将集合的全排列与一棵多叉树对应。如下图所示
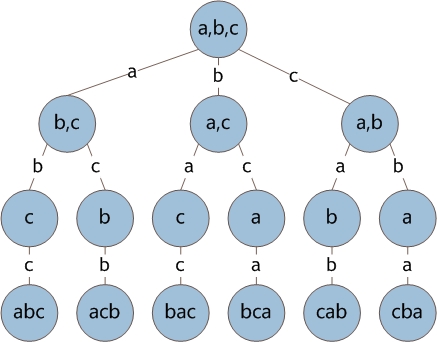
在此树中,每一个从树根到叶子节点的路径,就对应了集合A的一个排列。通过递归算法,可以避免多叉树的构建过程,直接生成集合A的全排列,代码如下。
template <typename T>
inline void swap(T* array, unsigned int i, unsigned int j)
{
T t = array[i];
array[i] = array[j];
array[j] = t;
}
/*
* 递归输出序列的全排列
*/
void FullArray(char* array, size_t array_size, unsigned int index)
{
if(index >= array_size)
{
for(unsigned int i = 0; i < array_size; ++i)
{
cout << array[i] << ' ';
}
cout << '\n';
return;
}
for(unsigned int i = index; i < array_size; ++i)
{
swap(array, i, index);
FullArray1(array, array_size, index + 1);
swap(array, i, index);
}
}
字典序
全排列生成算法的一个重要思路,就是将集合A中的元素的排列,与某种顺序建立一一映射的关系,按照这种顺序,将集合的所有排列全部输出。这种顺序需要保证,既可以输出全部的排列,又不能重复输出某种排列,或者循环输出一部分排列。字典序就是用此种思想输出全排列的一种方式。这里以A{1,2,3,4}来说明用字典序输出全排列的方法。
首先,对于集合A的某种排列所形成的序列,字典序是比较序列大小的一种方式。以A{1,2,3,4}为例,其所形成的排列1234<1243,比较的方法是从前到后依次比较两个序列的对应元素,如果当前位置对应元素相同,则继续比较下一个位置,直到第一个元素不同的位置为止,元素值大的元素在字典序中就大于元素值小的元素。上面的a1[1...4]=1234和a2[1...4]=1243,对于i=1,i=2,两序列的对应元素相等,但是当i=2时,有a1[2]=3<a2[2]=4,所以1234<1243。
使用字典序输出全排列的思路是,首先输出字典序最小的排列,然后输出字典序次小的排列,……,最后输出字典序最大的排列。这里就涉及到一个问题,对于一个已知排列,如何求出其字典序中的下一个排列。这里给出算法。
- 对于排列a[1...n],找到所有满足a[k]<a[k+1](0<k<n-1)的k的最大值,如果这样的k不存在,则说明当前排列已经是a的所有排列中字典序最大者,所有排列输出完毕。
- 在a[k+1...n]中,寻找满足这样条件的元素l,使得在所有a[l]>a[k]的元素中,a[l]取得最小值。也就是说a[l]>a[k],但是小于所有其他大于a[k]的元素。
- 交换a[l]与a[k].
- 对于a[k+1...n],反转该区间内元素的顺序。也就是说a[k+1]与a[n]交换,a[k+2]与a[n-1]交换,……,这样就得到了a[1...n]在字典序中的下一个排列。
这里我们以排列a[1...8]=13876542为例,来解释一下上述算法。首先我们发现,1(38)76542,括号位置是第一处满足a[k]<a[k+1]的位置,此时k=2。所以我们在a[3...8]的区间内寻找比a[2]=3大的最小元素,找到a[7]=4满足条件,交换a[2]和a[7]得到新排列14876532,对于此排列的3~8区间,反转该区间的元素,将a[3]-a[8],a[4]-a[7],a[5]-a[6]分别交换,就得到了13876542字典序的下一个元素14235678。下面是该算法的实现代码
/*
* 将数组中的元素翻转
*/
inline void Reverse(unsigned int* array, size_t array_size)
{
for(unsigned i = 0; 2 * i < array_size - 1; ++i)
{
unsigned int t = array[i];
array[i] = array[array_size - 1 - i];
array[array_size - 1 - i] = t;
}
}
inline int LexiNext(unsigned int* lexinum, size_t array_size)
{
unsigned int i, j, k, t;
i = array_size - 2;
while(i != UINT_MAX && lexinum[i] > lexinum[i + 1])
{
--i;
}
//达到字典序最大值
if(i == UINT_MAX)
{
return 1;
}
for(j = array_size - 1, k = UINT_MAX; j > i; --j)
{
if(lexinum[j] > lexinum[i])
{
if(k == UINT_MAX)
{
k = j;
}
else
{
if(lexinum[j] < lexinum[k])
{
k = j;
}
}
}
}
t = lexinum[i];
lexinum[i] = lexinum[k];
lexinum[k] = t;
Reverse(lexinum + i + 1, array_size - i - 1);
return 0;
}
/*
* 根据字典序输出排列
*/
inline void ArrayPrint(const char* array, size_t array_size, const unsigned int* lexinum)
{
for(unsigned int i = 0; i < array_size; ++i)
{
cout << array[lexinum[i]] << ' ';
}
cout << '\n';
}
/*
* 基于逆序数的全排列输出
*/
void FullArray(char* array, size_t array_size)
{
unsigned int lexinumber[array_size];
for(unsigned int i = 0; i < array_size; ++i)
{
lexinumber[i] = i;
}
ArrayPrint(array, array_size, lexinumber);
while(!LexiNext(lexinumber, array_size))
{
ArrayPrint(array, array_size, lexinumber);
}
}字典序算法还有一个优点,就是不受重复元素的影响。例如1224,交换中间的两个2,实际上得到的还是同一个排列,而字典序则是严格按照排列元素的大小关系来生成的。对于包含重复元素的输入集合,需要先将相同的元素放在一起,以集合A{a,d,b,c,d,b}为例,如果直接对其索引123456进行全排列,将不会得到想要的结果,这里将重复的元素放到相邻的位置,不同元素之间不一定有序,得到排列A'{a,d,d,b,b,c},然后将不同的元素,对应不同的索引值,生成索引排列122334,再执行全排列算法,即可得到最终结果。





















 7345
7345

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








