网上关于FFT在信号处理中应用的文章并不少,这里尽量少说废话,直接说如何用FFT实现多项式乘法。
多项式乘法,通常是用系数乘积的方式完成,这样的时间复杂度是O(n^2) n为多项式项数。系数乘法可以满足大多数的乘法需求,然而当位数大于1000时,此法用起来就显得捉襟见肘
通过引入FFT,我们可以将这个复杂度降到O(nlogn)
基本概念
1.多项式的两种表示法
系数表示法:即平时看到的多项式:Σi=0~n-1 a[i]*(x^i)
点值表示法:一个最高次为n-1次的多项式f(x),可以表示为n个其图像上点(x,y),例如2x^2+3x+1可以表示为(0,1) (1,6) (2,15)
两种方法可以互相转换,而点值表示法下两多项式相乘是非常方便的,只要将同一个x对应的两式y值相乘,就是新多项式对应的点值,当然,所取点值数量需要与结果多项式相符,例如:
(x+1)*(2x+1) = 2x^2+3x+1
x+1 -> (0,1) (1,2) (2,3)
2x+1 -> (0,1) (1,3) (2,5)
{(0,1) (1,2) (2,3)}*{(0,1) (1,3) (2,5)} -> (0,1) (1,6) (2,15) -> 2x^2+3x+1
而两种表示法的转换就是DFT(离散傅里叶变换,Discrete Fourier Transform)和IDFT(逆离散傅里叶变换,Inversed Discrete Fourier Transform),但是基于实数的DFT和IDFT效率仍为n^2,在此不做累述
2.复根
既然实数不行,那么我们就用性质特殊的虚数。如果读者不知道虚数,也许问题也不大,把i当成一个具有特别性质的数学符号来理解吧
在本文中,我们定义n次复根为满足x^n=1的复数x,其中n为正整数。如4次复根有4个,分别是 1,i,-1,-i。
由欧拉公式e^(ix)=(cos x+isin x),我们可以得到e^(2πi)=1。那么若k为整数,e^(2kπi/n)就是一个n次复根。为方便表述,我们定义w(n,k)=e^(2kπi/n)。通过欧拉公式,我们也可以将e的指数幂形式转化为我们熟知的a+bi形式(后文并不需要这个转化,这里提到是为了提醒读者:我们所说的复根仍然是普通的复数)。
复根有一些特殊性质,所以可以加速DFT和IDFT
1、w(n,2*k)=w(n/2,k) //n为偶数
2、w(n,k)=-w(n,k+n/2) //n为偶数
理解了如上性质以后,就可以开始学习FFT了
快速傅里叶变换
原理
快速傅里叶之所以快,就是因为它使用分治策略,将多项式分为奇次项和偶次项处理。
对于A(x)=a[0]+a[1]*x+a[2]*x^2+...+a[n-1]x^(n-1) //n为偶数
设O(x)=a[1]+a[3]*x+a[5]*x^2+...+a[n-1]x^(n/2-1)
E(x)=a[0]+a[2]*x+a[4]*x^2+...+a[n-2]x^(n/2-1)
则有A(x)=x*O(x^2)+E(x^2)
FFT将n次复根{w(n,0),w(n,1)...w(n,n-1)}作为点值的x,根据复根性质1,x^2=(w(n,k))^2=w(n/2,k) 于是,结合上面的式子,我们成功地将n项问题转化为了n/2项问题
那么k大于n/2时怎么办呢?由复根性质2,w(n,k-n/2)=-w(n,k) 所以w(n,k)^2=w(n,k-n/2)^2,只要计算出w(n,k-n/2)对应的O和E函数值,w(n,k)也就自然求出了,这就是所谓的蝴蝶操作
分治的终点是当n=1,y[i]=a[i]*w(1,0)=a[i],时间效率O(nlogn)
因为每次分治都需要n为偶数,n必须为2的幂,如果不足就补上系数为0的项
根据如上叙述,可以写出fft的递归实现方法,虽然后面的迭代实现更为优秀,但是强烈建议先理解递归算法,因为这是理解FFT的基础
递归快速傅里叶变换的伪代码
RECURSIVE-FFT(a)
n=a.length
if n==1
return a
E={a[0],a[2],...,a[n-2]}
O=(a[1],a[3],...,a[n-1]}
y_E=RECURSIVE-FFT(E);
y_O=RECURSIVE-FFT(O);
for k=0 to n/2-1
w=e^(2πki/n)
y[k]=y_E[k]+w*y_O[k]
y[k+n/2]=y_E[k]-w*y_O[k]
return y
其中a为系数向量,返回的y数组即为n次复根对应的n个值
高效FFT实现
上述代码花费了大量空间用于创建和维护数组,而我们可以使用迭代法避免这一部分的空间使用
为了迭代,首先数组被分治到的部分必须连续,观察递归调用的过程可以发现,分治是按照二进制的末位开始分类的,如n=8时,分治顺序如下
0,1,2,3,4,5,6,7
(0,2,4,6)(1,3,5,7)
(0,4)(2,6)(1,5)(3,7)
写成二进制000,100,010,110,001,101,011,111
将二进制翻转000,001,010,011,100,101,110,111这不正是0~7的单增序列吗?
原理是翻转后末位变首位,而高位恰恰决定了数的大小
于是我们递推预处理出rev数组
void get_rev(int bit)
{
for(int i=0;i<(1<<bit);i++)
rev[i]=(rev[i>>1]>>1)|((i&1)<<(bit-1));
}
然后根据rev对a重新排序,就可以进行迭代fft了,我们已知含一个元素的DFT为系数本身,那么将其按次序使用蝴蝶操作两两合并就能得到两个元素的DFT,然后再合并得到四元素DFT,以此类推,就可以得到整个式子的DFT
typedef complex<double> cd;//C++ 自带复数类,需要头文件complex
void fft(cd *a,int n)
{
for(int i=0;i<n;i++) if(i<rev[i]) swap(a[i],a[rev[i]]);
for(int step=1;step<n;step<<=1)
{
cd wn=exp(cd(0,PI/step));//exp:e的幂,此处计算单位根
for(int j=0;j<n;j+=step<<1)
{
cd wnk(1,0);//cd构造函数:cd(实数部分,虚数部分/i);
for(int k=j;k<j+step;k++)
{//蝴蝶操作
cd x=a[k];
cd y=wnk*a[k+step];
a[k]=x+y;
a[k+step]=x-y;
wnk*=wn;
}
}
}
}
至此,DFT已经实现完成了,那么IDFT呢?
DFT的过程中,我们实际上相当于给系数向量a乘上了一个矩阵,如下图
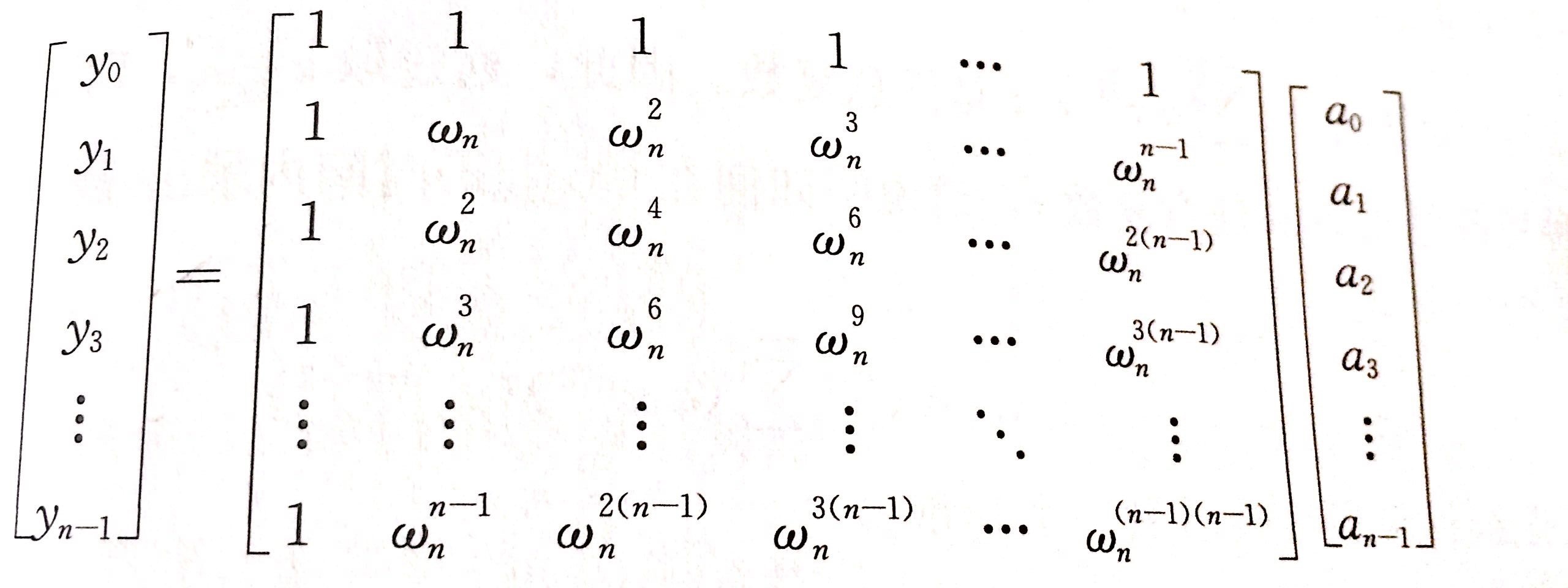
那么我们只需乘上它的逆矩阵即可
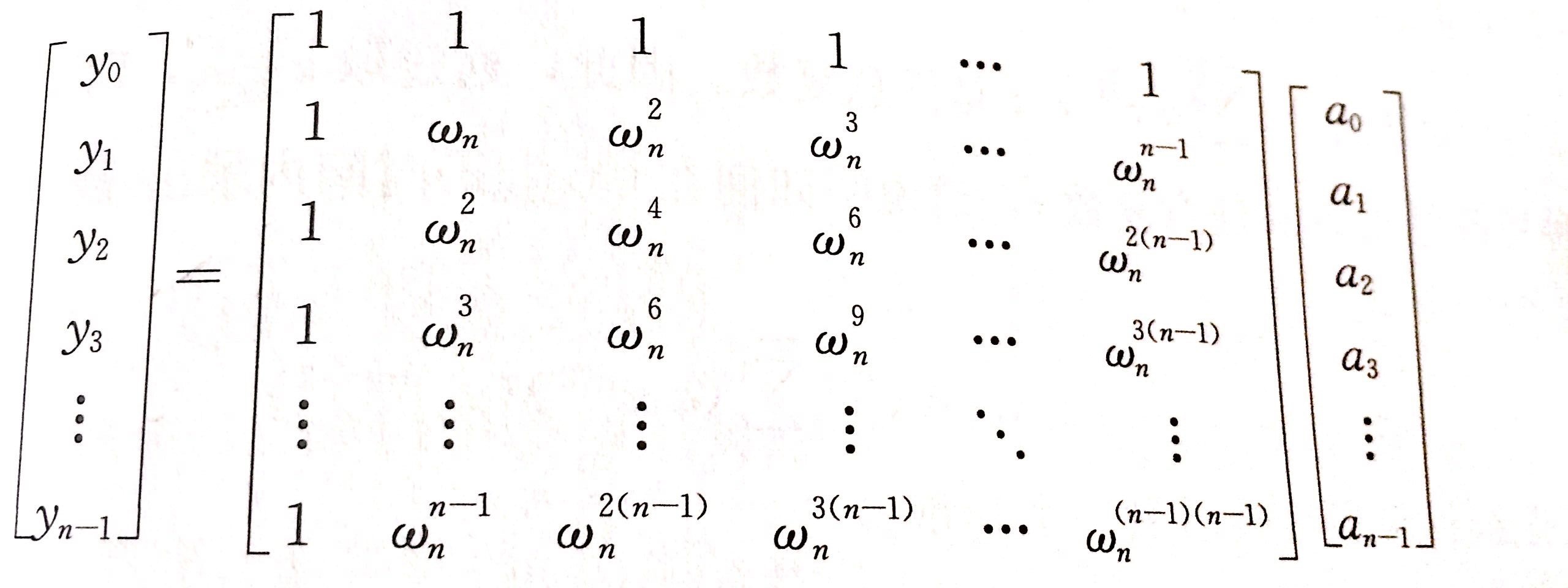
那么我们只需乘上它的逆矩阵即可
可以证明,对于矩阵每一项取倒数再除以n就是该矩阵的逆矩阵
于是含IDFT的FFT代码如下,当计算DFT时传入参数1,计算IDFT时传入-1
void fft(cd *a,int n,int dft)
{
for(int i=0;i<n;i++) if(i<rev[i]) swap(a[i],a[rev[i]]);
for(int step=1;step<n;step<<=1)
{
cd wn=exp(cd(0,dft*PI/step));
for(int j=0;j<n;j+=step<<1)
{
cd wnk(1,0);
for(int k=j;k<j+step;k++)
{
cd x=a[k];
cd y=wnk*a[k+step];
a[k]=x+y;
a[k+step]=x-y;
wnk*=wn;
}
}
}
if(dft==-1) for(int i=0;i<n;i++) a[i]/=n;
}
最后附上FFT计算高精度乘法的代码,高精度乘法的每一位都可以看做是多项式的一个系数,只不过需要注意进位操作
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<complex>
using namespace std;
int n;
typedef complex<double> cd;
#define maxl 2097153
#define PI 3.14159265358979
char s1[maxl],s2[maxl];
cd a[maxl];
cd b[maxl];
int rev[maxl];
void get_rev(int bit)
{
for(int i=0;i<(1<<bit);i++)
rev[i]=(rev[i>>1]>>1)|((i&1)<<(bit-1));
}
void fft(cd *a,int n,int dft)
{
for(int i=0;i<n;i++) if(i<rev[i]) swap(a[i],a[rev[i]]);
for(int step=1;step<n;step<<=1)
{
cd wn=exp(cd(0,dft*PI/step));
for(int j=0;j<n;j+=step<<1)
{
cd wnk(1,0);
for(int k=j;k<j+step;k++)
{
cd x=a[k];
cd y=wnk*a[k+step];
a[k]=x+y;
a[k+step]=x-y;
wnk*=wn;
}
}
}
if(dft==-1) for(int i=0;i<n;i++) a[i]/=n;
}
int output[maxl];
int main()
{
//freopen("fft.in","r",stdin);
scanf("%s%s",s1,s2);
int l1=strlen(s1);
int l2=strlen(s2);
int s=2,bit=1;
for(bit=1;(1<<bit)<l1+l2-1;bit++)s<<=1;//maybe wiping the"-1" is better
for(int i=0;i<l1;i++) a[i]=(double)(s1[l1-i-1]-'0');
for(int i=0;i<l2;i++) b[i]=(double)(s2[l2-i-1]-'0');
//for(int i=0;i<8;i++) printf("%d %d\n",i,rev[i]);
get_rev(bit);
fft(a,s,1);
fft(b,s,1);
for(int i=0;i<s;i++) a[i]*=b[i];
fft(a,s,-1);
for(int i=0;i<s;i++)
{
output[i]+=(int)(a[i].real()+0.5);//取实数四舍五入,此时虚数部分应当为0或由于浮点误差接近0
output[i+1]+=output[i]/10;
output[i]%=10;
}
int i;
for(i=l1+l2;!output[i]&&i>=0;i--);
if(i==-1) printf("0");
for(;i>=0;i--) printf("%d",output[i]);
putchar('\n');
}








 本文探讨如何利用快速傅里叶变换(FFT)将多项式乘法的时间复杂度从O(n^2)降低到O(nlogn),详细介绍了FFT的基本概念,包括多项式的表示法和复根,并讲解了FFT的原理及递归实现的伪代码。
本文探讨如何利用快速傅里叶变换(FFT)将多项式乘法的时间复杂度从O(n^2)降低到O(nlogn),详细介绍了FFT的基本概念,包括多项式的表示法和复根,并讲解了FFT的原理及递归实现的伪代码。
















 4012
4012

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








