有1亿个不重复的64位的01字符串,任意给出一个64位的01字符串f,如何快速从中找出与f汉明距离小于3的字符串?
大规模网页的近似查重
主要翻译自WWW07的Detecting Near-Duplicates for Web Crawling
WWW上存在大量内容近似相同的网页,对搜索引擎而言,去除近似相同的网页可以提高检索效率、降低存储开销。
当爬虫在抓取网页时必须很快能在海量文本集中快速找出是否有重复的网页。
论文主要2个贡献:
1. 展示了simhash可以用以海量文本查重
2. 提出了一个在实际应用中可行的算法。
两篇文本相似度普遍的定义是比较向量化之后两个词袋中词的交集程度,有cosine,jaccard等等
如果直接使用这种计算方式,时间空间复杂度都太高,因此有了simhash这种降维技术,
但是如何从传统的向量相似度能用simhash来近似,论文没提,应该是有很长一段推导要走的。
Simhash算法
一篇文本提取出内容以后,经过基本的预处理,比如去除停词,词根还原,甚至chunking,最后可以得到一个向量。
对每一个term进行hash算法转换,得到长度f位的hash码,每一位上1-0值进行正负权值转换,例如f1位是1时,权值设为 +weight, fk位为0时,权值设为-weight。
讲文本中所有的term转换出的weight向量按f对应位累加最后得到一个f位的权值数组,位为正的置1,位为负的置0,那么文本就转变成一个f位的新1-0数组,也就是一个新的hash码。

Simhash具有两个“冲突的性质”:
1. 它是一个hash方法
2. 相似的文本具有相似的hash值,如果两个文本的simhash越接近,也就是汉明距离越小,文本就越相似。
因此海量文本中查重的任务转换位如何在海量simhash中快速确定是否存在汉明距离小的指纹。
也就是:在n个f-bit的指纹中,查询汉明距离小于k的指纹。
在文章的实验中(见最后),simhash采用64位的哈希函数。在80亿网页规模下汉明距离=3刚好合适。
因此任务的f-bit=64 , k=3 , n= 8*10^11
任务清晰,首先看一下两种很直观的方法:
1. 对输入指纹,枚举出所有汉明距离小于3的simhash指纹,对每个指纹在80亿排序指纹中查询。
(这种方法需要进行C(64,3)=41664次的simhash指纹,再为每个进行一次查询)
2. 输入指纹不变,对应集合相应位置变。也就是集合上任意3位组合的位置进行变化,实际上就是提前准备41664个排序可能,需要庞大的空间。输入在这群集合并行去搜....
提出的方法介于两者之间,合理的空间和时间的折中。
• 假设我们有一个已经排序的容量为2d,f-bit指纹集。看每个指纹的高d位。该高低位具有以下性质:尽管有很多的2d位组合存在,但高d位中有只有少量重复的。
• 现在找一个接近于d的数字d’,由于整个表是排好序的,所以一趟搜索就能找出高d’位与目标指纹F相同的指纹集合f’。因为d’和d很接近,所以找出的集合f’也不会很大。
• 最后在集合f’中查找和F之间海明距离为k的指纹也就很快了。
• 总的思想:先要把检索的集合缩小,然后在小集合中检索f-d’位的海明距离
要是一时半会看不懂,那就从新回顾一下那两种极端的办法:
方法2,前61位上精确匹配,后面就不需要比较了
方法1,前0位上精确匹配,那就要在后面,也就是所有,上比较
那么折中的想法是 前d- bits相同,留下3bit在(64-d)bit小范围搜索,可行否?
d-bits的表示范围有2^d,总量N个指纹,平均 每个表示后面只有N/(2^d)个
快速定位到前缀是d的位置以后,直接比较N/(2^k)个指纹。
如此只能保证前d位精确的那部分N/(2^d)指纹没有遗漏汉明距离>3的
因此要保证64bits上所有部分都安全,全部才没有遗漏。
方法2其实就是把所有的d=61 部分(也就是64选61)都包含了。
按照例子,80亿网页有2^34个,那么理论上34位就能表示完80亿不重复的指纹。
我们假设最前的34位的表示完了80亿指纹,假设指纹在前30位是一样的,那么后面4位还可以表示24个,只需要逐一比较这16个指纹是否于待测指纹汉明距离小于3。
假设:对任意34位中的30位都可以这么做。
因此在一次完整的查找中,限定前q位精确匹配(假设这些指纹已经是q位有序的,可以采用二分查找,如果指纹量非常大,且分布均匀,甚至可以采用内插搜索),之后的2d-q个指纹剩下64-q位需要比较汉明距离小于3。
于是问题就转变为如何切割64位的q。
将64位平分成若干份,例如4份ABCD,每份16位。
假设这些指纹已经按A部分排序好了,我们先按A的16位精确匹配到一个区间,这个区间的后BCD位检查汉明距离是否小于3。
同样的假设,其次我们按B的16位精确匹配到另一个区间,这个区间的所有指纹需要在ACD位上比较汉明距离是否小于3。
同理还有C和D
所以这里我们需要将全部的指纹T复制4份,T1 T2 T3 T4, T1按A排序,T2按B排序… 4份可以并行进行查询,最后把结果合并。这样即使最坏的情况:3个位分别落在其中3个区域ABC,ACD,BCD,ABD…都不会被漏掉。
只精确匹配16位,还需要逐一比较的指纹量依然庞大,可能达到2d-16个,我们也可以精确匹配更多的。
例如:将64位平分成4份ABCD,每份16位,在BCD的48位上,我们再分成4份,WXZY,每份12位,汉明距离的3位可以散落在任意三块,那么A与WXZY任意一份合起来做精确的28位…剩下3份用来检查汉明距离。同理B,C,D也可以这样,那么T需要复制16次,ABCD与WXYZ的组合做精确匹配,每次精确匹配后还需要逐一比较的个数降低到2d-28个。不同的组合方式也就是时间和空间上的权衡。
最坏情况是其中3份可能有1位汉明距离差异为1。
算法的描述如下:
1)先复制原表T为Tt份:T1,T2,….Tt
2)每个Ti都关联一个pi和一个πi,其中pi是一个整数,πi是一个置换函数,负责把pi个bit位换到高位上。
3)应用置换函数πi到相应的Ti表上,然后对Ti进行排序
4)然后对每一个Ti和要匹配的指纹F、海明距离k做如下运算:
a) 然后使用F’的高pi位检索,找出Ti中高pi位相同的集合
b) 在检索出的集合中比较f-pi位,找出海明距离小于等于k的指纹
5)最后合并所有Ti中检索出的结果
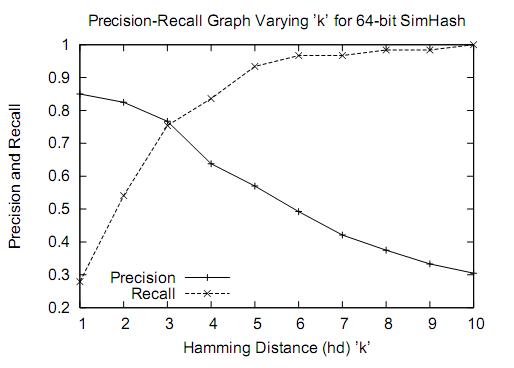
由于文本已经压缩成8个字节了,因此其实Simhash近似查重精度并不高:
最后:
翻译得有点粗,不好意思哈






















 250
250

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








