Optimum polynomial
Problem 101
If we are presented with the first k terms of a sequence it is impossible to say with certainty the value of the next term, as there are infinitely many polynomial functions that can model the sequence.
As an example, let us consider the sequence of cube numbers. This is defined by the generating function,
un = n3: 1, 8, 27, 64, 125, 216, ...
Suppose we were only given the first two terms of this sequence. Working on the principle that "simple is best" we should assume a linear relationship and predict the next term to be 15 (common difference 7). Even if we were presented with the first three terms, by the same principle of simplicity, a quadratic relationship should be assumed.
We shall define OP(k, n) to be the nth term of the optimum polynomial generating function for the first k terms of a sequence. It should be clear that OP(k, n) will accurately generate the terms of the sequence for n ≤ k, and potentially the first incorrect term (FIT) will be OP(k,k+1); in which case we shall call it a bad OP (BOP).
As a basis, if we were only given the first term of sequence, it would be most sensible to assume constancy; that is, for n ≥ 2, OP(1, n) =u1.
Hence we obtain the following OPs for the cubic sequence:
| OP(1, n) = 1 | 1, 1, 1, 1, ... |
| OP(2, n) = 7n−6 | 1, 8, 15, ... |
| OP(3, n) = 6n2−11n+6 | 1, 8, 27, 58, ... |
| OP(4, n) = n3 | 1, 8, 27, 64, 125, ... |
Clearly no BOPs exist for k ≥ 4.
By considering the sum of FITs generated by the BOPs (indicated in red above), we obtain 1 + 15 + 58 = 74.
Consider the following tenth degree polynomial generating function:
un = 1 − n + n2 − n3 + n4 − n5 + n6 − n7 + n8 − n9 + n10
Find the sum of FITs for the BOPs.
题意:
最优多项式
如果我们知道了一个数列的前k项,我们仍无法确定地给出下一项的值,因为有无穷个多项式生成函数都有可能是这个数列的模型。
例如,让我们考虑立方数的序列,它可以用如下函数生成,
un = n3: 1, 8, 27, 64, 125, 216, …
如果我们只知道数列的前两项,秉承“简单至上”的原则,我们应当假定这个数列遵循线性关系,并且预测下一项为15(公差为7)。即使我们知道了数列的前三项,根据同样的原则,我们也应当首先假定数列遵循二次函数关系。
给定数列的前k项,定义OP(k, n)是由最优多项式生成函数给出的第n项的值。显然OP(k, n)可以精确地给出n ≤ k的那些项,而可能的第一个不正确项(First Incorrect Term,简记为FIT)将会是OP(k, k+1);如果事实的确如此,我们称这个多项式为坏最优多项式(Bad OP,简记为BOP)。
在最基本的情况下,如果我们只得到了数列的第一项,我们应当假定数列为常数,也就是说,对于n ≥ 2,OP(1, n) = u1。
由此,我们得到了立方数列的最优多项式如下:
| | |
|---|---|
| OP(1, n) = 1 | 1, 1, 1, 1, … |
| OP(2, n) = 7n−6 | 1, 8, 15, … |
| OP(3, n) = 6n2−11n+6 | 1, 8, 27, 58, … |
| OP(4, n) = n3 | 1, 8, 27, 64, 125, … |
显然,当k ≥ 4时不存在坏最优多项式。
所有坏最优多项式的第一个不正确项(用红色标示的数)之和为1 + 15 + 58 = 74。
考虑下面这个十阶多项式生成函数:
求其所有坏最优多项式的第一个不正确项之和。
题解:
因为我们知道了一个数列的前k项,但我们仍无法确定地给出下一项的值,因为有无穷个多项式生成函数都有可能是这个数列的模型。从这里,我们可以想到拉格朗日插值。什么是拉格朗日插值?我简单得解释一下。
我们都做过数学的规律题,就是给你一个数列,然后让你猜下一个数是什么。这题也是这样。
先写一下拉格朗日插值的定义:
对某个多项式函数,已知有给定的k + 1个取值点:
其中 对应着自变量的位置,而
对应着自变量的位置,而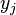 对应着函数在这个位置的取值。
对应着函数在这个位置的取值。
假设任意两个不同的xj都互不相同,那么应用拉格朗日插值公式所得到的拉格朗日插值多项式为:
其中每个 为拉格朗日基本多项式(或称插值基函数),其表达式为:
为拉格朗日基本多项式(或称插值基函数),其表达式为:
拉格朗日基本多项式 的特点是在
的特点是在 上取值为1,在其它的点
上取值为1,在其它的点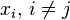 上取值为0。
上取值为0。
所谓的插值,就是“插”“值”,就是指找出一个通过给出离散数据点的函数。例如,数列中给出数据可以表示为在坐标系上的点,x坐标就是第几项,y坐标就是该项的值。然后画个图,找出这些数在哪个函数数,求出这个函数,这样就可以求出下一项了。先试一个简单的数列:1、8、27…那下一个是什么呢?
我们知道:
,
,
,
那么:
那么下一项就是将x=4代入上面的二元一次方程,就是58啦。
如果你发现这个答案其实是错的!正确的是y=x^3? 其实答案是64。那就是拉格朗日插值是错的咯?
再仔细看一下坑爹的高数课本,才发现原来是我们一直搞错了。如果我们给的是n个点,那么拉格朗日给出的函数将会是(n-1)次的。
也就是拉格朗日插值:n次多项式可以用n+1个点唯一确定.
这不坑爹吗…用公式之前还得想清楚这个函数是几次的,而且如果是更高次数的还没办法加上点去求。
这就意味着,就算是1、2、3、4、5、6…这样的数列,拉格朗日插值法在耗尽你大量的考试时间去求出通项公式以后,还会给出一个超级坑爹的答案!
那么这个方法还有什么用!
别急,前面的计算都是为后面做铺垫的。现在才是重点。
无论是分布得多么奇怪的点,拉格朗日插值法总能给出一条经过这些点的函数图象。也就是说,就算是1、2、3、4、5、6、1568这样明显不靠谱的答案也是“有规律的”。因为你总可以设一个六次多项式,找出这个数列的通项公式。
所以说:
1、3、5、7、9、1598,是对的
3、1、4、1、5、9、2、999,是对的
1,1,2,3,5,7,8989,是对的
2,4,6,8,5,是对的
你想怎么写都是对的,即使看起来不靠谱,但其仍然存在内在关系与规律。
解释完啦!
插值公式是:
拉格朗日插值法可以帮助我们解决以下的问题:
例如:已知x取值0,1,-1,2时, f{x}取值2,2,0,6 。
求x=3时f{x}的值。
#include<cstdio>
#include<iostream>
using namespace std;
int xs[4]={0,1,-1,2};
int ys[4]={2,2,0,6};
//f(3)?
int lagrange_Polynomial(int x, int xs[],int ys[])
{
int c1,c2;
int n=4;
c1=1;
for(int i=0;i<n;i++)
{
c2=ys[i];
for(int j=0;j<n;j++)
{
if(j!=i) c2=c2*((x-xs[j])*1.0)/((xs[i]-xs[j])*1.0);
}
c1+=c2;
}
return c1;
}
int main()
{
int val=lagrange_Polynomial(3,xs,ys);
cout<<val<<endl; //输出 :20
return 0;
}同理,PE101这题就可以按相同的方法解出来啦。
如果你做出了PE101,你可以做另外一题:Codeforces 622F













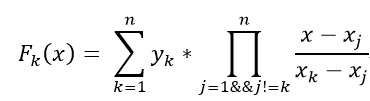














 1万+
1万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








