白话篇：零姿势实现排序二叉树的建立与查找

前篇：

二叉排序树还有很高比各的名字：二叉查找树，二叉搜索树。

为什么这么称为呢？

我们来看下二叉树的定义：

二叉排序树或者是一棵空树，或者是具有下列性质的二叉树：

（1）若左子树不空，则左子树上所有结点的值均小于它的根结点的值；

（2）若右子树不空，则右子树上所有结点的值均大于它的根结点的值；

（3）左、右子树也分别为二叉排序树；

（4）没有键值相等的结点。

思想扩展：

那么意思就是：对于一组数据，每个父节点的值小于右儿子的值，并且大于左儿子的值。满足这样要求的二叉树被称为二叉排序树。被称作二叉排序树是因为通过构造这样的一颗二叉树，它上面的每个节点（除了根节点，因为根节点没有父节点）跟父节点的值是相对有序的。

那么可以想到的是，如果我们在这颗树上，想要查找某个数据是否存在，那么我们就不必像数组那样一个个都比较，或者像二分查找那样，一次次折半比较（二分查找还要要求数据序列有序话，这无疑是很麻烦的）。

对于一颗二叉排序树来说，我们只需要比较一个数据与当前所访问的节点，根据结果去确定访问左儿子还是右儿子，这样每步的比较操作都会剪去大量的数据，无疑是很方便的进行快速的查找或者搜索。从这一点看来，二叉排序树在查找数据方面有很大的优势。这也是为什么被称作二叉查找树，二叉搜索树的原因。

中篇：

二叉排序树的建立过程模拟：

对于一组数据：

25 18 46 2 53 39 32 4 74 67 60 11

建立相应的二叉排序树

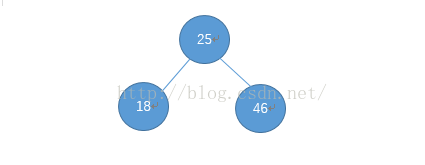
现在来看18,18小于25，存在于25 的左儿子：

现在来看46,46大于25，所以存在于25的右儿子：

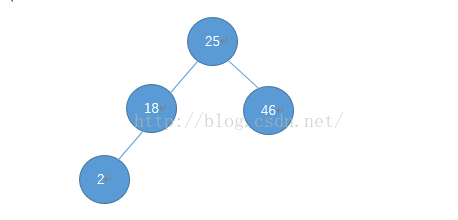
现在来看2，2小于25，查左儿子，2比18小，所以存在于18的左儿子节点：

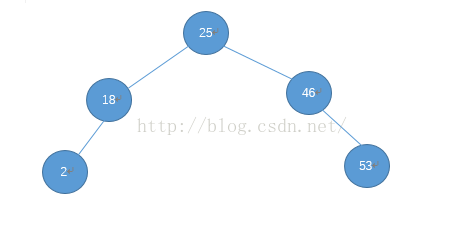
现在来看53,53大于25，查右儿子，53大于46，所以存在于46的右儿子处：

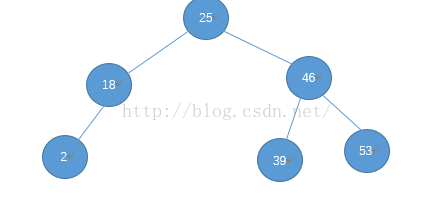
现在来看39 ， 39 大于25 ，查右儿子，39小于46 ，放在46 的左儿子处：

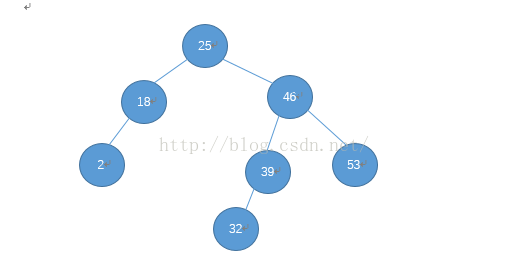
现在来看32，32大于25 ，查右儿子，32小于46，查左儿子，32小于39，放在39 的左儿子处：

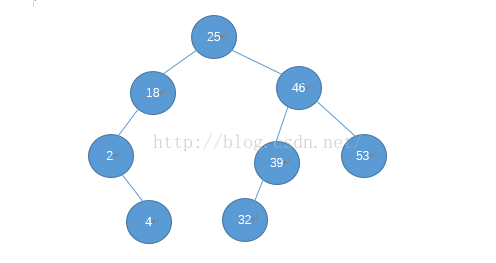
现在来看4，4 小于25 ，查左儿子，小于18 查左儿子，大于2，放在2的右儿子处：

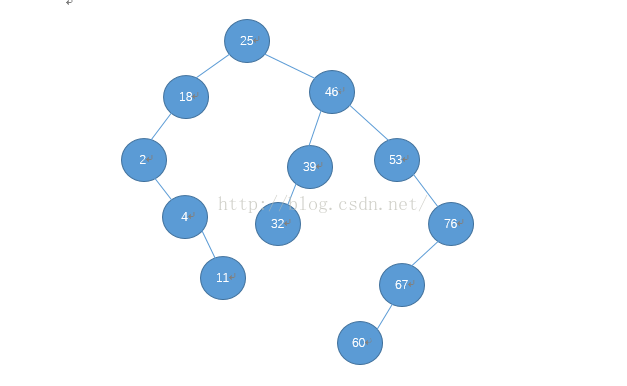
对于剩下的数据按照这种方式继续，最终得到一个二叉排序树：

由此二叉树如何查找数据呢？

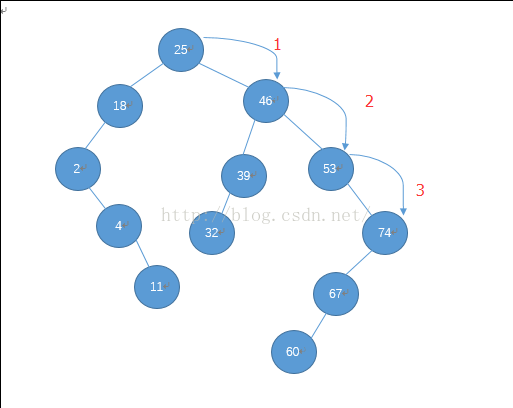
比如查找：74

过程：

74 比25大，查右儿子，74 比46 大，查右儿子，74 比53 大，查右儿子74 == 74 ，查找结束。总共比较四次。

后篇：

代码实现：

#include<stdio.h>
#include<string.h>
#include<malloc.h>
typedef struct T
{
    char data;
    struct T*l, *r;
}T;
int ans;
int pos;
bool flag = false;
void Init(T *&Tree, int e)             // 建立排序二叉树
{
    if (Tree == NULL)                    //如果当前节点为空，那么久为当前节点申请空间，并赋值为e
    {
        Tree = (T *)malloc(sizeof(T));
        Tree->data = e;
        Tree->l = Tree->r = NULL;      //赋值结束后它的子节点为空
    }
    else
    {
        if (Tree->data == e)      // 如果当前节点有值，那么就要进行比较，如果等于当前节点的值，那么就不做处理。因为二叉排序树不允许重复节点的出现
            return;
        else if (Tree->data > e)    //如果小于当前节点的值，那么肯定此数据要建立在当前节点的左节点
        {
            Init(Tree->l, e);
        }
        else if (Tree->data < e)      //如果大于当前节点的值，那么肯定此数据要建立在当前节点的右节点。
        {
            Init(Tree->r, e);
        }
    }
}
 
void Search(T *Tree,int e)        //搜索某个数据是否在当前的二叉排序树中出现
{
    if (Tree != NULL)
    {
        if (Tree->data == e)       //出现
        {
            flag = true;
            ans++;
        }
        else if (Tree->data > e)     //如果当前节点的值大于此数据，那么次数据只能出现在当前节点的左节点上
        {
            ans++;
            Search(Tree->l, e);
        }
        else if (Tree->data < e)    //如果当前节点的值小于此数据那么此数据只可能出现在当前节点的右节点上
        {
            ans++;
            Search(Tree->r, e);
        }
    }
}
int main()
{
    T *Tree;
    Tree = NULL;
    int n;
    int a[1024];
    scanf("%d", &n);
    int i;
    for (i = 0; i < n; i++)
    {
        scanf("%d", &a[i]);
        Init(Tree, a[i]);
    }
    int num;
    scanf("%d", &num);
    Search(Tree, num);
    if (flag == false)
    {
        printf("-1");
    }
    else
    {
        printf("%d", ans);
    }
    return 0;
} 

二叉排序树的特点 

由BST性质可得： 
（1） 二叉排序树中任一结点x，其左(右)子树中任一结点y(若存在)的关键字必小(大)于x的关键字。 
（2） 二叉排序树中，各结点关键字是惟一的。 
注意： 
实际应用中，不能保证被查找的数据集中各元素的关键字互不相同，所以可将二叉排序树定义中BST性质(1)里的"小于"改为"大于等于"，或将BST性质(2)里的"大于"改为"小于等于"，甚至可同时修改这两个性质。 
（3） 按中序遍历该树所得到的中序序列是一个递增有序序列。