重拾算法（一）：算法效率分析（空间复杂度和时间复杂度）

前言：

算法效率分析分为两种：第一种是时间效率，第二种是空间效率。时间效率被称为时间复杂度，而空间效率被称作空间复杂度。

时间复杂度主要衡量的是一个算法的运行速度，而空间复杂度主要衡量一个算法所需要的额外空间，在计算机发展的早期，计算机的存储容量很小。所以对空间复杂度很是在乎。但是经过计算机行业的迅速发展，计算机的存储容量已经达到了很高的程度。所以我们如今已经不需要再关注一个算法的空间复杂度。

空间复杂度：

程序所需要的空间主要由以下部分构成：
  指令空间。存储经过编译之后的程序指令。指令有操作数和操作码构成。
  数据空间。存储所有常量和所有变量值所需的空间。
  环境栈空间。保存函数调用返回时恢复运行所需要的信
息。 


（1）指令空间
程序所需指令空间的大小取决于如下因素：
  把程序编译成机器代码的编译器。所使用的编译器不同，
则产生的机器代码长度就会有所差异。
  编译时实际采用的编译器选项。 有些编译器带有选项， 如
优化模式、 覆盖模式等等。 所取的选项不同， 产生的机器
代码也会不同。
  目标计算机。 目标计算机的配置也会影响代码的规模。 例
如， 如果计算机具有浮点处理硬件， 那么， 每个浮点操作
可以转化为一条机器指令。 否则， 必须生成仿真的浮点计
算代码，使整个机器代码加长。
（2）数据空间
分成两部分：存储常量和简单变量；存储复合变量。
  存储常量和简单变量。 取决于所用的计算机和编译器， 以
及变量与常量的数目。
  存储复合变量。 包括数据结构所需的空间及动态分配的空
间。
（3）环境栈空间
调用一个函数时，下面数据保存在环境栈中：
  返回地址。
  所有局部变量的值、传值形式参数的参数值。
  所有引用参数的定义。
所以一个程序所需要的空间可分为两部分：
① 固定部分。独立于实例特征，主要包括指令空间、简单变
量以及定长复合变量占用的空间、常量占用的空间。
② 可变部分。 主要包括复合变量所需空间、 动态分配的空间、
递归栈所需要的空间。
  复合变量所需的空间依赖于所解决的具体问题。
  动态分配的空间和递归栈所需要的空间依赖于实例特征


例：template <class T> //
int Find( const T a[], int n, const T&x)
{   int i ;
for(i = 0; i<n&& a[i] != x; ++i){}
return(i== n) ? -1: i ;
} 
问题。在a[0..(n-1)]中搜索x，
若找到则回所在的位置，否
则返回-1。
  实例特征。 采用数组的长度n
作为实例特征。
  分析。数组地址a需要4字节，参数x需要4字节，n需要4
字节，局部变量i需要4字节，整数常量-1需要4字节，总
共需要20字节，独立于n，所以 ＝
Find
( ) 0 S n 。
  注意。数组a所需要的空间是在其他函数中分配的，不能
算作函数Find所需要的空间。

我们在此说明算法的时间复杂度的计算方法：
在说明之前，我先讲几个概念：

1.输入规模：

在大多数的算法中，对于输入规模较大的算法，一般运行需要的时间久更长。例如：对于一组数据进行排序，你输入 10 个数跟你输入10000个数的算法运行时间是不一样的。所以在研究算法的效率时，把它作为一个以算法输入规模n为参数的函数是非常合乎逻辑的。但是要注意的是，并不是输入了多少数据，数据规模就是多少。输入规模是需要进行选取的。比如：对于两个n*n 的矩阵，你所写的算法的输入规模可以选取为n ，也可以选取为n*n。对于大多数的情况下，选取什么作为参数都是可以看出来的（经验有了，水到渠成）。比如：对于排序，查找等算法的输入规模一般都选取它们的输入数据量n，对于n次多项式来说，它的参数就是多项式的系数。

2.算法的运行时间度量：

算法的运行时间，你第一时间看到这个可能会以为算法的运行时间肯定会以秒，分钟，甚至小时等时间的标准度来表示。但是这样的表示方式存在有很大的问题：这种方式很是依赖计算机的运行速度，依赖于算法程序实现的质量已经你选用的编译器等等。而且这种方式会导致程序的运行时间难以计算，我们必须用一种不依赖与任何无关因素的度量标准：基本操作。也被称为算法中最重要的操作。比如：对两种排序算法，我们没有办法计算出程序运行了多少时间，但是我们可以根据计算来得到每个程序的基本操作所出现的次数：加减，赋值等等。基本操作可能会有很多种，但是我们只需要找出来贡献最大的那个就行了。对于数学问题的算法：最消耗时间的是除法，其次是乘法，最后是加法和减法。

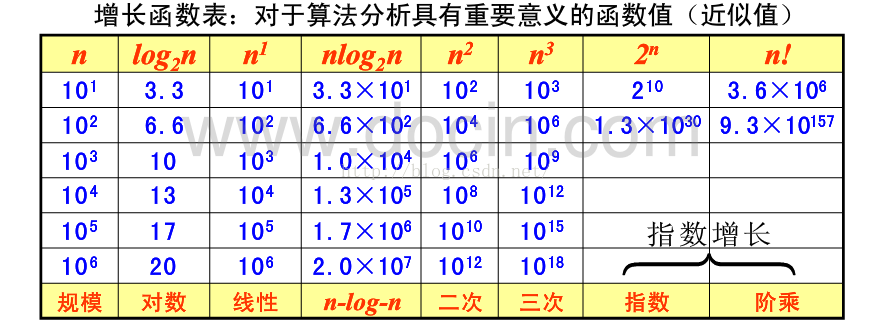
3.增长次数：

就是当n变大时，即输入规模变大时，对算法的时间复杂度相关函数的相关影响。

4.算法的平均.最差.和最优效率：

算法的最差效率：当输入规模为n时，算法在最坏情况下的效率。

算法的最优效率：当输入规模为n时，算法在最优的情况下的效率。

算法的平均效率：在实际的假设情况下，算法所可能发生的正推推断下所具有的效率。一般是通过得到或者是假设各类输入的概率分布，以推导出我们所希望                                 的基本操作次数。

以顺序查找算法为例：

算法的最差效率：n个数据，在最后一次判断才找到。效率为n。

算法的最优效率：n个数据，第一次就判断就招到，效率为1

算法的平均效率：n个数据，我们先假设能招到的概率，然后我们需要求得在第一次查找招到的概率、第二次查找招到的概率等等一直求，然后算得总的操作                                  次数。得出算法的平均效率

算法时间效率分析框架：

对于输入规模为n 的算法，我们可以统计它的基本操作执行次数，对其效率进行度量。

5.渐进符号：

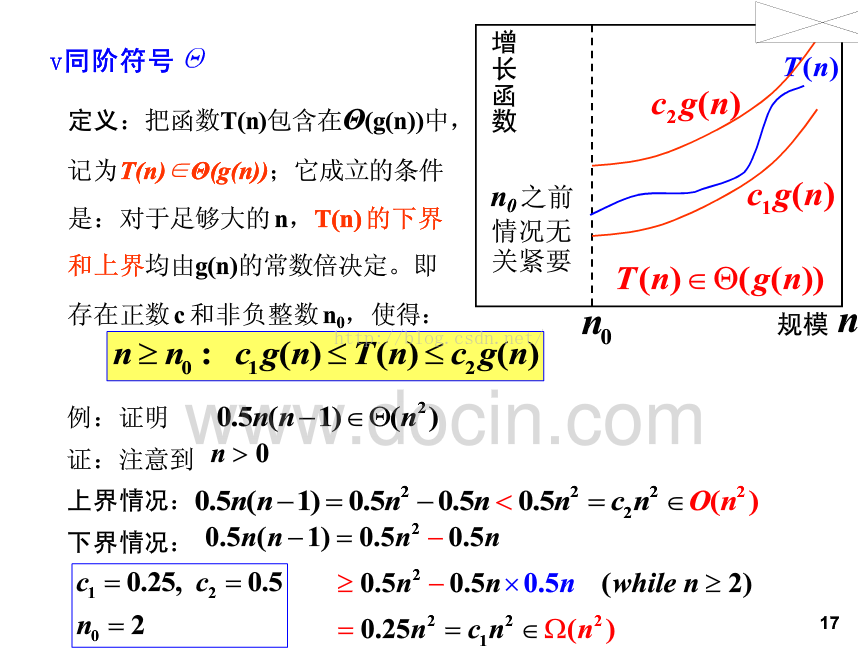
6.基本的渐进效率类型：

图片用自：

点击打开链接