接上篇,用python实现logisitic regression,代码如下:
#!/usr/bin/env python
#! -*- coding:utf-8 -*-
import matplotlib.pyplot as plt
from numpy import *
#创建数据集
def load_dataset():
n = 100
X = [[1, 0.005*xi] for xi in range(1, 100)]
Y = [2*xi[1] for xi in X]
return X, Y
def sigmoid(z):
t = exp(z)
return t/(1+t)
#让sigmodi函数向量化,可以对矩阵求函数值,矩阵in,矩阵out
sigmoid_vec = vectorize(sigmoid)
#梯度下降法求解线性回归
def grad_descent(X, Y):
X = mat(X)
Y = mat(Y)
row, col = shape(X)
alpha = 0.05
maxIter = 5000
W = ones((1, col))
V = zeros((row, row), float32)
for k in range(maxIter):
L = sigmoid_vec(W*X.transpose())
for i in range(row):
V[i, i] = L[0, i]*(L[0,i] - 1)
W = W - alpha * (Y - L)*V*X
return W
def main():
X, Y = load_dataset()
W = grad_descent(X, Y)
print "W = ", W
#绘图
x = [xi[1] for xi in X]
y = Y
plt.plot(x, y, marker="*")
xM = mat(X)
y2 = sigmoid_vec(W*xM.transpose())
y22 = [y2[0,i] for i in range(y2.shape[1]) ]
plt.plot(x, y22, marker="o")
plt.show()
if __name__ == "__main__":
main()跟前面相对,多了一点变化,sigmoid_vec是对sigmoid函数的向量化,以及计算对对 V <script type="math/tex" id="MathJax-Element-4">V</script>的计算。
我们看看计算结果:
迭代5次,拟合结果
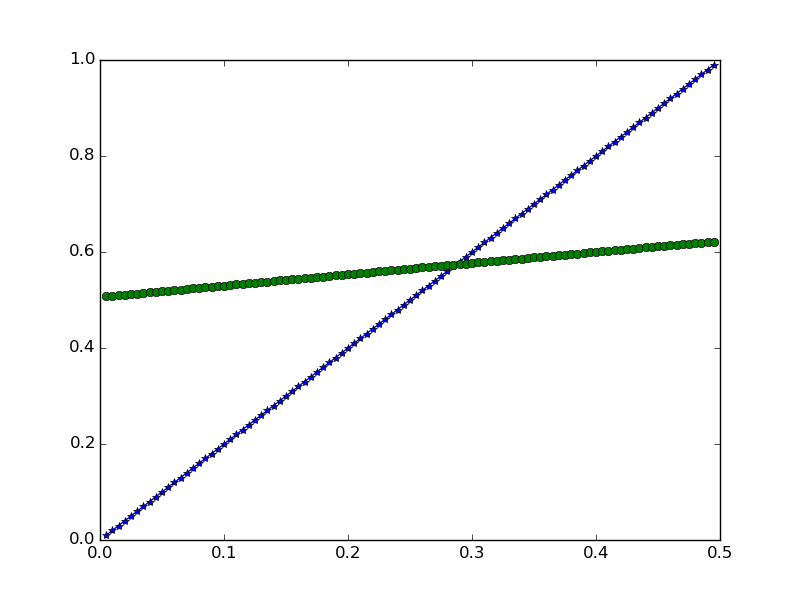
迭代50次,拟合结果
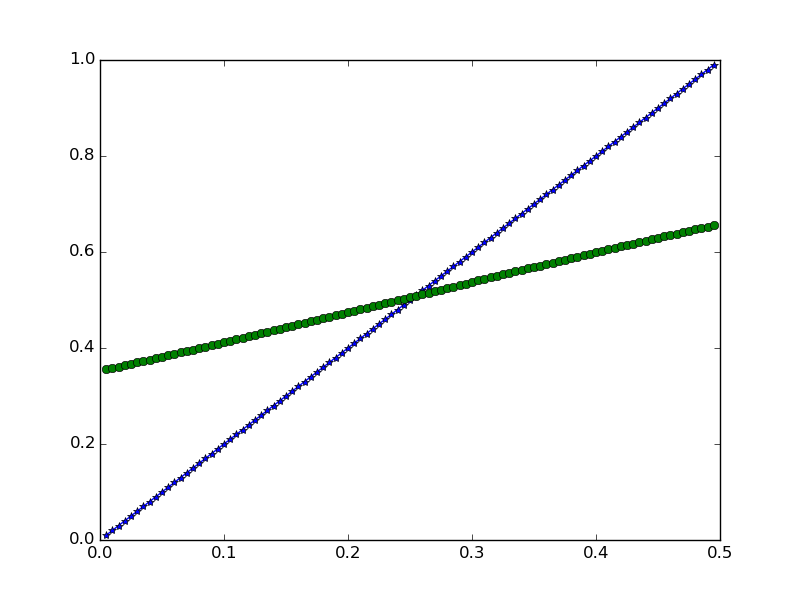
迭代500次,拟合结果
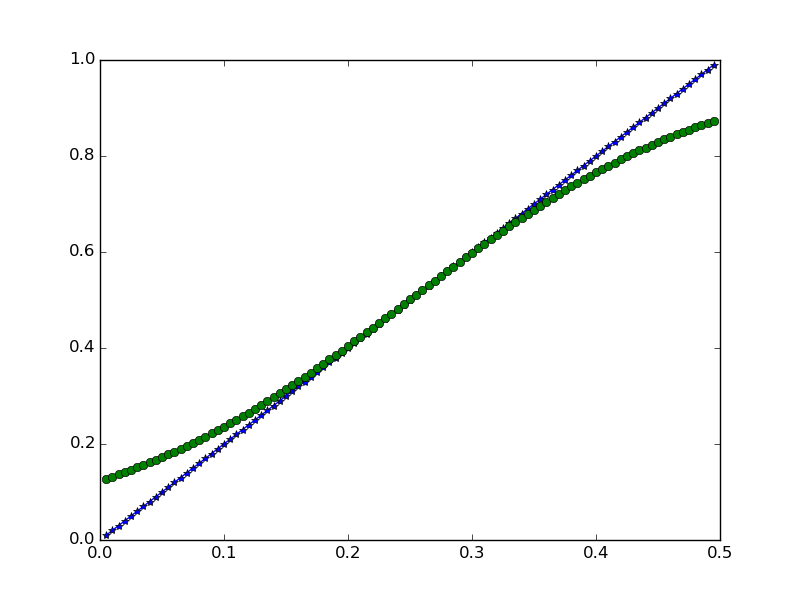
迭代5000次,拟合结果
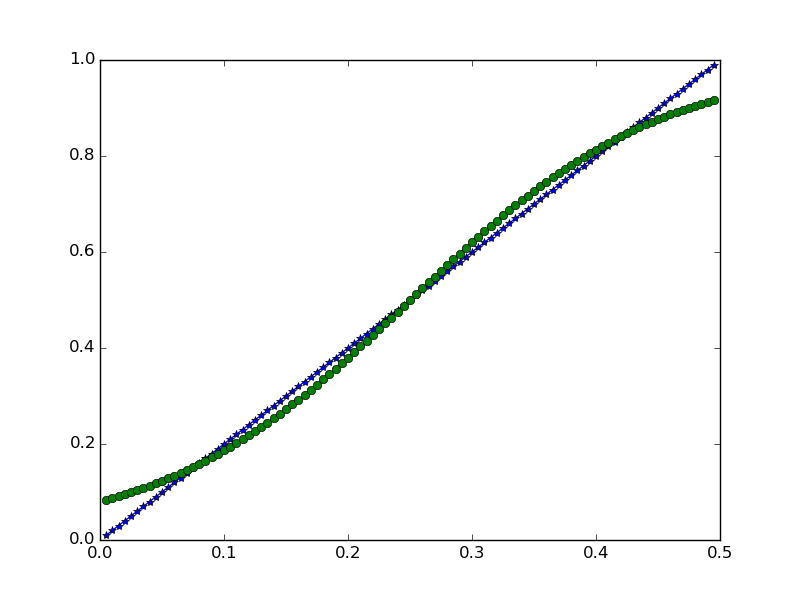
由于sigmoid函数的原因,拟合函数不是直线,这就是跟线性拟合的差别。
Logistic regression教程到此结束,就酱!






















 3359
3359

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








