http://poj.org/problem?id=1737
Description
An undirected graph is a set V of vertices and a set of E∈{V*V} edges.An undirected graph is connected if and only if for every pair (u,v) of vertices,u is reachable from v.
You are to write a program that tries to calculate the number of different connected undirected graph with n vertices.
For example,there are 4 different connected undirected graphs with 3 vertices.
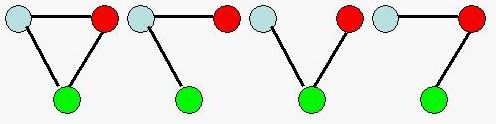
You are to write a program that tries to calculate the number of different connected undirected graph with n vertices.
For example,there are 4 different connected undirected graphs with 3 vertices.

Input
The input contains several test cases. Each test case contains an integer n, denoting the number of vertices. You may assume that 1<=n<=50. The last test case is followed by one zero.
Output
For each test case output the answer on a single line.
Sample Input
1 2 3 4 0
Sample Output
1 1 4 38
/**
poj1737 组合dp
题目大意:给定节点数n,问由这些节点组成的连通图有多少种
解题思路:从n个点所有的连接方法中删去那些不能构成连通图的连法.然后想法就是用f[i]记录i个点的连通图数目,然后递推.
具体来说,为了避免重复,选择一个固定点x,不管怎样,我们先选择x这个点,然后再从其他剩余的n-1个点中
分别选0~n-2个点与x构成连通图.然后其他剩余的n-1~1个点他们之间的连接方法随意,也就是2^m种.
m=完全图的边数=点数*(点数-1)/2.
初值f[1]=1最后的公式也就是:
f[n]=2^(n*(n-1)/2)-(f[1]*c[n-1][0]*2^((n-1)*(n-2)/2)+...+f[i]*c[n-1][i-1]*2^((n-i)*(n-i-1)/2+...+f[n-1]*c[n-1][n-2]*2^0)
*/
import java.math.*;
import java.util.*;
public class Main {
public static void main(String[] args) {
BigInteger two[] = new BigInteger [2556];
two[0] = BigInteger.ONE;
for(int i = 1; i <= 2550; i++)
two[i] = two[i - 1].multiply(BigInteger.valueOf(2));
BigInteger h[] = new BigInteger [55];
for(int i = 1; i <= 50; i++){
h[i] =two[(i*(i-1))/2];
}
BigInteger C[][] = new BigInteger[55][55];
C[0][0] = BigInteger.ONE;
for(int i = 0; i <= 50; i++){
C[i][0] = C[i][i] = BigInteger.ONE;
for(int j = 1; j < i; j++){
C[i][j] = C[i - 1][j].add(C[i - 1][j - 1]);
}
}
BigInteger f[] = new BigInteger[55];
BigInteger g[] = new BigInteger[55];
f[1] = BigInteger.ONE;
for(int i = 2; i <= 50; i++) {
g[i] = BigInteger.ZERO;
for(int j = 1; j < i; j++) {
g[i] = g[i].add(C[i - 1][j - 1].multiply(f[j]).multiply(h[i - j]));
}
f[i] = h[i].subtract(g[i]);
}
int n;
Scanner cin = new Scanner(System.in);
while(cin.hasNext()){
n = cin.nextInt();
if(n == 0) break;
System.out.println(f[n]);
}
}
} 





















 352
352

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








