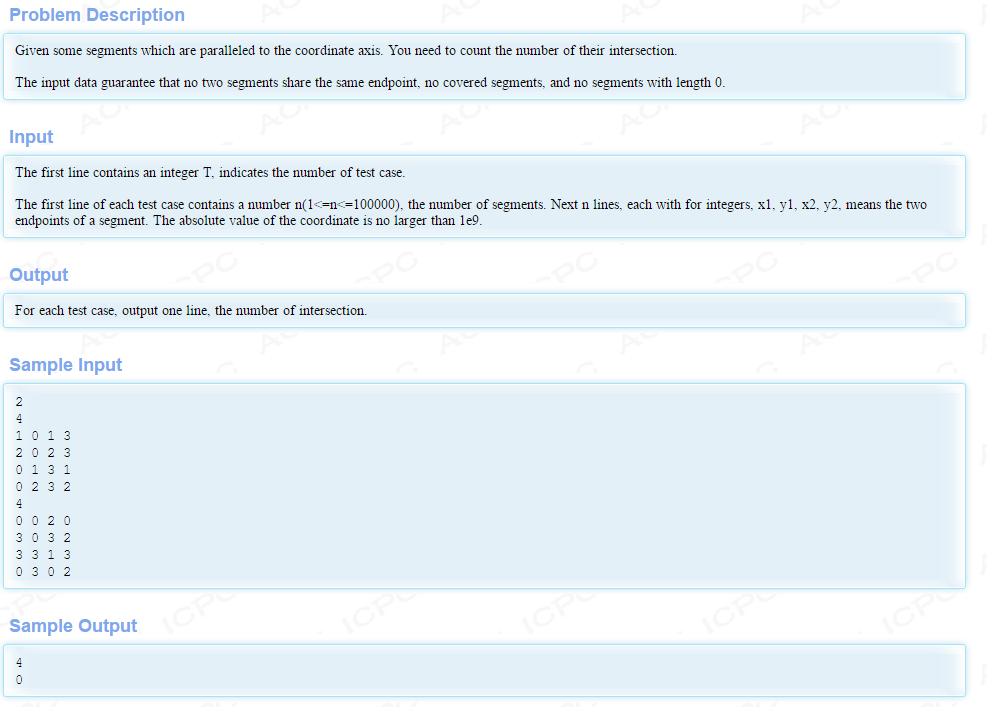
Counting Intersections

Counting Intersections

.
.
题意：给出平行于坐标轴的线段，保证无重叠，端点相同的情况，问有多少交点。
.
.
解法：首先我把数离散化，那么数的大小不超过4*10^5，这样就可以用树状数组。首先把平行于x、y轴的分开存。对于垂直于x轴的按x坐标排序，对于垂直于y轴的按x坐标左端点进行排序。然后扫描垂直x坐标轴的线段，可以很快找到所以垂直y轴的而且左端点在该x坐标左边的所有线段（显然这个扫描是线性的），我把这些线段放到堆中维护（代码中用了heap），以右端点为关键字，那么可以很快剔除所有右端点在x坐标左边的、即不合法没有与这条线段相交的线段（同样是线性的），于是我们得到了所有垂直y轴而且横跨过该x坐标的所有线段，用树状数组维护就好了。
.
.

#include <iostream>
#include <stdlib.h>
#include <stdio.h>
#include <algorithm>
#include <map>
#include <string.h>
using namespace std;

const int maxn = 200010;

int input[maxn][5], num, tot, tot_x, tot_y, n, t;
long long ans, f[4*maxn];

struct Node{
    int num, x, y;
    bool operator<(Node &other) {
        return num < other.num;
    }
}to_sort[4*maxn];

struct dy {
    int y, x1, x2;
    bool operator<(const dy &other) const {
        if (x2 == other.x2)
        {
            if (x1 == other.x1)
            {
                return y < other.y;
            }
            return x1 < other.x1;
        }
        return x2 < other.x2;
    }
}y_a[maxn];

bool cmp(dy t1, dy t2) {
    return t1.x1 < t2.x1;
}

struct dx {
    int x, y1, y2;
    bool operator<(const dx &other)const {
        return x < other.x;
    }
}x_a[maxn];

map<dy, int> heap;

void insert(int x) {
    while (1) {
        f[x] = f[x] + 1ll;
        x = x+(x & (-x));
        if (x > num) break;
    }
}

void cancel(int x) {
    while (1) {
        f[x] = f[x] - 1ll;
        x = x+(x & (-x));
        if (x > num) break;
    }
}

long long find(int x) {
    long long sum = 0;
    while (1) {
        if (x == 0) break;
        sum = sum+f[x];
        x = x-(x & (-x));
    }
    return sum;
}


int main() {

    int tt;
    scanf("%d", &tt);
    while (tt--) {
        tot = 0;
        scanf("%d", &n);
        for (int i = 1; i <= n; i++)
            for (int j = 1; j <= 4; j++) {
                tot++;
                scanf("%d", &to_sort[tot].num);
                to_sort[tot].x = i;
                to_sort[tot].y = j;
            }
        sort(to_sort+1, to_sort+tot+1);
        num = 1;
        input[to_sort[1].x][to_sort[1].y] = num;
        for (int i = 2; i <= n*4; i++) {
            if (to_sort[i].num != to_sort[i-1].num) num++;
            input[to_sort[i].x][to_sort[i].y] = num;
        }
        tot_x = 0;
        tot_y = 0;
        for (int i = 1; i <= n; i++) {
            if (input[i][1] == input[i][3]) {
                tot_x++;
                x_a[tot_x].x = input[i][1];
                x_a[tot_x].y1 = min(input[i][2], input[i][4]);
                x_a[tot_x].y2 = max(input[i][2], input[i][4]);
            } else if (input[i][2] == input[i][4]) {
                tot_y++;
                y_a[tot_y].y = input[i][2];
                y_a[tot_y].x1 = min(input[i][1], input[i][3]);
                y_a[tot_y].x2 = max(input[i][1], input[i][3]);
            }
        }
        sort(x_a+1, x_a+tot_x+1);
        sort(y_a+1, y_a+tot_y+1, cmp);
        if (tot_x+tot_y != n) while (1) {}
        heap.clear();
        memset(f, 0, sizeof(f));
        t = 1;
        ans = 0;
        for (int i = 1; i <= tot_x; i++) {
            while (t <= tot_y && y_a[t].x1 <= x_a[i].x) {
                heap[y_a[t]] = 1;
                insert(y_a[t].y);
                t++;
            }
            while (1) {
                if (heap.size() == 0) break;
                map<dy, int>::iterator k = heap.begin();
                if (k->first.x2 < x_a[i].x) {
                    cancel(k->first.y);
                    heap.erase(k);
                } else break;
            }
            ans = ans+find(x_a[i].y2)-find(x_a[i].y1-1);
        }
        printf("%lld\n", ans);
    }

}