动态规划问题详解(三)

   在动态规划问题详解1,2中，我们只是拿了2个例子说明了一下什么是动态规划，及解题的思路。并没有形成一套完整的理论。这篇文章，我们将讨论如何用数学模型给动态规划问题建模。

                                                                                                               图一

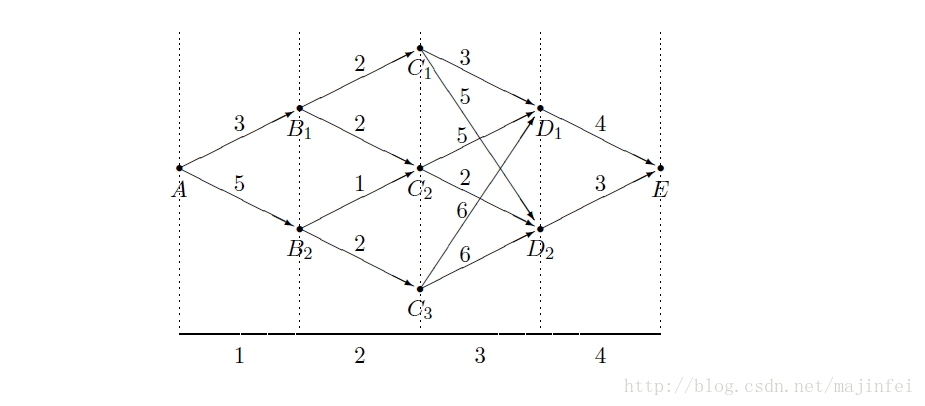
    如图一所示，找出从A--->E 点的最短路径。

 阶段变量

   我们把整个过程分成4个阶段，A->B1(B2) , B1(B2)-->C1(C2,C3) , C1(C2,C3)->D1(D2), D1(D2)->E.整个问题，可以看成是4个阶段的决策问题，描述阶段次序的变量，称为阶段变量。用k来表示。

状态

 一个阶段在开始时所面临的状况，称为状态，一个状态，既是起点，又是终点。每个阶段的所有的状态，构成了状态集合。如第一阶段的状态的集合为{A}，第三阶段的状态的集合为{C1,C2,C3,C4}.描述过程状态的变量，称为状态变量。一般用x_k来表示第k个阶段的某个状态.

决策

  一个阶段的状态给定以后，从一个状态到另一个状态的选择，我们称之为决策。用来描述这种选择的变量称为决策变量，一般用u_k(x_k)表示第k个阶段，状态为x_k的决策变量。决策变量，允许选择的变量，称为允许决策变量用U_k表示。如果用X_3表示第三个阶段的状态的集合，则X_3={C1,C2,C3} .如果从C2出发，则U_2(c2)={D1,D2}如果我们选择了D2，那么u_3(c2)=D2

策略

由各个阶段的决策，u_k(x_k)  k={1,2,3,....n}组成的决策序列，称为一个策略，一般用P表示一个策略。P_n={u_1(x_1),u_2(x_2)....u_n(x_n)}

在实际的问题中，可供选择的策略是有限的，如{A,B2,C3,D2,E}.  是一种策略。图1中所示的，允许策略集合一共包含2*2*2*1=8个策略。允许策略集合中达到最优效果和策略称为最优策略。

状态转移方程

所谓状态转移就是过程由于一个状态转变到另一个状态的变化。显然，它既与前一状态有关，又与所选择的决策有关。显然，第k段的状态x_k和决策u_k(x_k)一经确定后，第k+1段的状态x_k+1,也就随之确定。那么这个对应关系可记作：

x_k+1=T_k(x_k,u_k(x_k))称为由状态x_k到x_k+1状态转移方程。在图1中，当x2=B1,时，u_2(x2)=C2,则有下一个状态 c2= T(B1,C2)

指标函数

为了衡量策略的优劣，我们引入了指标函数，用V_kn表示。最优指标函数胜f_k_n表示。图1 中，f_k_n表示从点xk到终点的最短路径。

基本思想

 

我们仍然以图1为例。我们假设在A-E的最短路径中，存在一点p,则P->E是最短的路径。有了以上的思想之后，我们就可以采用逆序求解的思想进行了。

逆序求解

   如图1中，我们可以先求解第四阶段的最优解。然后再求第三阶段，第二阶段，第一阶段。

当k=4时，f_4(D1)=4

当k=3时，出发点有c1,c2,c3 .

f_3(c1)=d(C1,D1)+ f_4(D1))= 7   当C1选择D1时

f_3(c1)=d(C1,D2)+f_4(D2)=8 当C1选择D2时。

最f_3(c1)的最小值7，则第三阶段的最优解为f_3(c1)=7，其策略为u_3(c1)=D1

直到求出f1.

 

 

因为是倒序，所以k的状态由k+1的状态及策略决定。