将 线性回归 ,logistic 回归 用在 分类 上面
我们回顾一下上节所学习的内容。总共学习了三种线性模型(线性分类,线性回归,logistic 回归),他们的核心都是
他们三种情况分别为
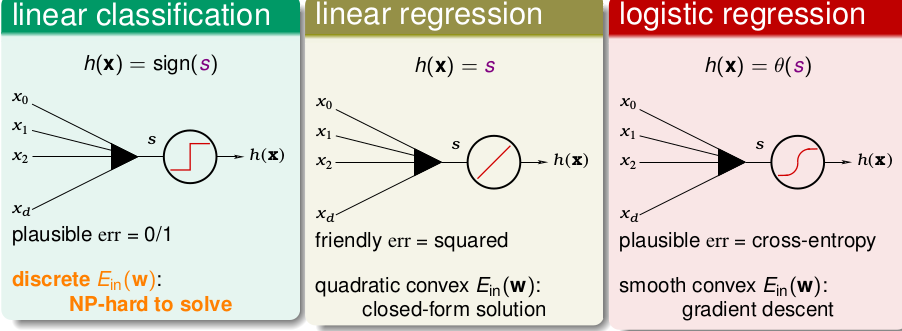
那么问题是,能否将线性回归,logistic 回归 运用到 线性分类 呢??
其实,分类是一种特殊的回归,只是输出的结果y仅仅为{-1,1}罢了!
分类问题,对于某一个样本,其y仅为-1或者1。该样本的误差为err(s,y) 。注意:不是
Ein
,err(s,y)表示某一个样本的误差,而
Ein
表示的是将所有样本的err(s,y)相加的和再除以N,得到的平均值。
那么三种模型的err(s,y)分别为

注意:由于是分类问题,那么上图的y只能为1或者-1。但是s的值就不是仅仅只有1或者-1了。
那求得的三种模型的err(s,y)就分别为

0/1表示 线性分类的。 sqr表示线性回归的。ce表示logistic回归的。
以ys为横坐标,err值为纵坐标。则可汇出图形为
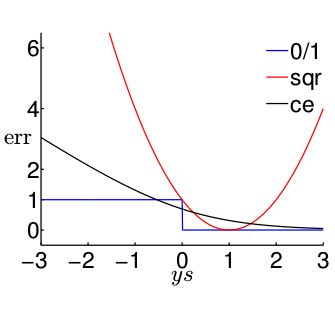
我们来看看ys的物理意义。y是样本的标签,s是模型对这个样本预测的值,s=
wTx
为实数,无穷多个取值。如果y=1,那么我们肯定希望s>0,如果y=-1,那么我们肯定希望s<0。所以,ys>0表示 模型分类正确,ys<0表示模型分类错误。
1. 我们来看看0/1模型的情况,ys>0,err=0;ys<0,err=1.
2. 但是,我们看sqr模型就不一样了。ys<<1,err很大,(哎,大就大呗,反正ys<0,是应该受点惩罚,只是这惩罚有点大)。但是当ys>>1,时,为什么sqr模型的err却依然那么大啊!!!ys>>1,表示的是模型分类是正确,err为0 才对,为什么还越来越大。所以,只有使得sqr的err很小时,此时的sqr才会和0/1的err相接近,才会一样小。所以我们是sqr的err小的话,可以使得0/1的err也小;但是0/1的err小,并不代表sqr的err小。
3. 再看ce模型。很显然,ce的err小的话,0/1的err也小;0/1的err小的话(不管怎么小,都为0),ce 也小。
为了方便,我们对ce err的表达式除了
ln2
,可以使得图型的ys为0是,err为1。
得到图形为
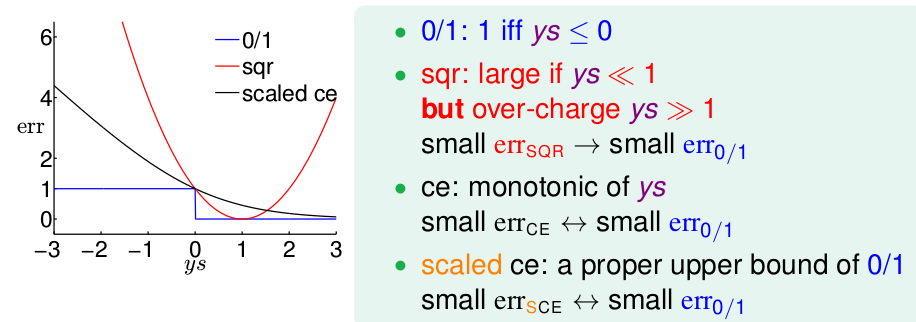
这样曲线恒再0/1曲线的上方。err是一个样本的误差,
Ein
是把所有的err求和去平均就有
对0/1和ce模型分别用之前讨论的VC bound
Eout<=Ein+...‾‾‾√
即
即可知,只要我们保证 ce
Ein
足够小,就可以保证0/1分类的
Ein
小。同理 只要我们保证 linear regression
Ein
足够小,就可以保证0/1分类的
Ein
小。
所以可以将线性回归和逻辑回归用再分类上面。
方法就是,我们用线性回归或逻辑回归用分类的样本(y={-1,1})求出权重w,再得到
sign(wx)
即可.
即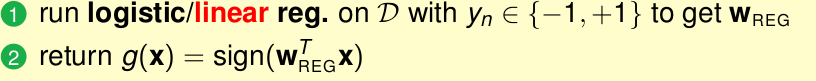
PLA,linear regression , logistic regression 进行classification的优缺点

一般的,我们用 linear regression为PLA/pocket/logistic 设定初始化值
w0
.
一般不用pocket,用logistic取代他。
随机梯度法 SGD
我们回顾以前讲的内容,发现 总共学习了两种迭代优化的方法–PLA和logistic 回归
这两种方法的核心为
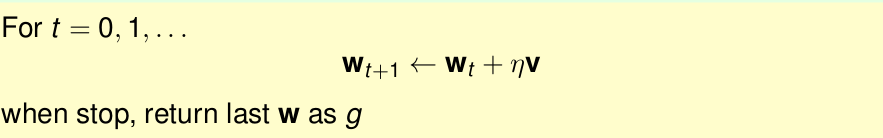
PLA的思想是,每次迭代我只取出一个样本,进行处理。即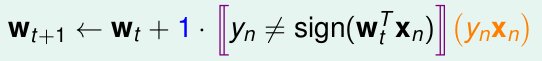
而logistic 回归的思想是,每次迭代取出所有的样本来求出梯度值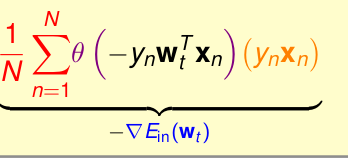
所以,我们能否也让logisitc 回归每次迭代的复杂度为O(1)呢?
我们以前用logistic回归的公式为
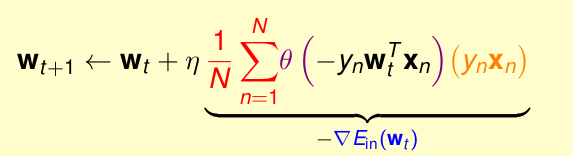
这是我们用梯度下降法得到的,他的
Ein
是沿着梯度的方向向下走的。那么为了能让复杂度为O(1),我们不强求下降方向一定要是梯度,也就是大概梯度方向就行。即

那怎样做到这一点呢???
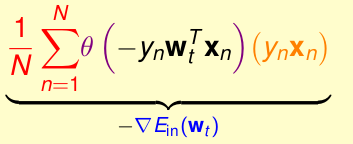
其实我们可以把上图看成是,期望值(也就是均值)。你有10000个数字,求他们的期望,由于太复杂,我就随机抽取几个点去求这几个点的期望。这就好比我们现在的随机梯度法,只是随机梯度法随机仅仅抽取的1个点,求这一个点的期望(就是他本身)。我们就用这一个点的期望去替代总体样本的期望。这就把原始的梯度下降法改成了我们现在的随机梯度法。
所以运用随机梯度法替代原来的梯度下降法,最终得到的公式为
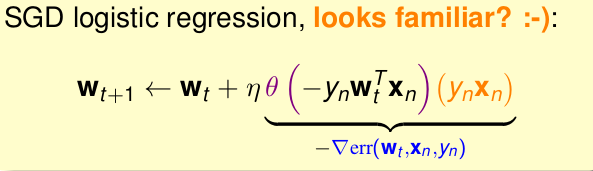
优点:快,运输量低,适于大数据,适于在线学习online learning
缺点:稳定性会降低,
由于无法达到最低,所以停止条件是:循环足够多次
一般取
η
为0.1(个人习惯,和个人经验)
SGD logistic回归与PLA的关系
用logistic回归做多分类问题
现在我们想分类成为下图的样本进行分类

方法一:
我们用二分类的分类器帮助我们进行多分类

思想:我们每次抽取一个类别比如“方块”,将其作为“o”,其他的所有的类别作为“×”,依次这样,我们可以做出4个分类器。
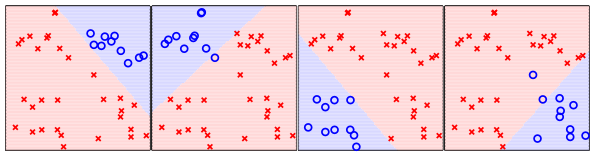
以上4个分类器依次对方块,菱形,三角,五角星 分类。
现在,我有一个新样本,他位于方框的右上角。很显然,第一个分类器说是“o”,而其他的分类器几乎都说是”×”,那么我们就可以说这个新样本的类别就是“方框”。也就是说,以后来的新样本,一般(仅一般情况)有一个分类器说是“o”,其他三个说是“×”。那么就可以说这个样本属于这个说“o”的分类器对应的标签 了。
但是存在一个很大的问题

就是在上图中的正中心,每个分类器都会说是“×”,在正中心的正上,正下,正左,正右,四个小块都会有两个分类器说是“o”。
所以,这种用二分类,结果仅能是“×”或者“o”的方法,存在不可解的情况。
那么我们就不那么绝对,一定要是“×”或者“o”。我们用概率的形式来做。
现在就来介绍,这一部分的主人公:
多分类之logistic回归 OVA(1对多 one versus all)
该方法与上面的思路基本相同。也是对每个类别和其他所有的类做分类器,所以也是做4个分类器。不同之处是,每一个小 分类器的输出,不在是绝对的“o”或者“×”,而是属于“o”的概率。假如我有一个样本,把他带入4个分类器,计算出该样本在每一个分类器上面属于“o”的概率值,取出概率值最大的那个分类器,该分类器对应的类别就是新样本的类别。
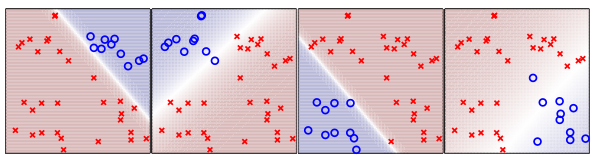
上面四个分类器,把新样本带入4个分类器,计算出该样本在每一个分类器上面属于“o”的概率值,取出概率值最大的那个分类器,该分类器对应的类别就是新样本的类别。
即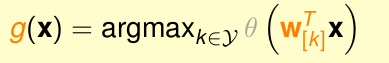
算法总结为:
1. 对于k个类别,循环k次
第i次,取出第i个类作为“o”,其他所有类(k-1个)都作为“×”,用logistic 回归训练概率模型(输出结果为 属于“o”的概率)
循环k次,则有k个logistic模型
2. 把新样本依次带入k个分类器,计算出该样本在每一个分类器上面的输出(属于“o”的概率值),输出值(属于”o”概率值)最大的那个分类器对应的类别就是新样本的类别。
即
优点:效率高,用的是logistic回归
缺点:当k很大,每个类对应的样本数相对于N就会很小,那么就会很不稳定。原因:见下:(但这依然是个很好的方法,在k不大的情况下)
一对多有个问题
当你的类别k很大的时候,即每个类别样本的数量相对于N都很小,那么每个类别的分类器都会努力的去猜‘×’。假如N=100,你的类别K=100,那么对于每一个类别分类器,都是,仅有一个样本为“o”,其他99个都是”×”。也就是说模型都会去猜“×”,那么每个小模型都有99%的正确率。那么你的最终模型就是在一堆都爱猜“×”的模型里选一个最大的类别。很显然,这样结果就会不稳定,并不是很好,并且你还会以为很好。
用线性分类投票法做多分类问题 (1对1 )(one versus one)
上面的算法是对于K个类别,每次选取1个类别作为“o”,其他所有的类别作为“×”,所以叫 1对多(one versus all)。总共循环k次。
而这次这个算法,每次选取1个作为“o”,再选一个类别作为“×”,用这两个类的数据训练小模型,所以称为 1对1(one versus one)。总共循环
C2k
次。共
C2k
个模型。
比如有4个类,k=4,那么总共有
C24
=6个模型,如下图


假设有一个新样本,假设他位于右上角,我们把他依次放在这6个模型中。那么第一个模型输出结果为“方块”,第二个模型输出结果为“方块”,第三个模型输出结果为“方块”,第四个模型输出结果为“菱形”,第五个模型输出结果为“五角星”,第六个模型输出结果为“五角星”。那么经过投票,得到最终这个新样本的类别为“方块”。
算法总结:
1. 有k个类别,那么我们循环
C2k
次
对于第i次循环,取出一个类别数据作为“o”,再取出一个类别数据作为“×”,用linear classfication 训练小模型。
所以总共有
C2k
次
2. 把新样本依次投入
C2k
个小模型里,运用投票的方法,选出k个类别中获得票数最佳的类别作为新样本的类标签。

优缺点:









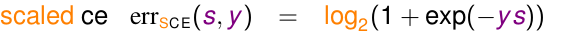


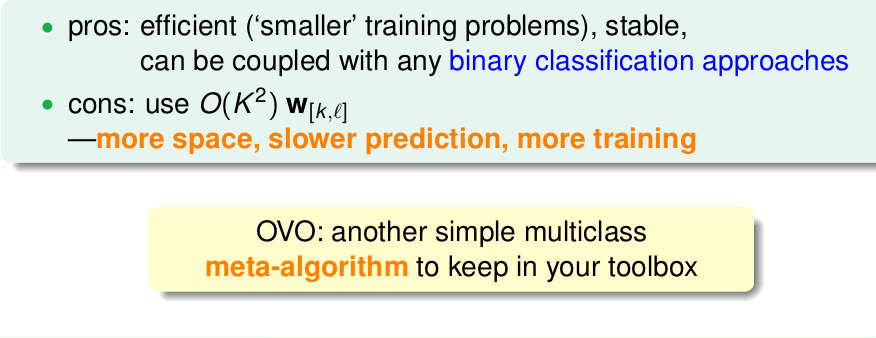
















 7335
7335

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








