(一)最长公共子序列
问题描述:给定一个序列  , 序列
, 序列 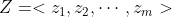 称为 X 的子序列,当存在一个严格递增的X的下标序列
称为 X 的子序列,当存在一个严格递增的X的下标序列 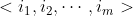 ,对所有的
,对所有的  ,都有
,都有 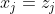 。求两个序列的长度最长的公共子序列的问题就被称为最长公共子序列问题(Longest-common-subsequence problem, LCS)。
。求两个序列的长度最长的公共子序列的问题就被称为最长公共子序列问题(Longest-common-subsequence problem, LCS)。
注意,在这个问题中,子序列中的元素不一定在原序列中是相邻的。
这是经典的动态规划问题,具体的分析过程,许多算法书上都讲过了,可以参考《算法导论》第十五章。下面两张图片取自《算法导论》第十五章,描述的是该问题的转移方程及及动态生成最优解的过程。
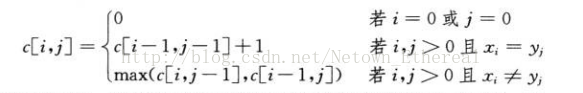
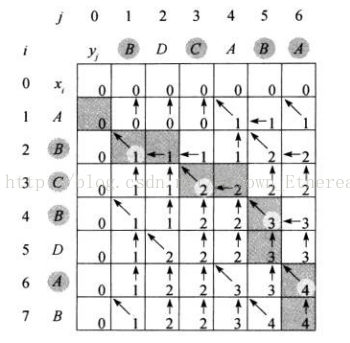
下面是针对HDU 1159 问题的我的AC代码:
//hdj1159
//dynamic programing, LCS
#include <iostream>
#include <string>
using namespace std;
int LCS(string s1, string s2)
{
int len1 = s1.length();
int len2 = s2.length();
int** a = new int*[len1 + 1];
int i, j;
for(i = 0 ; i < len1+1 ; i++) a[i] = new int[len2+1];
for(i = 0 ; i < len1+1 ; i++) a[i][0] = 0;
for(j = 0 ; j < len2+1 ; j++) a[0][j] = 0;
for(i = 1 ; i < len1+1 ; i++)
{
for(j = 1 ; j < len2+1; j++)
{
if(s1[i-1] == s2[j-1]) a[i][j] = a[i-1][j-1]+1;
else if( a[i-1][j] > a[i][j-1] ) a[i][j] = a[i-1][j];
else a[i][j] = a[i][j-1];
}
}
return a[len1][len2];
}
int main()
{
string s1, s2;
while(cin>>s1>>s2)
{
cout<<LCS(s1, s2)<<endl;
}
return 0;
}(二)带权值的最长公共子序列
问题描述,HDU 1080 , 给定两个由指定字母组成的字符串,可以在两个字符串的任意位置添加任意的字符 ‘-’ ,现在要求将两个字符串进行配对,同时,任意两个字符之间配对都有一个权值,要求使得总权值最大的匹配。
假设原字符串是 , 设
表示
的前缀子串
与
的前缀子串
之间的最大匹配值。则
的生成有三种情况:
(1)在 的位置插入字符 ‘-’ 。此时,
;
(2)在 的位置插入字符 ‘-’ 。此时,
;
(3)直接令 与
进行匹配。 此时,
;
当然, 取三者中的最大者,因此有以下转移方程:
根据转移方程,不难给出该问题的解答。以下是我的AC的代码:
//hdj1180
//dynamic programing, LCS with weight
//
#include <iostream>
#include <string>
#define Inf 999999
using namespace std;
int weight[5][5]={
5, -1, -2, -1, -3,
-1, 5, -3, -2, -4,
-2, -3, 5, -2, -2,
-1, -2, -2, 5, -1,
-3, -4, -2, -1, -Inf
};
int findindex(char ch)
{
if(ch == 'A') return 0;
else if(ch == 'C') return 1;
else if(ch == 'G') return 2;
else return 3;
}
int max(int a, int b, int c)
{
return a>b?a>c?a:c:b>c?b:c;
}
int LCS(string s1, int len1, string s2, int len2)
{
int** a = new int*[len1 + 1];
int i, j;
for(i = 0 ; i < len1+1 ; i++) a[i] = new int[len2+1];
a[0][0] = 0;
for(i = 1 ; i < len1+1 ; i++) a[i][0] = a[i-1][0] + weight[4][findindex(s1[i-1])];
for(j = 1 ; j < len2+1 ; j++) a[0][j] = a[0][j-1] + weight[findindex(s2[j-1])][4];
for(i = 1 ; i < len1+1 ; i++)
{
for(j = 1 ; j < len2+1; j++)
{
int tmp1 = a[i-1][j-1] +weight[findindex(s1[i-1])][findindex(s2[j-1])];
int up = a[i-1][j] + weight[findindex(s1[i-1])][4];
int left = a[i][j-1] + weight[4][findindex(s2[j-1])];
a[i][j] = max(tmp1, up, left);
}
}
return a[len1][len2];
}
int main()
{
int T;
cin>>T;
while(T--)
{
string s1, s2;
int len1, len2;
cin>>len1>>s1;
cin>>len2>>s2;
cout<<LCS(s1, len1, s2,len2)<<endl;
}
return 0;
}(三)最长递增子序列
问题描述,求一个给定序列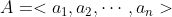 中最长的递增子序列的长度。
中最长的递增子序列的长度。
方法1:排序+LCS
一个简单的思路是将给定的序列先进行有序化( O(nlog(n))),然后使用LCS算法来查找给定的序列及有序化后的序列之间的最长公共子串(O(n2))。这个方法显然不够好。
方法2:DP
为了有效的使用DP算法,我们先要描述该问题的最优子结构性质。设 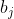 表示 A的前缀子序列
表示 A的前缀子序列  的最长递增子序列的长度。现在考虑
的最长递增子序列的长度。现在考虑  的值。对于
的值。对于 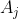 的任意一个长度为
的任意一个长度为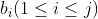 的递增子序列,如果
的递增子序列,如果  能够添加到该序列的末尾构成一个新的递增子序列,那么
能够添加到该序列的末尾构成一个新的递增子序列,那么  。显然,枚举所有这样的
。显然,枚举所有这样的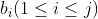 ,将得到不同的
,将得到不同的 , 取其最大者则得 最终的
, 取其最大者则得 最终的 。即有如下转移方程:
。即有如下转移方程:
显然这是可以用动态规划从左往右计算的。算法的实现代码如下;
int a[MAXN];
int LIS_DP(int n)
{
int * lenth = new int[n];
int i;
for(i=0;i<n;i++)
{
lenth[i] = 1;
for(int j=0;j<i;j++)
if( a[j] < a[i] && lenth[j]+1 > lenth[i]) lenth[i] = lenth[j]+1;
}
int max = lenth[0];
for(i = 1 ; i < n ; i++)
if(lenth[i] > max) max = lenth[i];
delete [] lenth;
return max;
}这个算法的时间复杂度是
方法3:更有效的DP算法
观察原转移方程  , 可以发现,
, 可以发现, 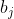 存储的是
存储的是  的最长递增子序列的长度,而
的最长递增子序列的长度,而  的最长递增子序列不一定是以
的最长递增子序列不一定是以 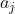 结尾的。但,我们在计算
结尾的。但,我们在计算  的时候却依然要将 每一个
的时候却依然要将 每一个 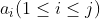 与
与 进行比较,因为我们并不知道长度为
进行比较,因为我们并不知道长度为 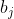 的递增子序列的结尾元素最小是多少,因此也就不能判断是否能将
的递增子序列的结尾元素最小是多少,因此也就不能判断是否能将 添加到长度为
添加到长度为 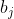 的递增子序列的末尾。这样做是很浪费时间的,因为每次要确定
的递增子序列的末尾。这样做是很浪费时间的,因为每次要确定  是否能添加到
是否能添加到 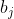 末尾时,都要从头进行一次比较,而这里面大多数次的比较在确定
末尾时,都要从头进行一次比较,而这里面大多数次的比较在确定  是否能添加到
是否能添加到  末尾时就已经进行过了。那么,我们为什么不将 长度为
末尾时就已经进行过了。那么,我们为什么不将 长度为 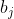 的递增子序列的最小末尾元素储存起来,便于下次直接确定
的递增子序列的最小末尾元素储存起来,便于下次直接确定  是否能插到该序列末尾呢?
是否能插到该序列末尾呢?
由此,我们可以重新定义 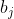 , 设
, 设 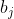 为长度为 j 的递增子序列的末尾最小值。这样的
为长度为 j 的递增子序列的末尾最小值。这样的 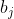 一定是有序的(为什么?这点很关键,这是时间上进行优化的基础)。 对于一个新的
一定是有序的(为什么?这点很关键,这是时间上进行优化的基础)。 对于一个新的  , 只需要将
, 只需要将  有序插入到
有序插入到 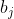 中即可。
中即可。
如果找得到插入的位置,那么就另  取代原该位置的元素(比如
取代原该位置的元素(比如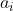 ,且一定有
,且一定有  )即可,表示
)即可,表示 的出现,使得
的出现,使得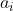 不再成为长度为
不再成为长度为 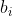 的递增子序列的最小末尾元素, 因为有更小的
的递增子序列的最小末尾元素, 因为有更小的  出现。
出现。
当找不到插入位置(即  大于任意一个
大于任意一个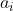 )时,表示
)时,表示  可以添加到任意一个已有递增子序列末尾构成长度加1的递增子序列,因此就将
可以添加到任意一个已有递增子序列末尾构成长度加1的递增子序列,因此就将  添加到数组
添加到数组 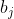 的末尾。最终数组
的末尾。最终数组 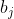 的长度即是原序列中最长递增子序列的长度。而
的长度即是原序列中最长递增子序列的长度。而
复杂度分析:由于数组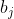 有序,所以插入操作可以使用二分查找法进行,复杂度是
有序,所以插入操作可以使用二分查找法进行,复杂度是 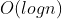 ,遍历原数组的时间是
,遍历原数组的时间是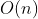 , 所以算法总的时间复杂度是
, 所以算法总的时间复杂度是 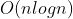 。
。
算法实现如下,题目是HDU 1025 :
//longest increment subsquence
#include <iostream>
#define MAXN 500001
using namespace std;
int a[MAXN];
void Insert(int* Min, int& nMin, int x)
{
int left = 0, right = nMin-1;
while(left<=right)
{
int mid = (left+right)/2;
if( Min[mid] < x )
{
left = mid+1;
}
else if( Min[mid] > x )
{
right = mid -1 ;
}
else return;
}
Min[left] = x;
if(left == nMin) nMin++;
}
int LIS(int n)
{
int* Min = new int[n];
int nMin = 1;
Min[0] = a[0];
for(int i = 1; i < n; i++)
{
Insert(Min, nMin, a[i]);
}
delete []Min;
return nMin;
}
int main()
{
int n;
int nCase = 1;
while(cin>>n)
{
int i;
for(i=1;i<=n;i++)
{
int j;
cin>>j;
cin>>a[j-1];
}
int lenth = LIS(n);
cout<<"Case "<<nCase++<<":"<<endl<<"My king, at most ";
if(lenth > 1) cout<<LIS(n)<<" roads can be built."<<endl<<endl;
else cout<<LIS(n)<<" road can be built."<<endl<<endl;
}
return 0;
}补充资料:
下面的分析截图来自于CSDN的论坛,不知道出自哪本书,仅供参考。




(四)最大递增子序列
最长递增子序列有一个变形的问题,如HDU 1087,题目意思是求一个序列中,各个元素之和最大的严格递增子序列。解决思路如LIS中的方法2,只不过令 b(j) 表示以 a[j] 结尾的递增子序列的最大值,最后再从数组b中找出数值最大的元素即可(也可以记录一个max变量,这样省略了一步遍历找最大值的过程)。
AC代码如下:
//hdu 1087
//dynamic programming
#include <iostream>
using namespace std;
int main()
{
int n;
while(cin>>n && n)
{
int* a = new int[n];
int* b = new int[n];
for(int i = 0 ; i < n; i++)
{
cin>>a[i];
b[i] = 0 ;
}
b[0] = a[0];
int max = a[0];
for(int i = 1; i < n; i++)
{
b[i] = a[i];
for(int j = 0 ; j < i ; j++)
{
if(a[i] > a[j] && b[j]+a[i]>b[i]) b[i] = b[j]+a[i];
}
if(max < b[i]) max=b[i];
/*
cout<<"level "<<i<<":";
for(int j = 0 ; j < n ;j++) cout<<b[j]<<" ";
cout<<endl;
*/
}
cout<<max<<endl;
}
return 0;
}算法的时间复杂度同LIS问题DP算法的方法2的时间复杂度。





















 3435
3435











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








