牛顿下降法和梯度下降法(最速下降法)的速度的比较

“牛顿下降法和梯度下降法在机器学习和自适应滤波中的都很重要，本质上是为了寻找极值点的位置。但是收敛的速度不同。 本文中就两种方法来探究一下，哪种收敛方法速度快“

---

牛顿下降法的递推公式：

$${x}_{n+1}={x}_{n}-f'({x}_{n})/f''({x}_{n})$$

梯度下降算法的递推公式：

$${x}_{n+1}={x}_{n}-\mu*f'({x}_{n})$$

<script type="math/tex; mode=display" id="MathJax-Element-3"></script>

解释一

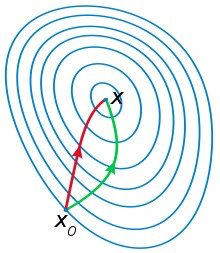
下图是两种方法的图示表示，红色为牛顿下降法，绿色为梯度下降法，从图中直观的感觉是，红色线短，下降速度快。因为牛顿下降法是用二次曲面去拟合当前的局部曲面，而梯度下降法是用平面去拟合当前的局部曲面，一般用二次曲面拟合的更好，所以一般牛顿算法收敛快。

关于以上的说法中，梯度下降法是用平面去拟合当前的局部曲面。梯度 f’(x)的方向是函数变大的方向。这里需要解释一下，对于一维情况而言，梯度方向只有正方向和负方向。至于为什么梯度下降算法就是用平面去拟合了，大多数情况下，没有讲的详细。接下来就聊一下为什么。

首先考虑一下这个公式，这是一阶泰勒展式，其实就是用平面去拟合函数的局部曲面。

f(x+