Trie树的常见应用大总结（面试+附代码实现）

（一）Trie的简介
Trie树，又称字典树，单词查找树或者前缀树，是一种用于快速检索的多叉树结构，如英文字母的字典树是一个26叉树，数字的字典树是一个10叉树。他的核心思想是空间换时间，空间消耗大但是插入和查询有着很优秀的时间复杂度。
（二）Trie的定义

Trie树的键不是直接保存在节点中，而是由节点在树中的位置决定。一个节点的所有子孙都有相同的前缀（prefix）,从根节点到当前结点的路径上的所有字母组成当前位置的字符串，结点可以保存当前字符串、出现次数、指针数组(指向子树)以及是否是结尾标志等等。

typedef struct Trie_Node
{
   	char count[15];      //单词前缀出现的次数 
   	struct Trie_Node* next[MAXN];    //指向各个子树的指针 
	bool exist;    //标记结点处是否构成单词 
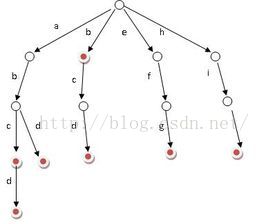
}Trie;

Trie树可以利用字符串的公共前缀来节约存储空间，如下图所示：

它有3个基本性质：
(1) 根节点不包含字符，除根节点外每一个节点都只包含一个字符。
(2) 从根节点到某一节点，路径上经过的字符连接起来，为该节点对应的字符串。
(3) 每个节点的所有子节点包含的字符都不相同。
（三）Trie树的基本操作
（1）插入操作
按下标索引逐个插入字母，若当前字母存在则继续下一个，否则new出当前字母的结点，所以插入的时间复杂度只和字符串的长度n有关，为O(n)。

void Insert(Trie *root, char* s,char *add)
{
	Trie *p=root;
	while(*s!='\0')
	{
		if(p->next[*s-'a']==NULL)
		{
			p->next[*s-'a']=createNode();
		}
		p=p->next[*s-'a'];
       // p->count=add;
        ++s; 
	}
	p->exist=true; 
    strcpy(p->count,add);
}

（2）查询操作
和插入操作相仿，若查询途中某一个结点并不存在，则直接就return返回。否则继续下去，当字符串结束时，trie树上也有结束标志，那么证明此字符串存在，return true；

int Search(Trie* root,const char* s)
{
	Trie *p=root;
	while(*s!='\0')
	{
		p=p->next[*s-'a'];
		if(p==NULL)
		return 0;
		++s;
	}
	return p->count;
}

（3）删除操作

一般来说，对Trie单个结点的删除操作不