熄灯问题 Lights Out Puzzle

From : http://mathworld.wolfram.com/LightsOutPuzzle.html

 

转化为高斯消元法，POJ 1222

 

---

 

Recreational Mathematics  >  Games  >  Board Games  >  Miscellaneous Board Games  >

Discrete Mathematics  >  Combinatorics  >  Designs  >

MathWorld Contributors  >  Barile  >

Interactive Entries  >  Interactive Demonstrations  >

 

Lights Out Puzzle

A one-person game played on a rectangular lattice of lamps which can be turned on and off. A move consists of flipping a "switch" inside one of the squares, thereby toggling the on/off state of this and all four vertically and horizontally adjacent squares. Starting from a randomly chosen light pattern, the aim is to turn all the lamps off. The problem of determining if it is possible to start from set of all lights being on to all lights being off is known as the "all-ones problem." As shown by Sutner (1989), this is always possible for a square lattice (Rangel-Mondragon).

This can be translated into the following algebraic problem.

1. Each lamp configuration can be viewed as a matrix with entries in (i.e., a binary matrix ), where each 1 represents a burning light and 0 represents a light turned off. For example, for the case,

(1)

2. The action of the switch placed at can be interpreted as the matrix addition , where is the matrix in which the only entries equal to 1 are those placed at and in the adjacent positions; there are essentially three different types of matrices , depending on whether is a corner entry,

(2)

a side entry,

(3)

or a middle entry,

(4)

3. Since matrix addition is commutative, it follows that the order in which the moves are performed is irrelevant.

4. Every winning combination of moves can be expressed mathematically in the form:

(5)

Here, denotes the zero matrix , which corresponds to the situation where all lights are turned off, and each coefficient represents the number of times that switch has to be pressed. Because we are solving the equations (mod 2), they can therefore be written in the equivalent form

(6)

Furthermore, it suffices to consider 0 and 1 as the only possible values for . Hence, the above equality is in fact a system of linear equations in the indeterminates over the field .

For example, the system corresponding to the initial (left) light pattern above can be written as

(7)

It has exactly one solution: ( , , ), which means that the game is solved by pressing the switches , , , and (corresponding to the red dots in the figure above). Since the matrix of the above system of equations has maximal rank (it is a matrix with nonzero determinant), the game on a -lattice is always solvable.

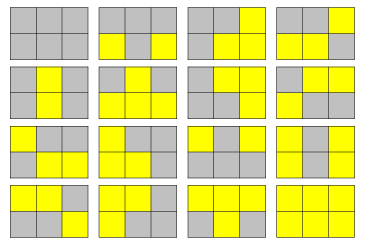
In general, the solvable patterns of the lattice are those which are obtained from the no-light pattern by pushing some switches. In the language of linear algebra, they are the -matrices which are sums of some matrices . For instance, the solvable patterns of the -lattice are illustrated above. All other rectangles of size or less are solvable for every possible starting pattern.

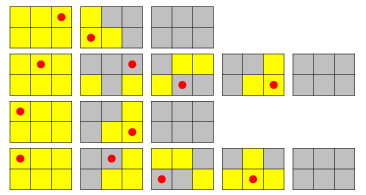
Multiple solutions are sometimes possible. For example, going from lights all on to all off in the case, there are four possible solutions to the all-lights pattern, illustrated above.

Some patterns have no solutions. For example, in the pattern shown above, it is impossible to turn off all the lights.

As shown by Sutner (1989), going from all lights on to all lights off is always possible for any size square lattice. The above illustration shows all possible solutions for to 7. The numbers of solutions (ignoring rotation and reflection) for , 2, ... are 1, 1, 1, 16, 4, 1, 1, 1, 256, 1, 64, 1, 1, 16, 1, ... (Sloane's A075462 ), and the corresponding minimal numbers of buttons to be pressed are 1, 4, 5, 4, 15, 28, 33, 40, 25, 44, 55, 72, 105, 56, 117, ... (Sloane's A075464 ). The board sizes with unique solutions (counting boards having equivalent solutions by rotation or reflections as distinct) are therefore 1, 2, 3, 6, 7, 8, 10, 12, 13, 15, 18, 20, ... (Sloane's A076436 ; Cowen and Kennedy 2000).

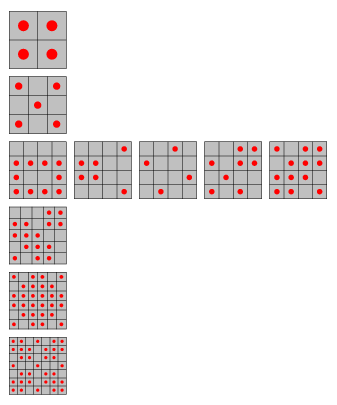
Removing solutions that are equivalent by rotation or reflection gives the distinct solutions illustrated above, of which there are 1, 1, 1, 5, 1, 1, 1, 1, 43, 1, 10, 1, 1, 5, 1, ... (Sloane's A075463 ). The board sizes with unique solutions (counting boards having equivalent solutions by rotation or reflections as equivalent) are therefore 1, 2, 3, 5, 6, 7, 8, 10, 12, 13, 15, 17, 18, ... (Sloane's A076437 ).

This entry contributed by Margherita Barile

REFERENCES:

Caro, Y. "Simple Proofs to Three Parity Theorems." Ars Combin. 42 , 175-180, 1996.

Conlon, M. M.; Falidas, M.; Forde, M. J.; Kennedy, J. W.; McIlwaine, S.; and Stern, J. "Inversion Numbers of Graphs." Graph Th. Notes New York 37 , 42-48, 1999.

Cowen, R. and Kennedy, J. "The Lights Out Puzzle." Math. Educ. Res. 9 , 28-32, 2000. http://library.wolfram.com/infocenter/Articles/1231/ .

Cowen, R.; Hechler, S. H.; Kennedy, J. W.; and Ryba, A. "Inversion and Neighborhood Inversion in Graphs." Graph Th. Notes New York 37 , 37-41, 1999.

Goldwasser, J. and Klostermeyer, W. "Maximization Versions of 'Lights Out' Games in Grids and Graphs." Congr. Numer. 126 , 99-111, 1997.

JavaScript Source. "Lights Out." http://javascript.internet.com/games/lights-out.html .

Millstone Website. "Lights Out." http://www.millstone.demon.co.uk/games/lightsout/start.htm .

Rangel-Mondragon, J. "A Catalog of Cellular Automata." http://library.wolfram.com/infocenter/MathSource/505/ .

Raguet-Schofield, R. "Lights Out Palette Demonstration." http://library.wolfram.com/infocenter/Demos/4817/ .

Sloane, N. J. A. Sequences A075462 , A075463 , A075464 , A076436 , and A076437 in "The On-Line Encyclopedia of Integer Sequences."

Sutner, K. "Linear Cellular Automata and the Garden-of-Eden." Math. Intelligencer 11 , 49-53, 1989.

Whitman College Department of Mathematics. "Lights Out." http://www.whitman.edu/offices_departments/mathematics/lights_out/ .

CITE THIS AS:

Barile, Margherita . "Lights Out Puzzle." From MathWorld --A Wolfram Web Resource, created by Eric W. Weisstein . http://mathworld.wolfram.com/LightsOutPuzzle.html