本讲主要列一下单峰搜索算法
问题:f(x)在区间[a,b]内只有一个极小值点,要找到这个极小值点或者这个极小值点所在的区间[x1,x2],其中[x1, x2]要远远小于[a, b]
方法:
一个通用的结论
要缩小区间,必须计算两个点,如果所示,必须计算x1和x2,然后对函数值进行比较。如果f(x1)小于f(x2),那么就说明极小值点一定在a到x2之间,反之也是这个思路。途中后面的两个式子将在以后的方法中反复使用。注意这了仅仅指的是单峰函数
具体的方法基本都是基于以上的思路,不同的是怎么确定x1和x2
具体的方法有
1. 二分搜索法(dichotomous search)
步骤一:首先找到[a,b]的中间点c,c=(a+b)/2,这就是“二分”的意思
步骤二:事先确定一个值sigma,在c左右各找二分之sigma,产生x1、x2。这个就是通用结论中的x1、x2
步骤三:按照通用结论中的方法来做
步骤四:循环确定区间[x1, x2],直到满足要求为止
查找速度:新区间的长度L(n+1),上一个区间的长度L(n),他们的关系是:L(n+1) = L(n)/2 + sigma/2
这个方法其实只是确定了x1和x2怎么找。
计算量:需要计算三个点
缺点:一是需要预先指定sigma,指定不好会有问题。二是得到x1、x2需要计算三个点
2. 等分区间搜索(equal-interval search)
三点等分(也就是区间四等分)
算法跟上面的基本一致,下面通过一个计算题描述一下<





 本文介绍了在单峰函数中寻找极小值点的一维搜索算法,包括二分搜索法和等分区间搜索法。二分搜索法通过不断将区间二分来逼近极小值点,而等分区间搜索法则将区间分为相等部分进行判断。两种方法都涉及到如何确定关键点x1和x2,并比较函数值以缩小搜索区间。
本文介绍了在单峰函数中寻找极小值点的一维搜索算法,包括二分搜索法和等分区间搜索法。二分搜索法通过不断将区间二分来逼近极小值点,而等分区间搜索法则将区间分为相等部分进行判断。两种方法都涉及到如何确定关键点x1和x2,并比较函数值以缩小搜索区间。
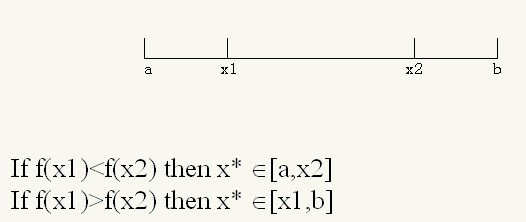
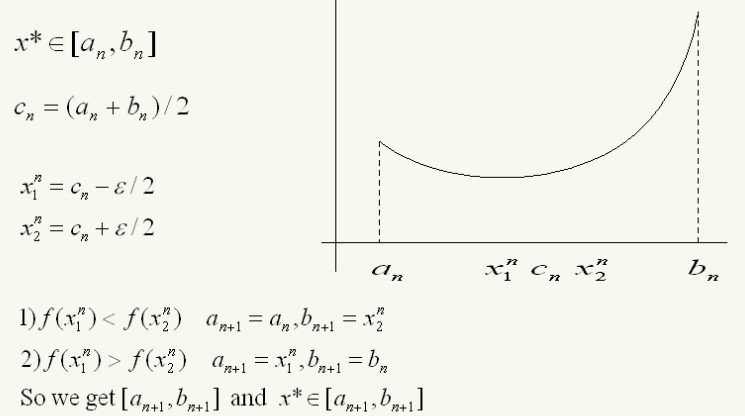
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 1753
1753

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








