快速排序

【0】README

0.1）正如它的名字所表示的，快速排序（quicksort）是在实践中最快的已知排序算法，它的平均运行时间是O(N log N)， 像归并排序一样，快速排序也是一种分治的递归算法；

---

【1】引入三数中值（中位数）分割法

1.1）方法描述：该方法的做法是使用左端、右端 和 中心位置上的三个元素组成序列的中值作为枢纽元；如输入8, 1, 4, 9, 6, 3, 5, 2, 7, 0 ；最左边元素是8，最右边元素是0，中心位置center = （left+right）/2 （向下取整）=(0+9)/2=4（向下取整）上的元素是6， 所以{8,0,6} 的中值是6，于是枢纽元是6；
Attention）三数中值分割法的源代码参见 https://github.com/pacosonTang/dataStructure-algorithmAnalysis/blob/master/chapter7/p182.c

1.2）补充说明-Complementary：

• C1）向上向下取整函数数只会对小数点后面的数字不为零的数进行操作，要是给它一个整数，它就返回整数本身；
• C2）向上取整：不管四舍五入的规则，只要后面有小数前面的整数就加1；
• C3）向下取整：不管四舍五入的规则，只要后面有小数忽略小数；
• C4）看个荔枝：给定 4.9 调用向下取整函数，得到的是 4； 调用向上取整函数得到的是 5 ；

---

【2】将数组S进行快速排序的步骤如下：

• step1）如果S中元素个数是0 或 1，则返回；
• step2）取S中任一元素 v，称为枢纽元（pivot） or 标兵；
• step3）将（S中其余元素）分成两个不相交的集合：S1 = { x ∈ S - { v } | x ≤ v } 和 S2 = { x ∈ S - { v } | x > v }；
• step4）对 集合 S1 和 S2 分别进行递归快速排序，转向step1；
• step5）最后将 S1 、S2 和 枢纽元 进行有序合并；

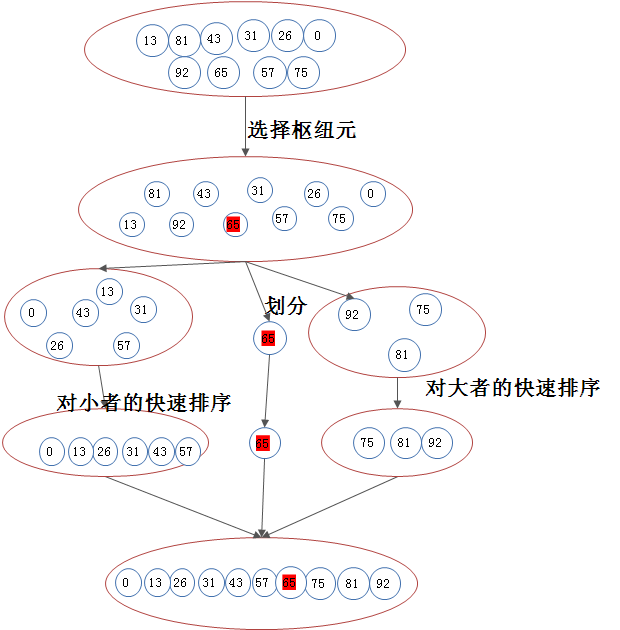
2.1）依据上述步骤对序列 13,81,92,43,65,31,57,26,75,0 进行第一趟划分处理，可得到如下图所示的过程：
Attention）：以下随机选 65 作为枢纽元；

2.2）接着，我们分析快速排序的5个步骤：

• step2） 选取枢纽元（使用第一个元素作为枢纽元是糟糕的主意，为什么？）
  我们采用的是 三数中值分割法， 见本文 章节 【1】；

• step3）分割策略

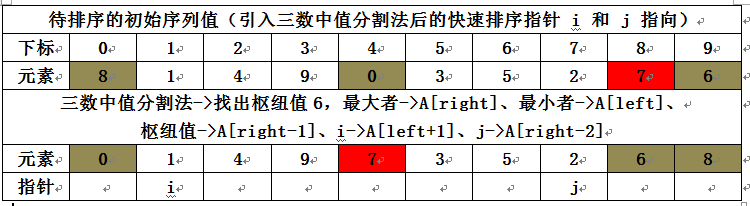
  • step3.1）初始状态： 通过将枢纽元与最后的元素交换使得枢纽元离开要被分割的数据段；i 从第一个元素开始而 j 从倒数第2个元素开始（这是快速排序习惯性规定的 i，j 初始指向）；状态如下：
    
    （要知道，分割的目的是让枢纽前面的元素小于枢纽元，其后元素大于枢纽元）

  • step3.2）实际的快速排序例程的 i 和 j 指向
    经过三数中值分割法后， 该三元素中的最小者被分在A[left]，最大者被分在A[right]， 他们都是正确（有序）的位置。故，我们把枢纽元放在A[right-1]，而 i 初始化指向 left + 1， j 初始化指向 right -2 （因为A[right]==最大者，A[right-1]=枢纽元，所以剩下的最右边的下标为right-2）；
    
    Alert）：三数中值分割法的代码中的 swap(&A[center], &A[right - 1]); 表明了 枢纽值 和 A[right-1] 进行交换；

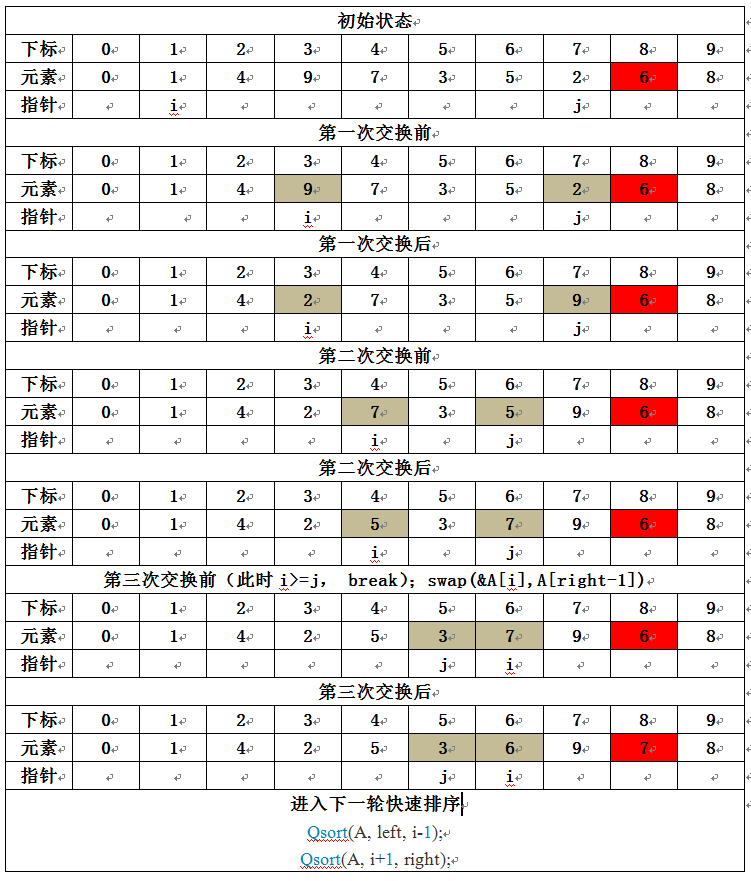
• step3.3）移动规则-Rule

  • R1）当 i 在 j 左边，将 i 右移，移过那些小于枢纽元的元素；
  • R2）将 j 左移， 移过那些大于枢纽元的元素；
  • R3）当 i 和 j 停止，i 指向大元素，j 指向小元素；
  • R4）若 i 在 j 的左边，将两元素交换，大元素移到右边，小元素移到左边；

• step3.4）移动状态-Status

  • S1）初始指针（i 和 j）状态 以及 经过三数中值分割法后的 待排序序列的元素分布，如下图：
    

• 补充-Complementary：如何处理那些等于枢纽元的关键字

  • C1）碰到等于枢纽元的关键字， i， j 都停止（停止意味着交换元素）。 如果i， j 不停止呢？会造成什么恶果？
  • C2）我们发现，进行不必要的交换建立两个均衡的子数组要比蛮干冒险得到两个不均衡的子数组要好， 而在碰到等于枢纽元的关键字时，i 和 j 都停止才能建立两个均衡的子数组 ；

• Attention）小数组
  意思是说对于小数组（N<=20）， 快速排序不如插入排序好。对于小数组，通常的解决方法是不使用快速排序，而是用插入排序。而一种好的截止范围是N=10； 特殊情况： 取三数中值时，数组却只有1个或2个元素；

• step4）实际的快速排序例程

  • step4.1）选取枢纽元的好处
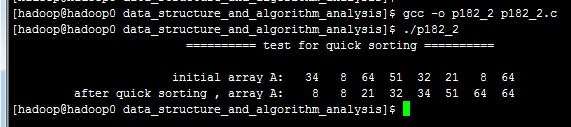
    该三元素中的最小者被分在A[left]，最大者被分在A[right]， 他们都是正确（有序）的位置。故，我们把枢纽元放在A[right-1]，而 i 初始化指向 left + 1， j 初始化指向 right -2 （因为A[right]==最大者，A[right-1]=枢纽元，所以剩下的最右边的下标为right-2）；
  • step4.2）结合step3 中的分割策略的移动规则，快速排序算法的源代码参见
    https://github.com/pacosonTang/dataStructure-algorithmAnalysis/blob/master/chapter7/p182_2.c ；打印结果如下：
    

• Attention）我们可以修改快速排序以解决选择问题，求 S 中第 k 个最小（大）元的算法几乎和快速排序相同，其前三步是一样的，我们把这种算法叫做快速选择（quick selection）