2017 ACM-ICPC 亚洲区（西安赛区）网络赛 F.Trig Function(论文+组合数)

传送门

$f(cos(x)) = cos(n*x)$ holds for all $x$.

Given two integers $n$ and $m$, you need to calculate the coefficient of $x^m$ in $f(x)$, modulo $998244353$.

Input Format

Multiple test cases (no more than $100$).

Each test case contains one line consisting of two integers $n$ and $m$.

$1 \le n \le 10^9,0 \le m \le 10 ^ 4$.

Output Format

Output the answer in a single line for each test case.

样例输入

2 0 

2 1 

2 2

样例输出

998244352 

0 

2

题目大意：

给出$f(cos(x)) = cos(n*x)$ ，求$x^m$前面的系数，其实就是求 $cos(x)^m$ 前面的系数。

解题思路：

首先给出论文：传送门
然后就根据论文进行计算就OK了，需要特判两个点。
给出组合数公式：

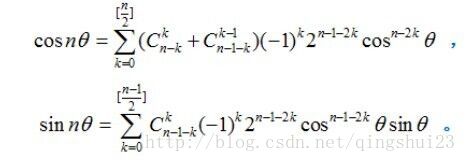
1) $m==0$ 的时候
2) $m==n$ 的时候

代码：

#include <iostream>
#include <string.h>
#include <string>
#include <algorithm>
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <map>
using namespace std;
typedef long long LL;
const int MAXN = 1e4+5;
const double PI = acos(-1);
const double eps = 1e-8;
const LL MOD = 998244353;
LL Pow(LL a, LL b){
    LL ans = 1;
    while(b){
        if(b & 1) ans = ans * a % MOD;
        b>>=1;
        a = a * a % MOD;
    }
    return ans;
}

LL Inv[MAXN];
void Init(){
    Inv[0] = Inv[1] = 1;
    for(int i=2; i<MAXN; i++) Inv[i] = (MOD - MOD / i) * Inv[MOD % i] % MOD;
    for(int i=2; i<MAXN; i++) Inv[i] = Inv[i]*Inv[i-1]%MOD;
}
int main(){
    //freopen("C:/Users/yaonie/Desktop/in.txt", "r", stdin);
    //freopen("C:/Users/yaonie/Desktop/out.txt", "w", stdout);
    Init();
    LL n, m;
    while(~scanf("%lld%lld", &n, &m)){
        if(((n&1)&&!(m&1)) || (!(n&1)&&(m&1))){
            puts("0");
            continue;
        }
        LL k = (n-m)/2;
        if(m == 0){
            if(k & 1) puts("998244352");
            else puts("1");
            continue;
        }
        if(n == m){
            printf("%lld\n",Pow(2LL, n-1));
            continue;
        }
        LL t1 = min(k, n-2*k), t2 = min(k-1, n-2*k);
        LL ans1 = Inv[t1], ans2 = Inv[t2];
        for(LL i=1; i<=t1; i++){
            LL tmp = (n-k-i+1)%MOD;
            ans1 = ans1*tmp%MOD;
        }
        for(LL i=1; i<=t2; i++){
            LL tmp = (n-k-i)%MOD;
            ans2 = ans2*tmp%MOD;
        }
        LL ans = (ans1 + ans2) % MOD;
        if(k & 1) ans=-ans;
        ans = (ans+MOD)%MOD;
        ans = ans*Pow(2LL, n-1-2*k)%MOD;
        printf("%lld\n",ans);
    }
    return 0;
}