监督学习中,如果预测的变量是离散的,我们称其为分类(如决策树,支持向量机等),如果预测的变量是连续的,我们称其为回归。回归分析中,如果只包括一个自变量和一个因变量,且二者的关系可用一条直线近似表示,这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量,且因变量和自变量之间是线性关系,则称为多元线性回归分析。对于二维空间线性是一条直线;对于三维空间线性是一个平面,对于多维空间线性是一个超平面...这里,谈一谈最简单的一元线性回归模型。
1.一元线性回归模型
模型如下:


总体回归函数中Y与X的关系可是线性的,也可是非线性的。对线性回归模型的“线性”有两种解释:
(1)就变量而言是线性的,Y的条件均值是 X的线性函数
(2)就参数而言是线性的,Y的条件均值是参数 的线性函数
的线性函数
线性回归模型主要指就参数而言是“线性”,因为只要对参数而言是线性的,都可以用类似的方法估计其参数。
2.参数估计——最小二乘法
对于一元线性回归模型, 假设从总体中获取了n组观察值(X1,Y1),(X2,Y2), …,(Xn,Yn)。对于平面中的这n个点,可以使用无数条曲线来拟合。要求样本回归函数尽可能好地拟合这组值。综合起来看,这条直线处于样本数据的中心位置最合理。 选择最佳拟合曲线的标准可以确定为:使总的拟合误差(即总残差)达到最小。有以下三个标准可以选择:
(1)用“残差和最小”确定直线位置是一个途径。但很快发现计算“残差和”存在相互抵消的问题。
(2)用“残差绝对值和最小”确定直线位置也是一个途径。但绝对值的计算比较麻烦。
(3)最小二乘法的原则是以“残差平方和最小”确定直线位置。用最小二乘法除了计算比较方便外,得到的估计量还具有优良特性。这种方法对异常值非常敏感。
最常用的是普通最小二乘法( Ordinary Least Square,OLS):所选择的回归模型应该使所有观察值的残差平方和达到最小。(Q为残差平方和)
样本回归模型:
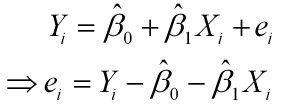
残差平方和:
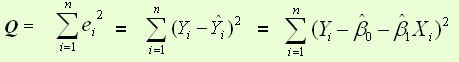
则通过Q最小确定这条直线,即确定 ,以
,以 为变量,把它们看作是Q的函数,就变成了一个求极值的问题,可以通过求导数得到。求Q对两个待估参数的偏导数:
为变量,把它们看作是Q的函数,就变成了一个求极值的问题,可以通过求导数得到。求Q对两个待估参数的偏导数:
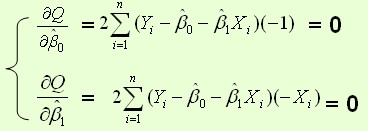
解得:
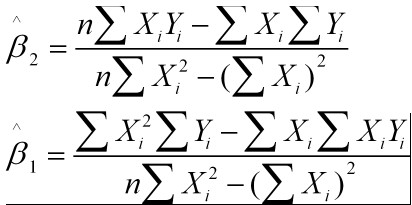
3.最小二乘法c++实现
#include<iostream>
#include<fstream>
#include<vector>
using namespace std;
class LeastSquare{
double a, b;
public:
LeastSquare(const vector<double>& x, const vector<double>& y)
{
double t1=0, t2=0, t3=0, t4=0;
for(int i=0; i<x.size(); ++i)
{
t1 += x[i]*x[i];
t2 += x[i];
t3 += x[i]*y[i];
t4 += y[i];
}
a = (t3*x.size() - t2*t4) / (t1*x.size() - t2*t2);
//b = (t4 - a*t2) / x.size();
b = (t1*t4 - t2*t3) / (t1*x.size() - t2*t2);
}
double getY(const double x) const
{
return a*x + b;
}
void print() const
{
cout<<"y = "<<a<<"x + "<<b<<"\n";
}
};
int main(int argc, char *argv[])
{
if(argc != 2)
{
cout<<"Usage: DataFile.txt"<<endl;
return -1;
}
else
{
vector<double> x;
ifstream in(argv[1]);
for(double d; in>>d; )
x.push_back(d);
int sz = x.size();
vector<double> y(x.begin()+sz/2, x.end());
x.resize(sz/2);
LeastSquare ls(x, y);
ls.print();
cout<<"Input x:\n";
double x0;
while(cin>>x0)
{
cout<<"y = "<<ls.getY(x0)<<endl;
cout<<"Input x:\n";
}
}
}





 本文介绍了监督学习中的一种基本回归方法——一元线性回归。重点讲解了一元线性回归模型的概念及其参数估计方法,并提供了最小二乘法的具体实现过程。
本文介绍了监督学习中的一种基本回归方法——一元线性回归。重点讲解了一元线性回归模型的概念及其参数估计方法,并提供了最小二乘法的具体实现过程。
















 6043
6043










