此文章可以使用目录功能哟↑(点击上方[+])
比赛链接→Codeforces Round #369 (Div. 2)
 Codeforces Problem 711C Coloring Trees
Codeforces Problem 711C Coloring Trees
Accept: 0 Submit: 0
Time Limit: 2 seconds Memory Limit : 256 megabytes
 Problem Description
Problem Description
ZS the Coder and Chris the Baboon has arrived at Udayland! They walked in the park where n trees grow. They decided to be naughty and color the trees in the park. The trees are numbered with integers from 1 to n from left to right.
Initially, tree i has color ci. ZS the Coder and Chris the Baboon recognizes only m different colors, so 0 ≤ ci ≤ m, where ci = 0 means that tree i is uncolored.
ZS the Coder and Chris the Baboon decides to color only the uncolored trees, i.e. the trees with ci = 0. They can color each of them them in any of the m colors from 1 to m. Coloring the i-th tree with color j requires exactly pi, j litres of paint.
The two friends define the beauty of a coloring of the trees as the minimum number of contiguous groups (each group contains some subsegment of trees) you can split all the n trees into so that each group contains trees of the same color. For example, if the colors of the trees from left to right are 2, 1, 1, 1, 3, 2, 2, 3, 1, 3, the beauty of the coloring is 7, since we can partition the trees into 7 contiguous groups of the same color : {2}, {1, 1, 1}, {3}, {2, 2}, {3}, {1}, {3}.
ZS the Coder and Chris the Baboon wants to color all uncolored trees so that the beauty of the coloring is exactly k. They need your help to determine the minimum amount of paint (in litres) needed to finish the job.
Please note that the friends can't color the trees that are already colored.
 Input
Input
The first line contains three integers, n, m and k (1 ≤ k ≤ n ≤ 100, 1 ≤ m ≤ 100) — the number of trees, number of colors and beauty of the resulting coloring respectively.
The second line contains n integers c1, c2, ..., cn (0 ≤ ci ≤ m), the initial colors of the trees. ci equals to 0 if the tree number i is uncolored, otherwise the i-th tree has color ci.
Then n lines follow. Each of them contains m integers. The j-th number on the i-th of them line denotes pi, j (1 ≤ pi, j ≤ 10^9) — the amount of litres the friends need to color i-th tree with color j. pi, j's are specified even for the initially colored trees, but such trees still can't be colored.
 Output
Output
Print a single integer, the minimum amount of paint needed to color the trees. If there are no valid tree colorings of beauty k, print - 1.
 Sample Input
Sample Input
0 0 0
1 2
3 4
5 6
3 2 2
2 1 2
1 3
2 4
3 5
3 2 2
2 0 0
1 3
2 4
3 5
3 2 3
2 1 2
1 3
2 4
3 5
 Sample Output
Sample Output
-1
5
0
 Hint
Hint
In the first sample case, coloring the trees with colors 2, 1, 1 minimizes the amount of paint used, which equals to 2 + 3 + 5 = 10. Note that 1, 1, 1 would not be valid because the beauty of such coloring equals to 1 ({1, 1, 1} is a way to group the trees into a single group of the same color).
In the second sample case, all the trees are colored, but the beauty of the coloring is 3, so there is no valid coloring, and the answer is - 1.
In the last sample case, all the trees are colored and the beauty of the coloring matches k, so no paint is used and the answer is 0.
 Problem Idea
Problem Idea
解题思路:
【题意】
公园有n棵树,有些已经被涂上颜色,有些还未上色
现在有m种不同颜色的颜料,给还未上色的树涂上颜色
已知对于第i棵树,若用颜料j来上色,需要的使用量为P(i,j)升
问美丽度恰好为k时,最少需要多少升颜料
美丽度的定义为连续颜色段的段数
如2, 1, 1, 1, 3, 2, 2, 3, 1, 3,它的美丽度为7,因为它有7个连续颜色段,分别为{2},{1,1,1},{3},{2,2},{3},{1},{3}
【类型】
动态规划(DP)
【分析】
显然,这是一道DP题,状态转移方程也是比较好想到的,只是敢不敢去写罢了(毕竟想想复杂度还是有点可怕)
令dp[i][j][l]表示第i颗树涂颜色l,美丽度为j时前i棵树共用颜料的升数
即,当第i棵树是本身已经上了色的,那我们就没有必要再上色了,前i棵树总共用的颜料当然就跟前i-1棵树总共用的颜料一样多
但前i-1棵树总共用的颜料又和第i-1棵树是什么颜色有关,若第i-1棵树的颜色与第i棵树颜色相同,那么美丽度没有增加;否则,第i-1棵树与第i棵树颜色不相同,美丽度就增加了1
若第i棵树未上色,那我就需要分析第i棵树涂颜色1~颜色m每种情况所需要的颜料量,方便对第i+1棵树进行分析
剩下的就是一些小细节的处理,注意一点就可以了,具体的见代码,有问题欢迎提出来
【时间复杂度&&优化】
O(nkm^2)
题目链接→Codeforces Problem 711C Coloring Trees
 Source Code
Source Code
/*Sherlock and Watson and Adler*/
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<queue>
#include<stack>
#include<math.h>
#include<vector>
#include<map>
#include<set>
#include<bitset>
#include<cmath>
#include<complex>
#include<string>
#include<algorithm>
#include<iostream>
#define eps 1e-9
#define LL long long
#define PI acos(-1.0)
#define bitnum(a) __builtin_popcount(a)
using namespace std;
const int N = 105;
const int M = 100005;
const __int64 inf = 1e18;
const int mod = 1000000007;
__int64 dp[N][N][N];
int c[N],p[N][N];
int main()
{
int n,m,k,i,j,l,q;
__int64 Min=inf;
scanf("%d%d%d",&n,&m,&k);
for(i=1;i<=n;i++)
scanf("%d",&c[i]);
for(i=1;i<=n;i++)
for(j=1;j<=m;j++)
scanf("%d",&p[i][j]);
for(i=0;i<=n;i++)
for(j=0;j<=k;j++)
for(l=0;l<=m;l++)
dp[i][j][l]=inf;
if(c[1])
dp[1][1][c[1]]=0;
else
for(i=1;i<=m;i++)
dp[1][1][i]=p[1][i];
for(i=2;i<=n;i++)
for(j=1;j<=k;j++)
if(c[i])
{
dp[i][j][c[i]]=min(dp[i][j][c[i]],dp[i-1][j][c[i]]);
for(l=1;l<=m;l++)
if(l!=c[i])
dp[i][j][c[i]]=min(dp[i][j][c[i]],dp[i-1][j-1][l]);
}
else
{
for(l=1;l<=m;l++)
{
dp[i][j][l]=min(dp[i][j][l],dp[i-1][j][l]+p[i][l]);
for(q=1;q<=m;q++)
if(q!=l)
dp[i][j][l]=min(dp[i][j][l],dp[i-1][j-1][q]+p[i][l]);
}
}
for(i=1;i<=m;i++)
Min=min(Min,dp[n][k][i]);
if(Min!=inf)
printf("%I64d\n",Min);
else
puts("-1");
return 0;
}










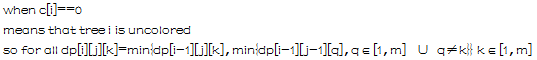














 837
837

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








