Splay总结

最新推荐文章于 2021-09-06 14:49:50 发布

slongle_amazing

最新推荐文章于 2021-09-06 14:49:50 发布

阅读量3.3k

点赞数 2

分类专栏：数据结构—Splay 模板/总结

本文链接：https://blog.csdn.net/slongle_amazing/article/details/49932813

版权

模板/总结同时被 2 个专栏收录

13 篇文章 0 订阅

订阅专栏

数据结构—Splay

11 篇文章 0 订阅

订阅专栏

论文汇总

链接: http://pan.baidu.com/s/1i3waHBR 密码: cfy5
个人感觉讲的比较清楚的(百度云里都包括,贴一下百度文库方便查看)
The Magical Splay
BST 拓展与伸展树 (Splay) 一日通
 杨思雨 2004国家集训队论文《伸展树的基本操作与应用》

浅谈平衡树

平衡树种类

平衡树通过旋转操作来使自身达到平衡状态,这其中例如Treap,Splay是均摊 $O(logN)$ ,而例如SBT是严格平衡严格 $O(logN)$

平衡树性质

对于一个节点i,它的leftson[i] (包括一个点或整个子树)的权值都小于节点i,它的rightson[i] (包括一个点或整个子树)的权值都大于节点i
平衡树是依靠整棵树的中序遍历来维护整个序列的

Splay的旋转和伸展操作

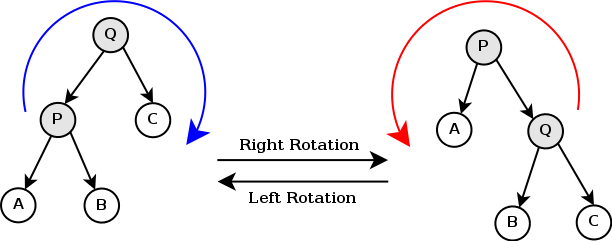
旋转

Splay分为左旋(zag),右旋(zig),通过组合我们又可以得到zig-zig,zag-zag,zig-zag,其中可以证明zig-zag=zig+zag,所以我们只需要zig,zag,zig-zig,zag-zag,考虑对称性,就分为单旋和双旋了

单旋

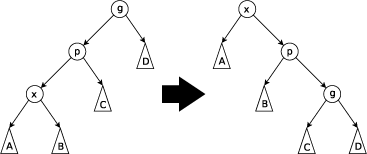
这里写图片描述

双旋

这里写图片描述

对于双旋我们也是可以把它摘成两步单旋的
比如上图,我们先对p右旋,再对x右旋即可
综上就只有左右单旋就可实现所有旋转操作了
从code角度来讲,左右旋是可以写成一个的
w[a,i],i=1:左儿子2:右儿子3:父4:子树节点和5:该权值个数6:权值
特意说一下w[a,5]:该权值个数,他存在的原因是因为插入时可能是重复的,而旋转操作的其中一个原因是二叉树的严格左儿子<该节点<右儿子,所以插入时重复的直接在w[a,5]上+1即可

procedure rotate(a,kind:longint); //kind=1右旋；kind=2左旋
var b,unkind;
begin
    b:=w[a,3]; unkind:=kind xor 3;
    w[a,4]:=w[b,4]; dec(w[b,4],w[a,5]+w[w[a,kind],4]);
    w[w[a,unkind],3]:=b; w[b,kind]:=w[a,unkind];
    w[a,unkind]:=b; w[a,3]:=w[b,3]; w[b,3]:=a;
    if w[a,3]<>-1
    then 
        if w[w[a,3],1]=b
        then w[w[a,3],1]:=a
        else w[w[a,3],2]:=a;
end;

伸展

Splay的均摊复杂度为每次O(logN)就是靠着每次将要操作的节点提为根节点来维持的
以下我们以a为操作节点,b=fa[a]来说
$我们定义a为它父节点的左儿子(son[b,1]=a)那么kind=1反之kind=2$
$它父节点的另一个儿子为unkind(unkind=kind~xor~3)$

zig/zag

$a的父节点为目标节点时执行此操作$

zig-zig/zag-zag

$a,a的父节点,a的父节点的父节点为同一侧的子节点$

zig-zag

$a,a的父节点,a的父节点的父节点为不同侧的子节点$

procedure splay(a,goal:longint);
var b,kind,unkind:longint;
begin
    while w[a,3]<>goal do
        begin
            b:=w[a,3]; if w[b,1]=a then kind:=1 else kind:=2; unkind:=kind xor 3;
            if w[b,3]=goal then rotate(a,kind)
            else 
                if w[w[b,3],kind]=b 
                then begin rotate(b,kind); rotate(a,kind); end
                else begin rotate(a,kind); rotate(a,unkind); end;
        end;
    if goal=-1 then root:=a;
end;

Splay支持的操作

root表示splay的根,sum表示最后一个节点在数组的位置

插入{init(a)}

注意有重复的问题

procedure init(a:longint);
var tt,fa,kind:longint;
begin
    tt:=root;
    while tt<>-1 do
        begin
            //标记下传 if w[tt,7]<>0 then pushdown(tt);
            inc(w[tt,4]); fa:=tt;
            if w[tt,6]=a then break;
            if a<w[tt,6]
            then begin tt:=w[tt,1]; kind:=1; end
            else begin tt:=w[tt,2]; kind:=2; end;
        end;
    if tt<>-1 
    then begin inc(w[tt,5]); splay(tt,-1); end
    else begin inc(sum); w[sum,1]:=-1; w[sum,2]:=-1; w[sum,3]:=fa; w[sum,4]:=1; w[sum,5]:=1; w[sum,6]:=a; w[fa,kind]:=sum; splay(sum,-1); end;
end;

删除{del(a)}

还是注意重复问题

function getmax(a:longint):longint; //在a的子树中找到最大的节点
var tt:longint;
begin
    tt:=a;
    while w[tt,2]<>-1 do
        tt:=w[tt,2];
    exit(tt);
end;

procedure del(a:longint);
var tt:longint;
begin
    tt:=root;
    while w[tt,6]<>a do
        if a<w[tt,6]
        then tt:=w[tt,1]
        else tt:=w[tt,2];
    splay(tt,-1);
    if w[tt,5]>1
    then begin dec(w[tt,4]); dec(w[tt,5]); end
    else begin splay(getmax(w[root,1]),root); w[w[root,1],2]:=w[root,2]; w[w[root,1],4]:=w[root,4]-1; root:=w[root,1]; w[w[root,2],3]:=root; w[root,3]:=-1; end;
end;

Splay和线段树

我们可以很容易地将任何一条线段用Splay夹出来,由于Splay也是一棵二叉树与线段树相似,所以就产生了Splay的特殊操作:翻转操作(就是打标记下传,没什么区别)

关于复杂度

时间复杂度为每次操作均摊 $O(logN)$ ,但常数问题…,~~势能分析得到的常数大概是...~~

Splay模板

const
    maxn=100005;
var
    w:array[-1..maxn,1..6]of longint;
    i,j,k:longint;
    n,sum,root,a,b:longint;
procedure print(a:longint);
var i:longint;
begin
    if w[a,1]<>-1 then print(w[a,1]);
    for i:=1 to w[a,5] do write(w[a,6],' ');
    if w[a,2]<>-1 then print(w[a,2]);
    if a=root then writeln;
end;

procedure rotate(a,kind:longint);
var b,unkind:longint;
begin
    b:=w[a,3]; unkind:=kind xor 3;
    w[a,4]:=w[b,4]; dec(w[b,4],w[a,5]+w[w[a,kind],4]);
    w[b,kind]:=w[a,unkind];
    w[w[a,unkind],3]:=b;
    w[a,unkind]:=b;
    w[a,3]:=w[b,3];
    w[b,3]:=a;
    if w[a,3]<>-1
    then
        if w[w[a,3],1]=b
        then w[w[a,3],1]:=a
        else w[w[a,3],2]:=a;
end;

procedure splay(a,goal:longint);
var b,kind,unkind:longint;
begin
    while w[a,3]<>goal do
        begin
            b:=w[a,3];
            if w[b,1]=a then kind:=1 else kind:=2; unkind:=kind xor 3;
            if w[b,3]=goal then rotate(a,kind)
            else
                if w[w[b,3],kind]=b
                then begin rotate(b,kind); rotate(a,kind); end
                else begin rotate(a,kind); rotate(a,unkind); end;
        end;
    if goal=-1 then root:=a;
end;

procedure init(a:longint);
var tt,fa,kind:longint;
begin
    tt:=root;
    while tt<>-1 do
        begin
            inc(w[tt,4]);
            if w[tt,6]=a then break;
            fa:=tt;
            if a<w[tt,6]
            then begin kind:=1; tt:=w[tt,1]; end
            else begin kind:=2; tt:=w[tt,2]; end;
        end;
    if w[tt,6]=a
    then inc(w[tt,5])
    else begin inc(sum); w[sum,1]:=-1; w[sum,2]:=-1; w[sum,3]:=fa; w[sum,4]:=1; w[sum,5]:=1; w[sum,6]:=a; w[fa,kind]:=sum; tt:=sum; end;
    splay(tt,-1);
end;

function getmax(a:longint):longint;
var tt:longint;
begin
    tt:=a;
    while w[tt,2]<>-1 do
        tt:=w[tt,2];
    exit(tt);
end;

function getmin(a:longint):longint;
var tt:longint;
begin
    tt:=a;
    while w[tt,1]<>-1 do
        tt:=w[tt,1];
    exit(tt);
end;

procedure del(a:longint);
var tt:longint;
begin
    tt:=root;
    while w[tt,6]<>a do
        if a<w[tt,6]
        then tt:=w[tt,1]
        else tt:=w[tt,2];
    splay(tt,-1);
    if w[root,5]=1
    then 
        begin
            splay(getmax(w[root,1]),root);
            w[w[root,1],2]:=w[root,2]; w[w[root,1],4]:=w[root,4]-1; root:=w[root,1]; w[w[root,2],3]:=root; w[root,3]:=-1;
        end
    else 
        begin dec(w[root,5]); dec(w[root,4]); end;
end;

function getrank(a:longint):longint;
var tt:longint;
begin
    tt:=root;
    while w[tt,6]<>a do
        if a<w[tt,6]
        then tt:=w[tt,1]
        else tt:=w[tt,2];
    splay(tt,-1);
    exit(w[w[tt,1],4]);
end;

function getkth(a:longint):longint;
var tt:longint;
begin
    tt:=root;
    while (a<=w[w[tt,1],4])or(a>w[w[tt,1],4]+w[tt,5]) do
        if a<=w[w[tt,1],4]
        then tt:=w[tt,1]
        else begin dec(a,w[w[tt,1],4]+w[tt,5]); tt:=w[tt,2]; end;   
    exit(w[tt,6]);
end;

begin
    readln(n); sum:=2; root:=2;
    w[1,1]:=-1; w[1,2]:=-1; w[1,3]:=2; w[1,4]:=1; w[1,5]:=1; w[1,6]:=-1000000005;
    w[2,1]:=1; w[2,2]:=-1; w[2,3]:=-1; w[2,4]:=2; w[2,5]:=1; w[2,6]:=1000000005;
    for i:=1 to n do
        begin
            readln(a,b);
            case a of
            1:begin init(b); end;
            2:begin del(b); end;
            3:begin writeln(getrank(b)); end;
            4:begin writeln(getkth(b+1)); end;
            5:begin init(b); writeln(w[getmax(w[root,1]),6]); del(b); end;
            6:begin init(b); writeln(w[getmin(w[root,2]),6]); del(b); end;
            end;
    end;
end.

Splay模板题

[BZOJ3223] Tyvj 1729 文艺平衡树关于翻转标记
[BZOJ3224] Tyvj 1728 普通平衡树平衡树基本操作
[BZOJ1503] [NOI2004]郁闷的出纳员带+-标记的平衡树
[BZOJ1208] [HNOI2004]宠物收养所
 [BZOJ1251] 序列终结者注意标记下放的过程

slongle_amazing

关注

2
点赞
踩
3

收藏

觉得还不错? 一键收藏
0
评论
Splay总结

论文汇总链接: http://pan.baidu.com/s/1i3waHBR 密码: cfy5 个人感觉讲的比较清楚的(百度云里都包括,贴一下百度文库方便查看) The Magical Splay BST 拓展与伸展树 (Splay) 一日通杨思雨 2004国家集训队论文《伸展树的基本操作与应用》浅谈平衡树平衡树种类平衡树通过旋转操作来使自身达到平衡状态,这其中例如Treap,Spl
复制链接

扫一扫