最短路径算法--无权最短路径

简介

  输入是一个赋权图：与每条边（v_i，v_j）相联系的是穿越该弧的代价（或称为值）c_i,j。一条路径v₁v₂v₃…v_N的值是，叫做赋权路径长（weighted path length），而无权路径长（unweighted path length）只是路径上的边数，即N-1。

单源路径问题

  给定一个赋权图G=（V，E）和一个特定顶点s作为输入，找出从s到G中每一个其它顶点的最短赋权路径。

  负值圈（negative-cost cycle）：带圈图中圈中的权值有为负值。当它出现在图中时，最短路径问题就是不确定的。

无权最短路径

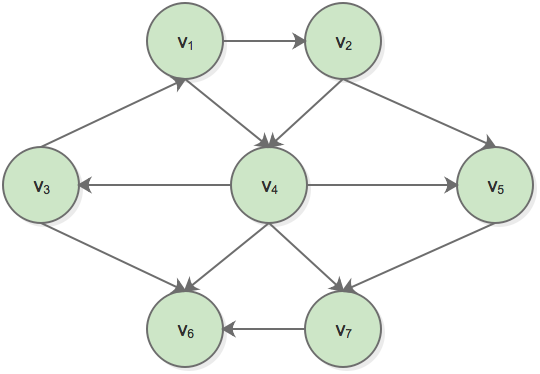
下图是一个无权图G，使用某个顶点s作为输入参数，我们想要找出从s到所有其它顶点的最短路径。我们只对包含在路径中的边数有兴趣，因此在边上不存在权。显然，这是赋权最短路径问题的特殊情形，因为我们可以为所有的边都赋以权1。一个无权有向图G：

<