所谓串的模式匹配,简单说就是指给定一个主串T(text)和一个子串P(pattern),求在T中第一次出现P的位置索引。例如T=”timercrack likes to sleep”,P=”likes”,则P在T中的位置索引为12。
首先,让我们来看一种朴素的匹配算法,设T[n]存放主串,P[m]存放子串(模式串),则算法可以这样描述:
 //
朴素的模式匹配算法
//
朴素的模式匹配算法

 int
Index(
string
T,
string
P,
int
pos)
{
int
Index(
string
T,
string
P,
int
pos)
{ //返回模式串P在主串T第pos个字符之后的位置。
//返回模式串P在主串T第pos个字符之后的位置。 //其中1<=pos<=T.length
//其中1<=pos<=T.length i = pos; j = 1;
i = pos; j = 1; while (i <= T.length && j <= P.length)
while (i <= T.length && j <= P.length)
 if (T[i] == P[j]) {
if (T[i] == P[j]) { ++i;
++i; ++j;
++j;
 } else {
} else { i = i–j + 2;
i = i–j + 2; j = 1;
j = 1;  }
} //匹配成功返回位序,否则返回-1
//匹配成功返回位序,否则返回-1 retun j > T.length ? i–T.length : -1;
retun j > T.length ? i–T.length : -1; }
//
Index
}
//
Index
每一轮匹配j最多加到m,最多匹配n轮,所以算法的时间复杂度是O(m*n)。匹配的过程十分清晰,这里关键要注意当某次失配时(即T[i]≠P[j]),i会退回到本次匹配开始的下一个字符处,重新和T[1]开始比较。这导致在某些情况下算法的效率非常低,例如:P=”00000001”,T=”000000000...0001”,每次匹配到P[8]与T[i]不相等时,i要回退j-2=6个字符,并重新和P[1]进行比较。
因此我们想,在每次失配时能不能不让i回退,而只让模式串向右“滑动一段距离”呢?举个例子:
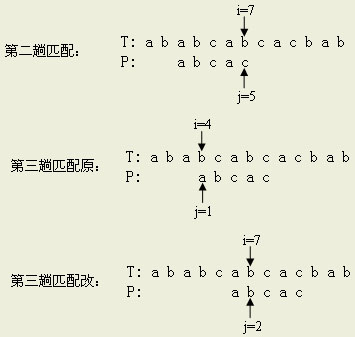
如上图,在第二趟匹配失配时i回到了4位置,与P[1]重新比较。而实际上T[4]与P[1]、T[5]与P[1]、T[6]与P[1]这三次比较是多余的,因为在第二趟匹配时我们已经知道它们是“bca”。因为模式串的首字符是a,刚好与T[6]相同,所以可保持i不变,让j=2再与T[i]比较。形象说就是让模式串相对于主串“向右滑动”3个字符。正如上图中最后的“第三趟匹配改”所做的那样。
本着这个思想我们来讨论一下如何改进这个算法。通过前面的简单介绍我们知道,在某些情况下当某一次匹配失败时,可以将模式串向右滑动一段距离。那么,为什么可以这样呢?换句话说,每次可以滑动多远呢?下面我们来分析一下:设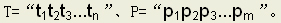 若某一次T[i]≠P[j]时,假设可以保持i
若某一次T[i]≠P[j]时,假设可以保持i
不变,让P向右滑动一段距离,设此时j=k,程序将继续比较T[i]与P[j]是否相等。那么必然有如下等式(1):
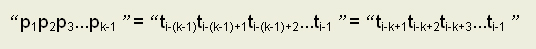
式(1)说明位置k之前的k-1个字符已经与主串i之前的k-1个字符相等,而目前已有P串的前j-1个字符与主串匹配成功,因为k<j,显然有:
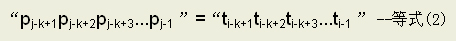
由(1)(2)式可得出:
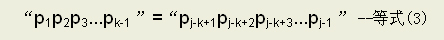
等式(3)就是P可以滑动的依据,当P向右滑动至j=k时,P之前的k-1个字符必与主串T从i向前数k-1个字符相等。也就是说能滑动的前提是模式串中存在两个相等的子串,并且一:其中一个子串必须从P首开始;二:两个子串在P中可以部分重叠。如下所示:
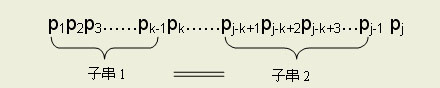
为了便于实现,我们定义一维数组next[],并规定next[j](1≤j≤m)表示当T[i]≠P[j]时,在模式串中须重新与T[i]相比较的位置(next[j]=k)。例如对于模式串P=“abaabcac”,其next数组的值为:

我们规定next[1]=0,用来表示数组的起始值,这个规定是随意的,如果乐意完全可以改成别的值(设成0是为了算法的简洁,这在后面将会看到)。
好了,我们先假设有某种方法计算next[]数组的值,那么匹配可以这样进行:当T[i]≠P[j]时,令j=next[j]再继续与T[i]进行比较。若仍不相等再令j=next[j],重复上述过程,直到退至某一next[k]时T[i]=P[next[k]];或退到j=next[1]=0,说明模式串的首字符与T[i]失配,则将i++,继续下一轮的匹配。下面给出这种改进的匹配算法:
 //
改进的模式匹配算法
//
改进的模式匹配算法

 int
Index(
string
T,
string
P,
int
pos)
{
int
Index(
string
T,
string
P,
int
pos)
{ //利用数组next[]求模式串P在主串T第pos个字符之后的位置。
//利用数组next[]求模式串P在主串T第pos个字符之后的位置。 //其中1<=pos<=T.length
//其中1<=pos<=T.length i = pos; j = 1;
i = pos; j = 1; while (i <= T.length && j <= P.length)
while (i <= T.length && j <= P.length)
 if (j == 0 || T[i] == P[j]) {
if (j == 0 || T[i] == P[j]) { ++i;
++i; ++j;
++j; } else j = next[j]; //模式串向右滑动
} else j = next[j]; //模式串向右滑动 //匹配成功返回位序,否则返回-1
//匹配成功返回位序,否则返回-1 retun j > T.length ? i – T.length : -1;
retun j > T.length ? i – T.length : -1; }
//
Index
}
//
Index
该算法最初是在1968年由D.E.Knuth和他的学生J.H.Morris和V.R.Pratt首先发现的,简称为KMP算法,取了这三个人名字的首字母。这时,或许你突然明白了AVL 树为什么叫AVL,或者Bellman-Ford为什么中间是一杠不是一个点。有时一个东西有七八个人研究过,那怎么命名呢?通常这个东西干脆就不用人名字命名了,免得发生争议,比如“3x+1问题”......扯远了。
书上只是简单说这个程序的时间复杂度是O(n),并没有解释,但为什么是O(n)呢?其实主要的争议在于,每次是执行if语句体还是执行else语句使得while循环的执行次数出现了不确定因素。我们将用时间复杂度的摊还分析中的主要策略来分析它,简单地说就是通过观察某一个变量或函数值的变化来对零散的、杂乱的、不规则的执行次数进行累计。KMP的时间复杂度分析可谓摊还分析的典型。我们从上述程序的j 值入手。每一次执行第六句if语句体都会使j加1(但不能大于m),而另外的改变j值的地方只有第六行一处(else j=next[j])。每一次执行这句j都会减少;因此,整个过程中j最多加了m-1个1。于是,j最多只有m-1次减小的机会(j值减小的次数当然不能超过m,因为j永远是非负整数)。这告诉我们,else语句最多执行了m-1次。按照摊还分析的说法,平摊到每次while循环中后,一次while循环的时间复杂度为O(1)。整个过程显然是O(n)的。
上面的都清楚以后,现在让我们来讨论next数组值的求法。由等式(3)可知,next的值只与模式串P本身有关,与主串没有关系。由next的定义可知当j>1时next[j]等于集合{k | 1<k<j且k满足等式(3)}中的最大值,当集合为空时next[j]=1。所以可以使用一种“递推”的方法来求next,这种方法类似于我们使用数学归纳法证明定理,所不同的是在证明定理时我们已经知道定理的结果,而现在结果并不知道,需要我们一步步推出它。
已知next[1]=0,假设next[j]=k,下面来推next[j+1]的值:由等式(3)可知next[j+1]的取值有两种情况。
第一种情况:P[j]=P[k],则P[k+1]就是当P[j+1]与T[i]失配时须重新与T[i]相比较的字符,此时next[j+1]=k+1=next[j]+1,如下:
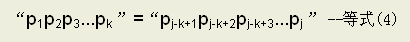
第二种情况:P[j]≠P[k],说明等式(4)不成立,此时应在“p1p2p3...pk”中寻找新的位置k=k’(1<k’<k),使之满足等式(4)。此时求k’的过程也变成了模式匹配的过程,只不过整个模式串P既是主串又是模式串。所以当P[j]≠P[k]时应有k=next[k],再比较此时的P[j]与P[k],若相等则转到第一种情况,此时next[j+1]=next[k]+1=next[next[j]]+1,若k仍不满足等式(4)则继续令k=next[k]……重复以上过程直到找到某个k’(1<k’<j)使得匹配成功或者k’=0,说明不存在这样的子串,此时next[j+1]=1。如下所示:

下面给出求next[]的算法,将会看到该算法形式上与KMP算法神似:
 //
预处理程序,求数组next[] 的值
//
预处理程序,求数组next[] 的值

 void
get_next(
string
P,
int
next[])
{
void
get_next(
string
P,
int
next[])
{ //求模式串P的next数组值,存入next[]中
//求模式串P的next数组值,存入next[]中 i = 1; next[1]=0; j=0;
i = 1; next[1]=0; j=0; while (i < P.length)
while (i < P.length)
 if (j == 0 || P[i] == P[j]) {
if (j == 0 || P[i] == P[j]) { ++i;
++i; ++j;
++j; next[i] = j;
next[i] = j; } else j = next[j];
} else j = next[j]; }
//
get_next
}
//
get_next
依照KMP算法时间复杂度的求法,我们同样可以求出该算法的时间复杂度为O(n)。使用KMP算法进行匹配时,一个模式串在求出它的next值后可与不同的主串进行模式匹配(预处理的好处),并且主串的指针i在匹配过程中不需要回退。该算法在某些情况下比朴素算法效率要高出许多,举个极端的例子:主串由一大堆的0组成,模式串也是一串0但结尾是一个1。尽管朴素算法的时间复杂度是O(m*n),但一般情况下它的复杂度近似为O(n),这是因为在某轮匹配时一般P[j]很快就会与T[i]失配,从而继续下一轮匹配,j不会取遍1至m。所以这种算法仍被广泛地采用,例如标准C库中的字符串匹配函数strstr(),其采用的就是朴素匹配算法。
但上面这个求next[]数组值的算法在某些情况下尚有缺陷,每次对next[j]进行赋值时,并没有考虑P[j+1]=P[k+1]的情况。书上在这里给出的例子很能说明问题:

当T[4]与P[4]失配时,按照next[j]的值则还应该比较T[4]与P[3]、T[4]与P[2]、T[4]与P[1]。但实际上P[4]=P[3]=P[2],所以这三次比较是不需要的,可以直接i++,继续进行T[5]与P[1]的比较。也就是说,如果在求next[j+1]的过程中找到了一个k’(1<k’<j)且P[j+1]=P[k’+1],则说明当P[j+1]与主串失配时P[k’+1]不必再与主串比较了,而应直接和P[next[k’+1]]进行比较,即此时的next[j+1]=next[k’+1]。由此可得到如下求next的改进算法:
 //
预处理程序,求数组next[] 的值的改进算法
//
预处理程序,求数组next[] 的值的改进算法

 void
get_next(
string
P,
int
next[])
{
void
get_next(
string
P,
int
next[])
{ //求模式串P的next数组值,存入next[]中
//求模式串P的next数组值,存入next[]中 i = 1; next[1]=0; j=0;
i = 1; next[1]=0; j=0; while (i < P.length)
while (i < P.length)
 if (j == 0 || P[i] == P[j]) {
if (j == 0 || P[i] == P[j]) { ++i;
++i; ++j;
++j; if (P[i] != P[j])
if (P[i] != P[j]) next[i] = j;
next[i] = j; else
else  next[i] = next[j];
next[i] = next[j]; } else j = next[j];
} else j = next[j]; }
//
get_next
}
//
get_next
总结一下,KMP模式匹配算法由两部分组成,主算法的时间复杂度是O(n),求next的是O(m) (预处理过程),总时间复杂度是O(m+n)。该算法使用了预处理的方法来提高搜索速度,事实上,许多模式匹配算法都巧妙地运用了预处理,从而可以在线性的时间里解决字符串的匹配。每种算法都各具特点,比如BM(Boyer Moore)算法的查找是跳跃式进行的、ASS(Alpha Skip Search)具有亚线性的时间复杂度,还有后缀树,自动机等等。实际选用哪种算法应该具体情况具体分析,其他算法以后学到再说,呵呵~
部分内容及参考源自一下链接:
《Knuth-Morris_Pratt string matching》http://www.ics.uci.edu/~eppstein/161/960227.html






















 658
658

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








