先简单介绍一下概念。设一个m行n列的矩阵具有n个值不等于零的元素,则称t/(m*n)为该矩阵的稀疏因子。通常称稀疏因子小于0.5的矩阵为稀疏矩阵(sparse matrix)。
由于零元素较多,再使用通常的2维数组表示会造成存储空间的浪费,同时在计算时所有零元也要参与运算,导致效率很低。所以有必要研究如何存储稀疏矩阵,即压缩存储。书上这里介绍了3种存储方式,其实第二种行链接的方式是顺序存储的改进方法,二者可以归到一起。由于前两种存储方式实现起来非常简单,书上讲得很细,这里就不啰嗦了,下面主要介绍第三种实现:十字链表。
十字链表是这样构成的:用链表模拟矩阵的行(或者列,这可以根据个人喜好来定),然后再构造代表列的链表,将每一行中的元素节点插入到对应的列中去。打个比方吧:这个十字链表的逻辑结构就像是一个围棋盘(没见过,你就想一下苍蝇拍,这个总见过吧),而非零元就好像是在棋盘上放的棋子,总共占的空间就是,确定那些线的表头节点和那些棋子代表的非零元节点。最后,我们用一个指针指向这个棋盘,这个指针就代表了这个稀疏矩阵。
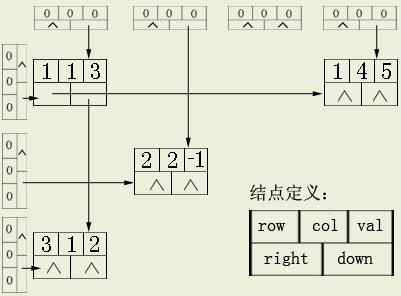
现在,让我们看看非零元节点最少需要哪几个域,val是必须的,为了把线画下去还要有down、right,好像不需要别的了。但为了提高加法与乘法的效率,还要在每个节点增加两个值row,col分别表示节点所在的行、列。再看看表头节点,由于是链表的表头节点,所以就和后边的节点一样了。然后,行链表和列链表的表头节点实际上也各构成了一个链表。最后,我们只需要存储两个分别指向行表头与列表头节点的指针,就可以访问稀疏矩阵了。具体表示如下图:
为了能随机访问任意一行或一列,这里将头结点存放在一维数组中。下面是节点的定义:
class
OLNode {
public :
int row,col,val;
OLNode * right;
OLNode * down;
OLNode( int i = 0 , int j = 0 , int v = 0 ,
OLNode * rgt = NULL, OLNode * dwn = NULL)
: row(i), col(j), val(v), right(rgt), down(dwn) {}
friend std::ostream & operator << (std::ostream & os,
OLNode & eom)
{
os << " ( " << eom.row << " , " << eom.col
<< " , " << eom.val << " ) " ;
return os;
}
};
public :
int row,col,val;
OLNode * right;
OLNode * down;
OLNode( int i = 0 , int j = 0 , int v = 0 ,
OLNode * rgt = NULL, OLNode * dwn = NULL)
: row(i), col(j), val(v), right(rgt), down(dwn) {}
friend std::ostream & operator << (std::ostream & os,
OLNode & eom)
{
os << " ( " << eom.row << " , " << eom.col
<< " , " << eom.val << " ) " ;
return os;
}
};
下边会依次介绍矩阵的转置、加法和乘法,但在这之前先来设计一下类的输出输出接口,一个好的接口能为接下来的运算提供许多方便。除了通常的重载>>与<<之外,为了乘法实现的简便还需要重载=,这在下面会看到:
class
SMatrix_OL {
int maxRows, maxCols, total;
OLNode * pRowHead;
OLNode * pColHead;
void initialize() {
maxRows = maxCols = total = 0 ;
pRowHead = pColHead = NULL;
}
void clear();
void copy( const SMatrix_OL & sm);
friend const SMatrix_OL
vectorMultiply(OLNode * colVector, OLNode * rowVector,
int rows, int cols);
public :
SMatrix_OL() { initialize(); }
// 初始化一个i行j列的零矩阵
SMatrix_OL( int i, int j) {
require(i > 0 && j > 0 ,
" SMatrix_OL::SMatrix illegal matrix! " );
maxRows = i;
maxCols = j;
total = 0 ;
pRowHead = new OLNode[maxRows + 1 ];
pColHead = new OLNode[maxCols + 1 ];
}
SMatrix_OL( const SMatrix_OL & sm) {
copy(sm);
}
SMatrix_OL & operator = ( const SMatrix_OL & sm) {
if (maxRows) clear();
copy(sm);
return * this ;
}
~ SMatrix_OL() {
clear();
}
friend std::ostream & operator << (std::ostream & os,
const SMatrix_OL & sm) {
for ( int i = 1 ; i <= sm.maxRows; i ++ ) {
OLNode * p = sm.pRowHead[i].right;
if (i == 1 )
os << " / " ;
else if (i == sm.maxRows)
os << " / " ;
else os << " | " ;
for ( int j = 1 ; j <= sm.maxCols; j ++ ) {
int val;
if (p == NULL || p -> col > j)
val = 0 ;
else {
val = p -> val;
p = p -> right;
}
os.setf(std::ios::right, std::ios::adjustfield);
os.width( 4 );
os << val;
}
os.setf(std::ios::right, std::ios::adjustfield);
os.width( 4 );
if (i == 1 )
os << " / " ;
else if (i == sm.maxRows)
os << " / " ;
else os << " | " ;
os << std::endl;
}
return os;
}
friend std::istream & operator >> (std::istream & is ,
SMatrix_OL & sm) {
cout << " 创建稀疏矩阵: " << endl;
cout << " 输入行数、列数和非零元个数: " << endl;
is >> sm.maxRows >> sm.maxCols >> sm.total;
require(sm.maxRows > 0 && sm.maxCols > 0 && sm.total >= 0 ,
" SMatrix_OL::operator>> illegal input! " );
sm.pRowHead = new OLNode[sm.maxRows + 1 ];
sm.pColHead = new OLNode[sm.maxCols + 1 ];
for ( int n = 1 ; n <= sm.total; n ++ ) {
cout << " 输入第 " << n << " 个非零元: " << endl;
int i, j, val;
is >> i >> j >> val;
require(i > 0 && j > 0 ,
" SMatrix_OL::operator>> illegal input! " );
OLNode * pNew = new OLNode(i, j, val);
OLNode * prior = & sm.pRowHead[i];
while (prior -> right != NULL && prior -> right -> col < j)
prior = prior -> right;
pNew -> right = prior -> right;
prior -> right = pNew; // 行链接完毕
prior = & sm.pColHead[j];
while (prior -> down != NULL && prior -> down -> row < i)
prior = prior -> down;
pNew -> down = prior -> down;
prior -> down = pNew; // 列链接完毕
}
cout << " 稀疏矩阵创建完毕! " << endl;
return is ;
}
};
void SMatrix_OL::clear() {
for ( int i = 1 ; i <= maxRows; i ++ ) {
if (pRowHead[i].right == NULL) continue ;
OLNode * p = pRowHead[i].right;
// 删除当前行的所有结点
while (p != NULL) {
OLNode * q = p;
p = p -> right;
delete q;
}
}
delete []pRowHead;
delete []pColHead;
}
void SMatrix_OL::copy( const SMatrix_OL & sm) {
maxCols = sm.maxCols;
maxRows = sm.maxRows;
total = sm.total;
pRowHead = new OLNode[maxRows + 1 ];
pColHead = new OLNode[maxCols + 1 ];
OLNode ** pUpNode = new OLNode * [maxCols + 1 ];
for ( int n = 1 ; n <= maxCols; n ++ )
pUpNode[n] = & pColHead[n];
for ( int i = 1 ; i <= maxRows; i ++ ) {
if (sm.pRowHead[i].right == NULL) continue ;
OLNode * prior = & pRowHead[i];
OLNode * pOld = sm.pRowHead[i].right;
while (pOld != NULL) {
OLNode * pCopy = new
OLNode(i, pOld -> col, pOld -> val);
prior = prior -> right = pCopy;
pUpNode[pOld -> col] =
pUpNode[pOld -> col] -> down = pCopy;
pOld = pOld -> right;
}
}
}
int maxRows, maxCols, total;
OLNode * pRowHead;
OLNode * pColHead;
void initialize() {
maxRows = maxCols = total = 0 ;
pRowHead = pColHead = NULL;
}
void clear();
void copy( const SMatrix_OL & sm);
friend const SMatrix_OL
vectorMultiply(OLNode * colVector, OLNode * rowVector,
int rows, int cols);
public :
SMatrix_OL() { initialize(); }
// 初始化一个i行j列的零矩阵
SMatrix_OL( int i, int j) {
require(i > 0 && j > 0 ,
" SMatrix_OL::SMatrix illegal matrix! " );
maxRows = i;
maxCols = j;
total = 0 ;
pRowHead = new OLNode[maxRows + 1 ];
pColHead = new OLNode[maxCols + 1 ];
}
SMatrix_OL( const SMatrix_OL & sm) {
copy(sm);
}
SMatrix_OL & operator = ( const SMatrix_OL & sm) {
if (maxRows) clear();
copy(sm);
return * this ;
}
~ SMatrix_OL() {
clear();
}
friend std::ostream & operator << (std::ostream & os,
const SMatrix_OL & sm) {
for ( int i = 1 ; i <= sm.maxRows; i ++ ) {
OLNode * p = sm.pRowHead[i].right;
if (i == 1 )
os << " / " ;
else if (i == sm.maxRows)
os << " / " ;
else os << " | " ;
for ( int j = 1 ; j <= sm.maxCols; j ++ ) {
int val;
if (p == NULL || p -> col > j)
val = 0 ;
else {
val = p -> val;
p = p -> right;
}
os.setf(std::ios::right, std::ios::adjustfield);
os.width( 4 );
os << val;
}
os.setf(std::ios::right, std::ios::adjustfield);
os.width( 4 );
if (i == 1 )
os << " / " ;
else if (i == sm.maxRows)
os << " / " ;
else os << " | " ;
os << std::endl;
}
return os;
}
friend std::istream & operator >> (std::istream & is ,
SMatrix_OL & sm) {
cout << " 创建稀疏矩阵: " << endl;
cout << " 输入行数、列数和非零元个数: " << endl;
is >> sm.maxRows >> sm.maxCols >> sm.total;
require(sm.maxRows > 0 && sm.maxCols > 0 && sm.total >= 0 ,
" SMatrix_OL::operator>> illegal input! " );
sm.pRowHead = new OLNode[sm.maxRows + 1 ];
sm.pColHead = new OLNode[sm.maxCols + 1 ];
for ( int n = 1 ; n <= sm.total; n ++ ) {
cout << " 输入第 " << n << " 个非零元: " << endl;
int i, j, val;
is >> i >> j >> val;
require(i > 0 && j > 0 ,
" SMatrix_OL::operator>> illegal input! " );
OLNode * pNew = new OLNode(i, j, val);
OLNode * prior = & sm.pRowHead[i];
while (prior -> right != NULL && prior -> right -> col < j)
prior = prior -> right;
pNew -> right = prior -> right;
prior -> right = pNew; // 行链接完毕
prior = & sm.pColHead[j];
while (prior -> down != NULL && prior -> down -> row < i)
prior = prior -> down;
pNew -> down = prior -> down;
prior -> down = pNew; // 列链接完毕
}
cout << " 稀疏矩阵创建完毕! " << endl;
return is ;
}
};
void SMatrix_OL::clear() {
for ( int i = 1 ; i <= maxRows; i ++ ) {
if (pRowHead[i].right == NULL) continue ;
OLNode * p = pRowHead[i].right;
// 删除当前行的所有结点
while (p != NULL) {
OLNode * q = p;
p = p -> right;
delete q;
}
}
delete []pRowHead;
delete []pColHead;
}
void SMatrix_OL::copy( const SMatrix_OL & sm) {
maxCols = sm.maxCols;
maxRows = sm.maxRows;
total = sm.total;
pRowHead = new OLNode[maxRows + 1 ];
pColHead = new OLNode[maxCols + 1 ];
OLNode ** pUpNode = new OLNode * [maxCols + 1 ];
for ( int n = 1 ; n <= maxCols; n ++ )
pUpNode[n] = & pColHead[n];
for ( int i = 1 ; i <= maxRows; i ++ ) {
if (sm.pRowHead[i].right == NULL) continue ;
OLNode * prior = & pRowHead[i];
OLNode * pOld = sm.pRowHead[i].right;
while (pOld != NULL) {
OLNode * pCopy = new
OLNode(i, pOld -> col, pOld -> val);
prior = prior -> right = pCopy;
pUpNode[pOld -> col] =
pUpNode[pOld -> col] -> down = pCopy;
pOld = pOld -> right;
}
}
}
这些都是很常规的实现,不再细说了。首先是转置运算,如果按照一般的方法需要在转置的同时改动很多指针的指向,比较麻烦,这里使用的方式是先把矩阵复制一个临时副本,然后清除原来的矩阵,再以列序从副本复制回来,则现在的矩阵就是原来的转置。代码如下:
//
先把自己复制给sm,然后把自己构造成sm的转置
void Transpose() {
SMatrix_OL sm = * this ;
clear();
maxRows = sm.maxCols;
maxCols = sm.maxRows;
total = sm.total;
pRowHead = new OLNode[maxRows + 1 ];
pColHead = new OLNode[maxCols + 1 ];
OLNode ** pUpNode = new OLNode * [maxCols + 1 ];
for ( int n = 1 ; n <= maxCols; n ++ )
pUpNode[n] = & pColHead[n];
for ( int j = 1 ; j <= sm.maxCols; j ++ ) {
if (sm.pColHead[j].down == NULL) continue ;
OLNode * prior = & pRowHead[j];
OLNode * pOld = sm.pColHead[j].down;
while (pOld != NULL) {
OLNode * pNew = new OLNode(j, pOld -> row, pOld -> val);
prior = prior -> right = pNew;
pUpNode[pNew -> col] =
pUpNode[pNew -> col] -> down = pNew;
pOld = pOld -> down;
}
}
}
const SMatrix_OL operator ~ () {
SMatrix_OL sm = * this ;
sm.Transpose();
return SMatrix_OL(sm);
}
friend const SMatrix_OL
operator + ( const SMatrix_OL & smA, const SMatrix_OL & smB) {
require(smA.maxRows == smB.maxRows &&
smA.maxCols == smB.maxCols,
" SMatrix_OL::operator+ cannot add! " );
SMatrix_OL smC = smA;
smC.Add(smB);
return SMatrix_OL(smC);
}
void Transpose() {
SMatrix_OL sm = * this ;
clear();
maxRows = sm.maxCols;
maxCols = sm.maxRows;
total = sm.total;
pRowHead = new OLNode[maxRows + 1 ];
pColHead = new OLNode[maxCols + 1 ];
OLNode ** pUpNode = new OLNode * [maxCols + 1 ];
for ( int n = 1 ; n <= maxCols; n ++ )
pUpNode[n] = & pColHead[n];
for ( int j = 1 ; j <= sm.maxCols; j ++ ) {
if (sm.pColHead[j].down == NULL) continue ;
OLNode * prior = & pRowHead[j];
OLNode * pOld = sm.pColHead[j].down;
while (pOld != NULL) {
OLNode * pNew = new OLNode(j, pOld -> row, pOld -> val);
prior = prior -> right = pNew;
pUpNode[pNew -> col] =
pUpNode[pNew -> col] -> down = pNew;
pOld = pOld -> down;
}
}
}
const SMatrix_OL operator ~ () {
SMatrix_OL sm = * this ;
sm.Transpose();
return SMatrix_OL(sm);
}
friend const SMatrix_OL
operator + ( const SMatrix_OL & smA, const SMatrix_OL & smB) {
require(smA.maxRows == smB.maxRows &&
smA.maxCols == smB.maxCols,
" SMatrix_OL::operator+ cannot add! " );
SMatrix_OL smC = smA;
smC.Add(smB);
return SMatrix_OL(smC);
}
OK
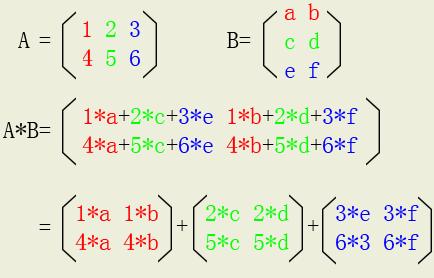
,该本篇文章的压轴算法出场了^_^那就是乘法,书上根本就没有提到十字链表的乘法,原因就是太麻烦了。你想啊,每个节点有两个指针域,而且在做乘法运算时一个矩阵是按行访问,另一个是按列访问,乘积矩阵中的每一个元素都是一行与一列的乘积。我做到这里时头都大了,于是我又想能不能换一种方式:如果矩阵A是行矢量,矩阵B是列矢量,那么A*B很好实现。而一个普通的矩阵可以分解成由子矩阵组成的矢量,所以把A变成行矢量,把B变成列矢量,那么乘积矩阵可由n个子矩阵相加组成,其中n等于A的列数(或B的行数)。见下图:
这样一来,乘法就容易实现了:
friend
const
SMatrix_OL
operator * ( const SMatrix_OL & smA, const SMatrix_OL & smB) {
require(smA.maxCols == smB.maxRows,
" SMatrix_OL operator* cannot mult! " );
SMatrix_OL smC(smA.maxRows, smB.maxCols);
// smC = A1*B1+A2*B2+...+An*Bn,n=smA.maxCols=smB.maxRows
for ( int n = 1 ; n <= smA.maxCols; n ++ )
smC.Add(
vectorMultiply(
smA.pColHead[n].down,
smB.pRowHead[n].right,
smA.maxRows, smB.maxCols));
return SMatrix_OL(smC);
}
operator * ( const SMatrix_OL & smA, const SMatrix_OL & smB) {
require(smA.maxCols == smB.maxRows,
" SMatrix_OL operator* cannot mult! " );
SMatrix_OL smC(smA.maxRows, smB.maxCols);
// smC = A1*B1+A2*B2+...+An*Bn,n=smA.maxCols=smB.maxRows
for ( int n = 1 ; n <= smA.maxCols; n ++ )
smC.Add(
vectorMultiply(
smA.pColHead[n].down,
smB.pRowHead[n].right,
smA.maxRows, smB.maxCols));
return SMatrix_OL(smC);
}
其中的核心就是私有成员函数vectorMultiply,将两个矢量相乘,其实现也很简单:
const
SMatrix_OL
vectorMultiply(OLNode * colVector,
OLNode * rowVector, int rows, int cols)
{
SMatrix_OL sm(rows, cols);
if (colVector != NULL && rowVector != NULL) {
OLNode ** pUpNode = new OLNode * [sm.maxCols + 1 ];
for ( int n = 1 ; n <= sm.maxCols; n ++ )
pUpNode[n] = & sm.pColHead[n];
// 行、列矢量相乘
for (; colVector != NULL; colVector = colVector -> down) {
OLNode * prior = & sm.pRowHead[colVector -> row];
for (OLNode * pCur = rowVector;
pCur != NULL; pCur = pCur -> right)
{
OLNode * pNew = new
OLNode(colVector -> row,
pCur -> col, colVector -> val * pCur -> val);
prior = prior -> right = pNew;
pUpNode[pNew -> col] =
pUpNode[pNew -> col] -> down = pNew;
sm.total ++ ;
}
}
}
return SMatrix_OL(sm);
}
vectorMultiply(OLNode * colVector,
OLNode * rowVector, int rows, int cols)
{
SMatrix_OL sm(rows, cols);
if (colVector != NULL && rowVector != NULL) {
OLNode ** pUpNode = new OLNode * [sm.maxCols + 1 ];
for ( int n = 1 ; n <= sm.maxCols; n ++ )
pUpNode[n] = & sm.pColHead[n];
// 行、列矢量相乘
for (; colVector != NULL; colVector = colVector -> down) {
OLNode * prior = & sm.pRowHead[colVector -> row];
for (OLNode * pCur = rowVector;
pCur != NULL; pCur = pCur -> right)
{
OLNode * pNew = new
OLNode(colVector -> row,
pCur -> col, colVector -> val * pCur -> val);
prior = prior -> right = pNew;
pUpNode[pNew -> col] =
pUpNode[pNew -> col] -> down = pNew;
sm.total ++ ;
}
}
}
return SMatrix_OL(sm);
}
下面该测试了,这里同样使用了sstream文件,其功能在上一篇文章已经说过了。
#include
"
SMatrix.h
"
#include < iostream >
#include < sstream >
using namespace std;
int main() {
stringstream input( "
3 2 6
1 1 1 1 2 2 2 1 3 2 2 4 3 1 5 3 2 6
" );
SMatrix_OL A;
input >> A;
cout << " A = " << endl << A;
SMatrix_OL B = A;
cout << " B = " << endl << B;
cout << " A + B = " << endl << A + B;
cout << " B's transpose matrix = " << endl << ~ B;
cout << " A * ~B = " << endl << A * ~ B;
return 0 ;
}
#include < iostream >
#include < sstream >
using namespace std;
int main() {
stringstream input( "
3 2 6
1 1 1 1 2 2 2 1 3 2 2 4 3 1 5 3 2 6
" );
SMatrix_OL A;
input >> A;
cout << " A = " << endl << A;
SMatrix_OL B = A;
cout << " B = " << endl << B;
cout << " A + B = " << endl << A + B;
cout << " B's transpose matrix = " << endl << ~ B;
cout << " A * ~B = " << endl << A * ~ B;
return 0 ;
}
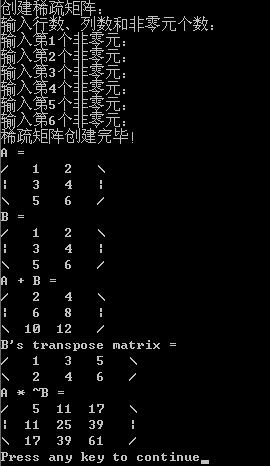
可以看出,重载了一些符号之后使得矩阵的运算与内部类型就很相似了,下面是运行结果:
好了,第五章到此就结束了。本来后面还有广义表,但由于最近时间比较紧张就不打算再写了。这篇文章也是很匆忙地写完的,总觉得有些仓促,以后有时间会再修改一下,毕竟十字链表不比前几章学过的线性表,在实现上要复杂一些,包括下一节的广义表也是。虽然这部分内容不是重点,但我觉得系统地学习一下还是有好处的,可以为后面学习树打下基础,因为树的大部分运算都是递归的,并且其中的二叉树与十字链表一样有两个指针域。下一篇开始介绍第六章--树,也就是数据结构这门课程最重要的章节~预计分3篇文章,如果时间足够的话可能会把广义表补上,但广义表我又是在想不出一个好的应用,只写基本操作也没什么意思,到时候再说吧,呵呵~
最后说几句题外话,最近忙主要是因为把精力都花在学外语上了。这个星期是我们学校的英语周,从美国来了10多个老外,每天晚上都有讲座或者是娱乐活动。我每天下午都会去找他们聊天,练习口语,感觉这个星期收获很大,刚开始的时候只能一个词一个词的往外蹦,现在进本上能一段一段的说了!并且与一个叫Christ的老头儿交上了朋友,今天我去送得他,还送给他一个自己做得小礼物。老外很有意思,他们和你说话时面部表情特别丰富,还是不是加上许多肢体动作,让人感觉很亲切,呵呵~
























 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








