排序算法（2）——归并排序

归并排序（Merge Sort）

   （1）算法思想

             归并排序采用了分治策略（divide-and-conquer），就是将原问题分解为一些规模较小的相似子问题，然后递归解决这些子问题，最后合并其结果作为原问题的解。

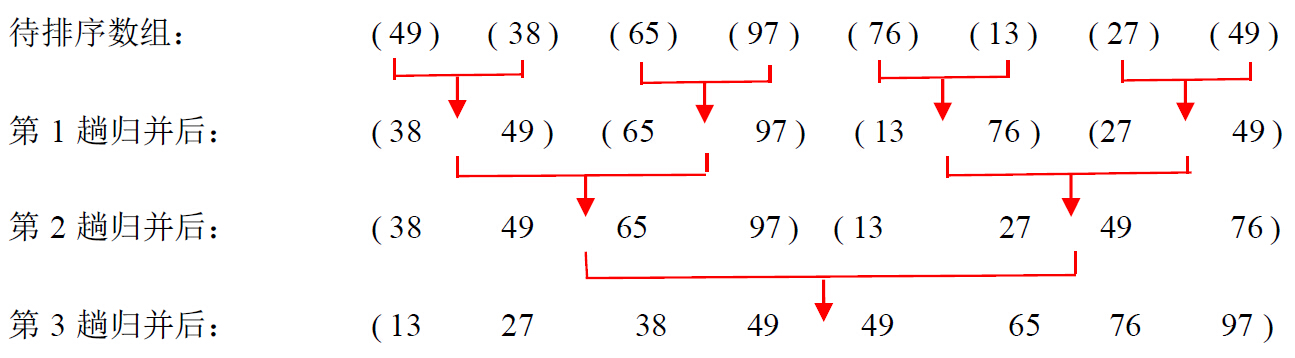
              归并排序将待排序数组A[1..n]分成两个各含n/2个元素的子序列，然后对这个两个子序列进行递归排序，最后将这两个已排序的子序列进行合并，即得到最终排好序的序列。具体排序过程如下图所示：

             归并排序中一个很重要的部分是两个已排序序列合并的过程，这里需要另外开辟一块新的空间来作为存储这两个已排序序列的临时容器。假设对A[p..r]序列进行合并，已知A[p..q]及A[q+1..r]为已排序的序列，合并的具体步骤为：

            Step 1：新建两个数组L、R分别存储待合并序列A[p..q]和A[q+1..r]，将待排序序列中的对应元素copy到L和R中，L和R最后设置一个极大值作为“哨兵”；

           Step 2：令指针i指向L的起始元素，j指向R的起始元素，k指向A待合并部分的起始元素A[p]；

           Step 3：若L[i]≤R[j]，令A[k]=L[i]，i=i+1，k=k+1；

                         否则，令A[k]=R[j]，j=j+1，k=k+1；

                        （这一步即依次比较i、j所指向的元素，将较小值依次放入到A中相应位置。）

          Step 4 ：重复Step 3，r-p+1次后停止，即依次确定A[p..q]每个位置上的元素。

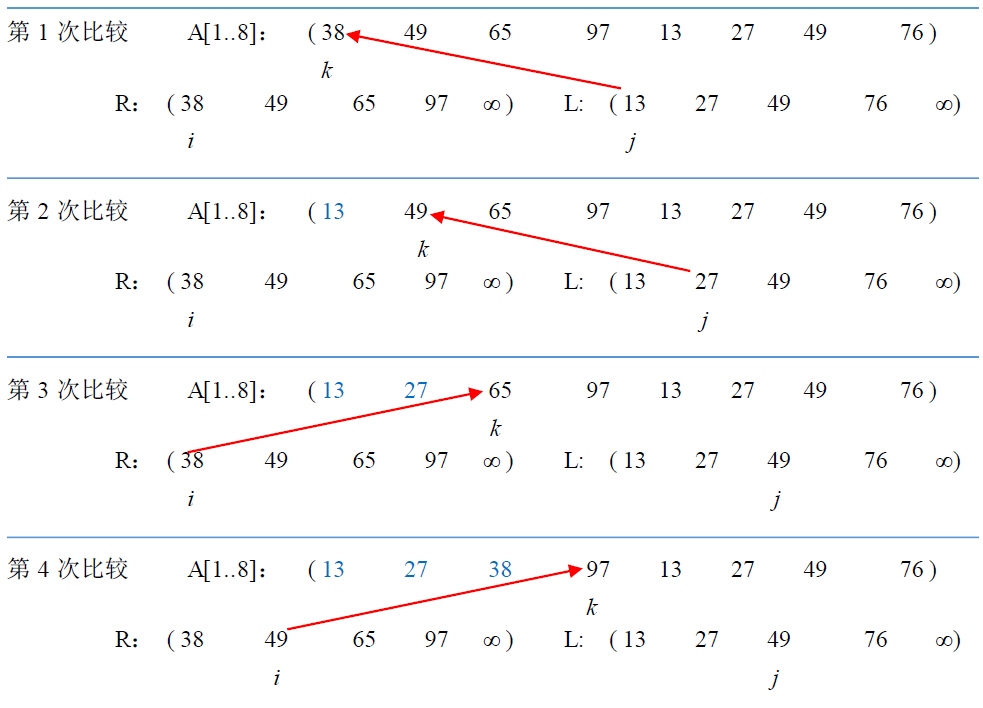
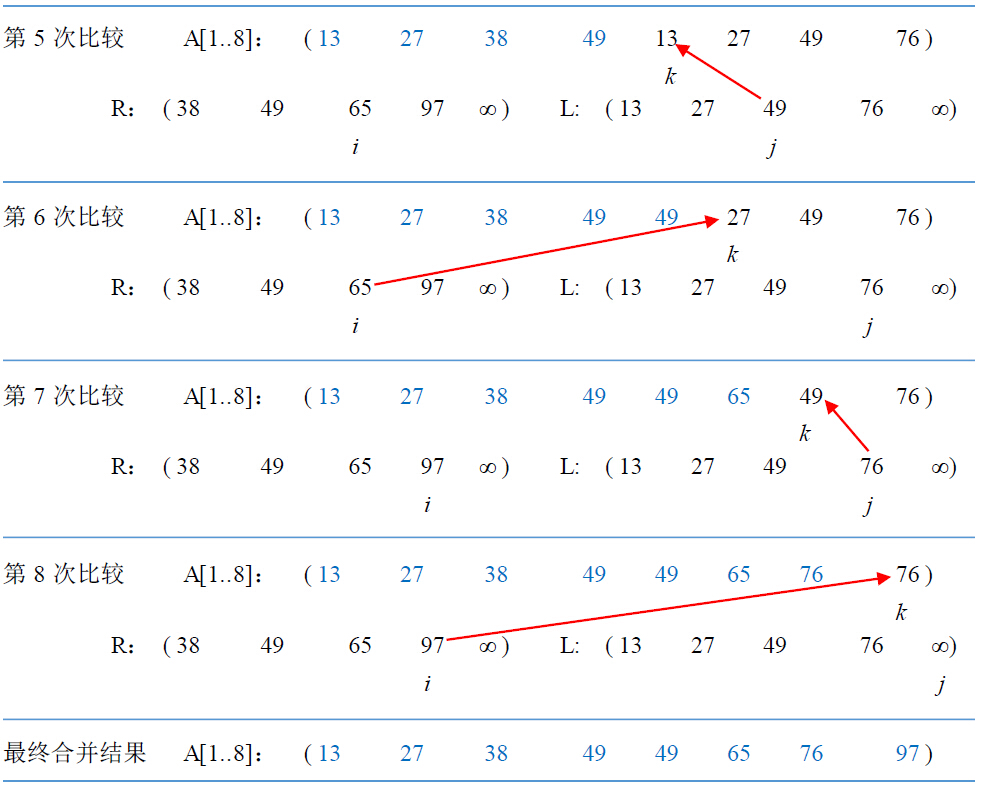
         经过合并操作后，A[p..q]为一个有序序列。若待合并序列为（38， 49， 65， 97， 13， 27， 49， 76），p=1，q=4,， r=8，即A[1..4]和A[5..8]分别为有序序列，则合并操作的具体过程如下图所示：

    （2）伪代码

             MERGE SORT(A, p, r)                                    //对A[p..r]进行归并排序
             1 if  p < r
             2     then q ← ⎣(p+r)/2⎦                                     //将A[p..r]分成两个子序列进行递归归并排序
             3             MERGE-SORT (A, p, q)
             4             MERGE-SORT (A, q+1, r)
             5             MERGE (A, p, q, r)                           //将已排序的两个子序列进行合并

             MERGE(A, p, q, r)
             1 n1 ← q-p+1;                                                  //计算左半部分已排序序列的长度
             2 n2 2 ← r-q;                                                    //计算右半部分已排序序列的长度
             3 create arrays L[1..n1+1] and R[1..n2+1]      //新建两个数组临时存储两个已排序序列，长度+1是因为最后有一个标志位
             4 for i ← 1 to n1
             5      do L[i] ← A[p + i-1]                                //copy左半部分已排序序列到L中
             6 for j ← 1 to n2
             7      do R[j] ← A[q + j]                                   //copy右半部分已排序序列到R中
             8 L[n1+1] ← ∞                                                //L、R最后一位设置一个极大值作为标志位                       
             9 R[n2+1] ← ∞
            10 i ← 1
            11 j ← 1
            12 for k ← p to r                                              //进行合并
            13      do if L[i] < R[j]
            14          then A[k] ← L[i]
            15                  i ← i + 1
            16          else A[k] ← R[j]
            17                  j ← j + 1

          

    （3）代码实现

             注意，开始排序时，p、r表示的是待排序数组的起始下标和终止下标，例如，若A=（38， 49， 65， 97， 13， 27， 49， 76），对A进行排序，调用MergeSort（A, 0, 7），即p=0, r=7.

void Merge(int A[],int p,int q,int r)
{
    int i,j,k;
    int n1=q-p+1;
    int n2=r-q;
    int *L=new int[n1+1]; //开辟临时存储空间
    int *R=new int[n2+1];
    for(i=0;i<n1;i++)
        L[i]=A[i+p];      //数组下标从0开始时，这里为i+p
    for(j=0;j<n2;j++)
        R[j]=A[j+q+1];    //数组下标从0开始时，这里为就j+q+1
    L[n1]=INT_MAX;        //"哨兵"设置为整数的最大值，INT_MAX包含在limits.h头文件中
    R[n2]=INT_MAX;
    i=0;
    j=0;
    for(k=p;k<=r;k++)     //开始合并
    {
        if(L[i]<=R[j])
            A[k]=L[i++];
        else
            A[k]=R[j++];
    }
}

void MergeSort(int A[],int p,int r) 
{
    if(p<r)
    {
        int q=(p+r)/2;
        MergeSort(A,p,q);
        MergeSort(A,q+1,r);
        Merge(A,p,q,r);
    }

              通过简单的变化，L、R也可以不使用“哨兵”，当L中的元素全部填入A中时，后面过程直接将R剩余部分copy到A中；当R中的元素全部填入A中时，后面过程直接将L剩余部分copy到A中。具体实现如下：

void Merge2(int A[],int p,int q,int r)
{
    int i,j,k;
    int n1=q-p+1;
    int n2=r-q;
    int *L=new int[n1]; 
    int *R=new int[n2];
    for(i=0;i<n1;i++)
        L[i]=A[i+p];      
    for(j=0;j<n2;j++)
        R[j]=A[j+q+1];    
    i=0;
    j=0;
    for(k=p;k<=r;k++)     
    {
        if(j==n2||L[i]<=R[j])   //注意：此处加了j==n2的或条件
            A[k]=L[i++];
        else
            A[k]=R[j++];
    }
}

    （4）算法分析

             a.归并排序的时间复杂度为：Θ（nlgn），其中 MERGE(A, p, q, r)的时间复杂度为Θ（n）。

             b.归并排序并不是一种原地排序，因为需要额外申请空间来充当临时容器。

             c.归并排序是一种稳定排序。